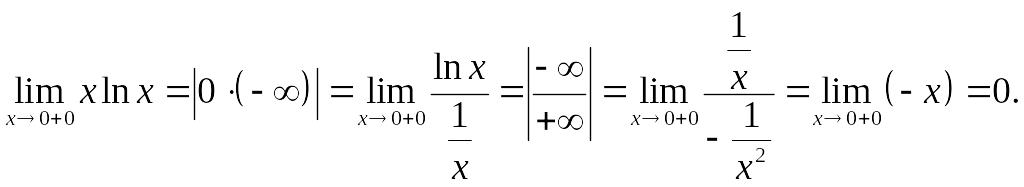6. Вычисление пределов функций с помощью производной. Правило Лопиталя.
В
этом параграфе мы рассмотрим удобный
прием при вычислении сложных пределов.
Будем предполагать в дальнейшем, что
либо число, либо один из символов
 .
.
Определение.
Предел
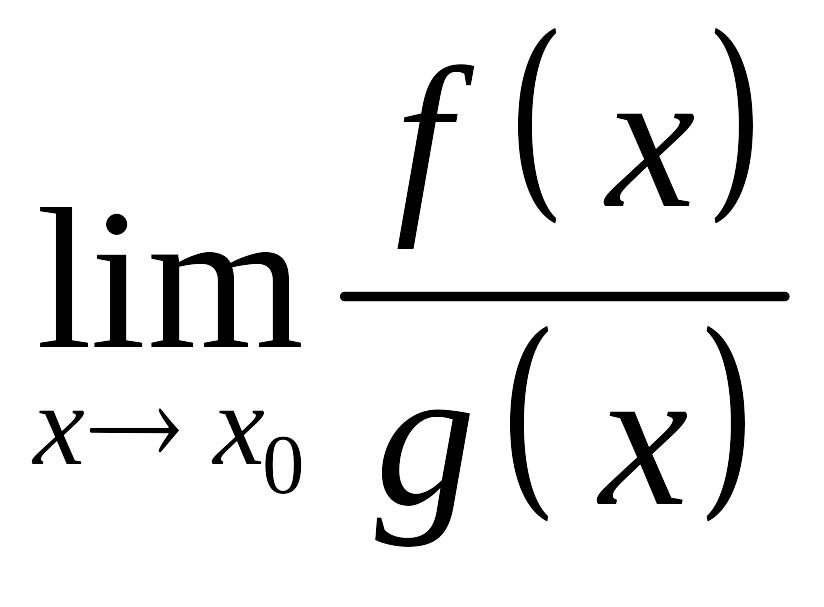 называется неопределенностью вида
называется неопределенностью вида
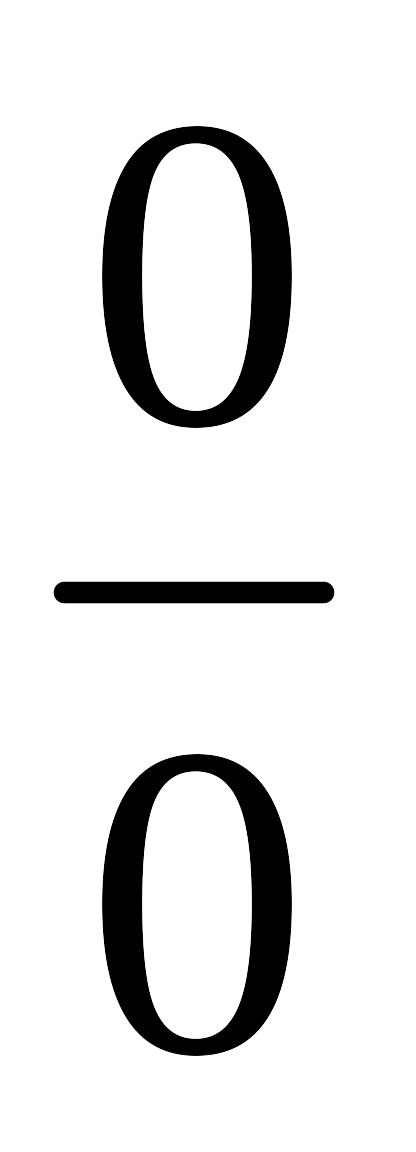 (или
(или
 ),
если существует
),
если существует
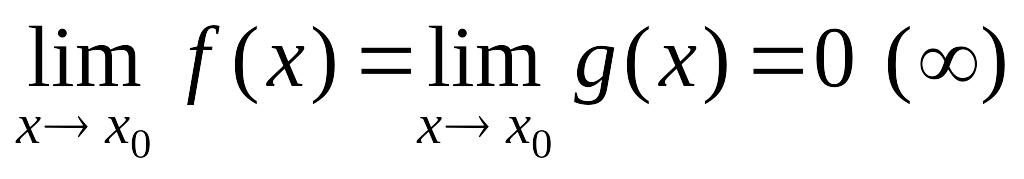 .
Раскрыть неопределенность означает
найти данный предел.
.
Раскрыть неопределенность означает
найти данный предел.
При
раскрытии неопределенностей
и
очень эффективно правило Лопиталя.
Теорема
(Лопиталя). Пусть
функции
и
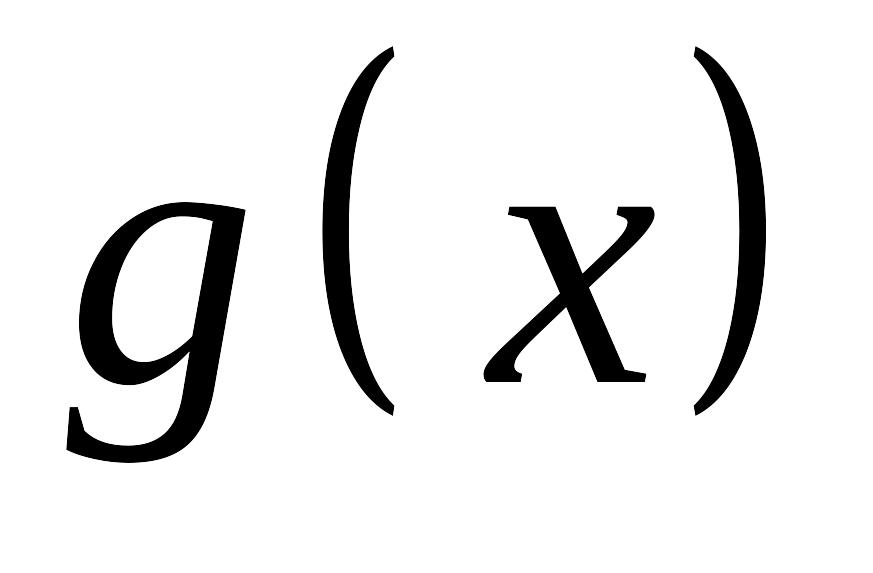 определены и дифференцируемы в
определены и дифференцируемы в
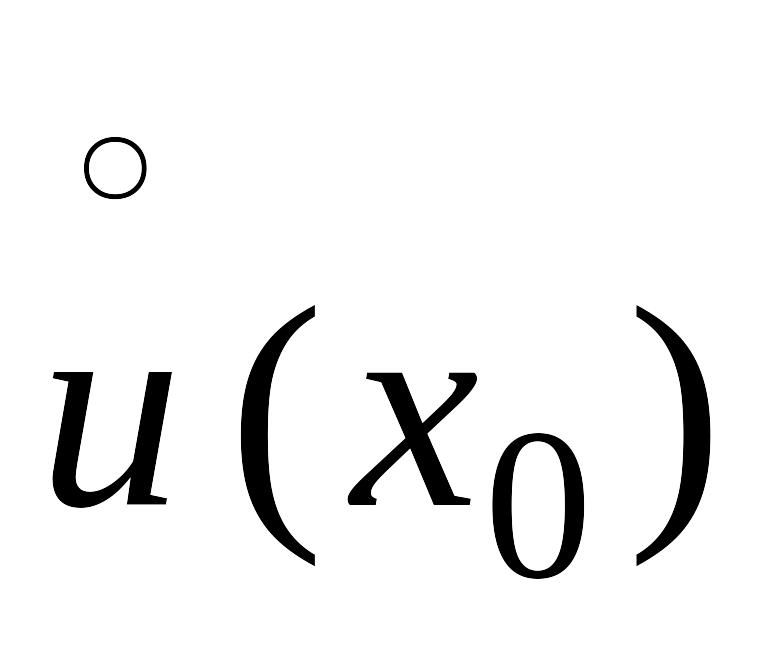 и выполнены условия:
и выполнены условия:
1)
и
либо обе БМФ, либо обе ББФ при
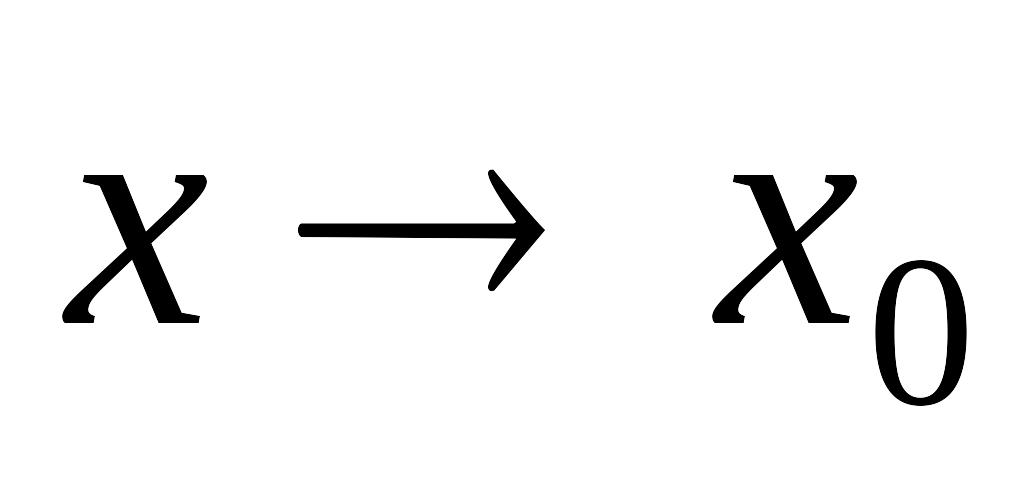 ;
;
2)
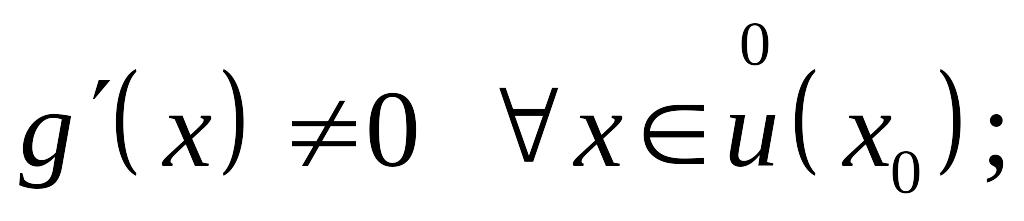
Тогда
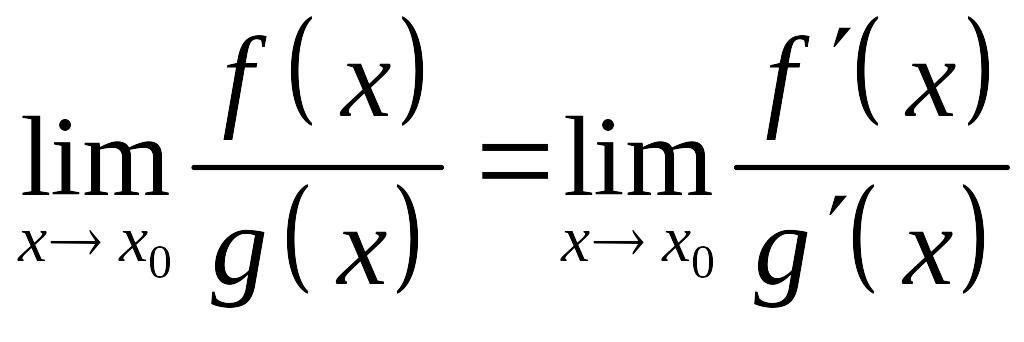 при условии, что предел справа существует.
при условии, что предел справа существует.
Пример
1.

Пример
2.
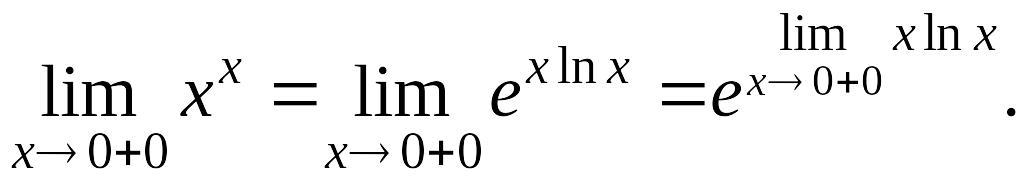
Здесь
мы использовали теорему о переходе к
пределу под знаком непрерывной функции.
Найдем
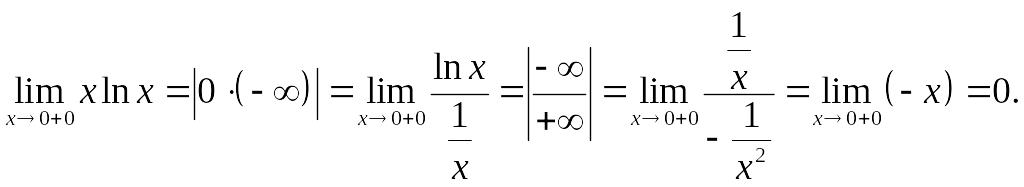
Поэтому
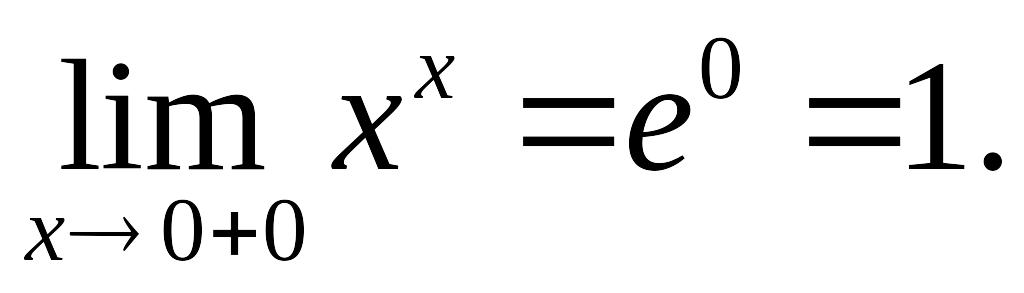


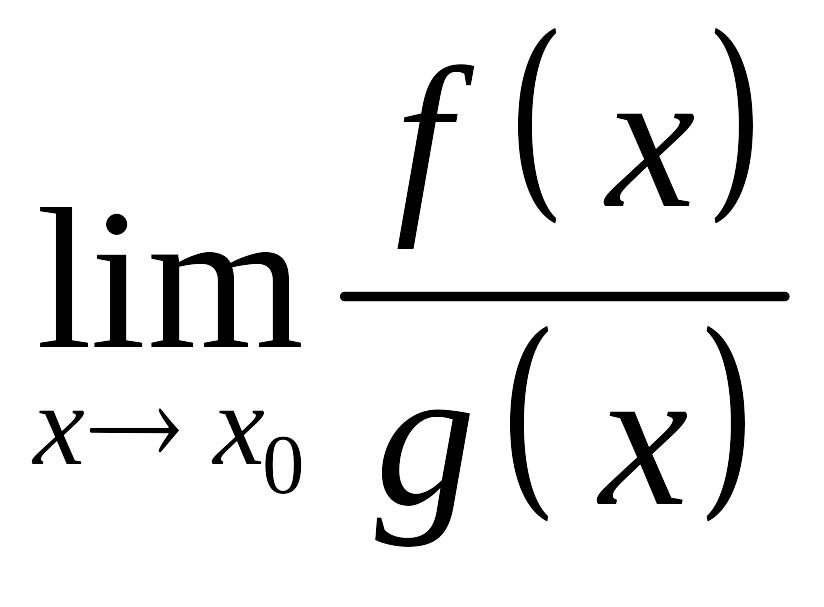 называется неопределенностью вида
называется неопределенностью вида
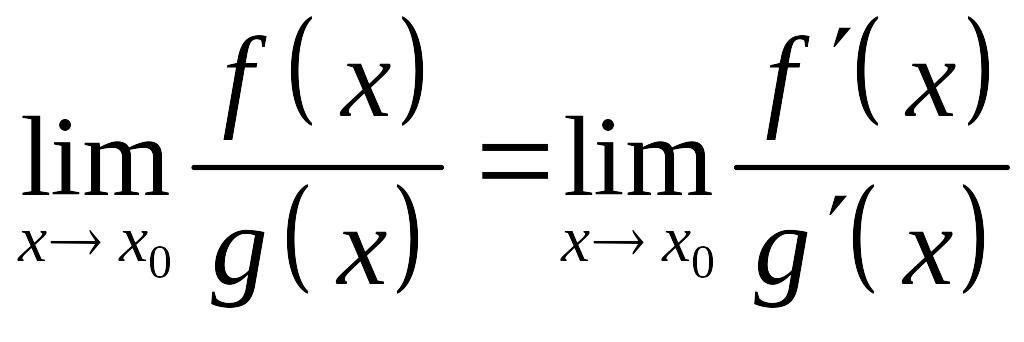 при условии, что предел справа существует.
при условии, что предел справа существует.