Тема: Производная и дифференциал функции одной переменной Производная функции.

1. Определение и свойства.

К понятию производной приводит задача о вычислении мгновенной скорости движущейся материальной точки, задача о вычислении скорости изменения стоимости акций, задача о касательной к кривой и другие задачи.

Определение. Пусть функция определена в . Производной функции называется

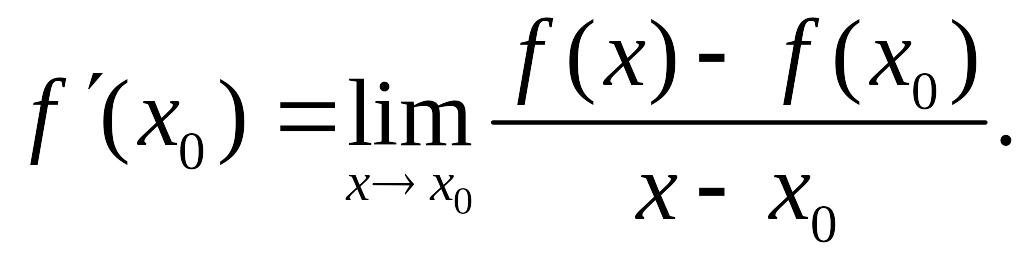(1)

Если предел (1) существует, то функция называется дифференцируемой в точке . В противном случае говорят, что функция не имеет производной в точке или не дифференцируема в точке .

Для обозначения производной используются также символы:

Обозначим и называются приращениями аргумента и функции соответственно. Тогда и при . Поэтому равенство (1) можно переписать так :

.

Определение. Функция называется дифференцируемой на интервале, если она дифференцируема в каждой точке этого интервала.

Сформулируем основные правила дифференцирования.

Пусть и дифференцируемые в точке функции и const. Тогда

1. (производная константы равна 0);

2. ; 4. ;

3. ; 5. ;

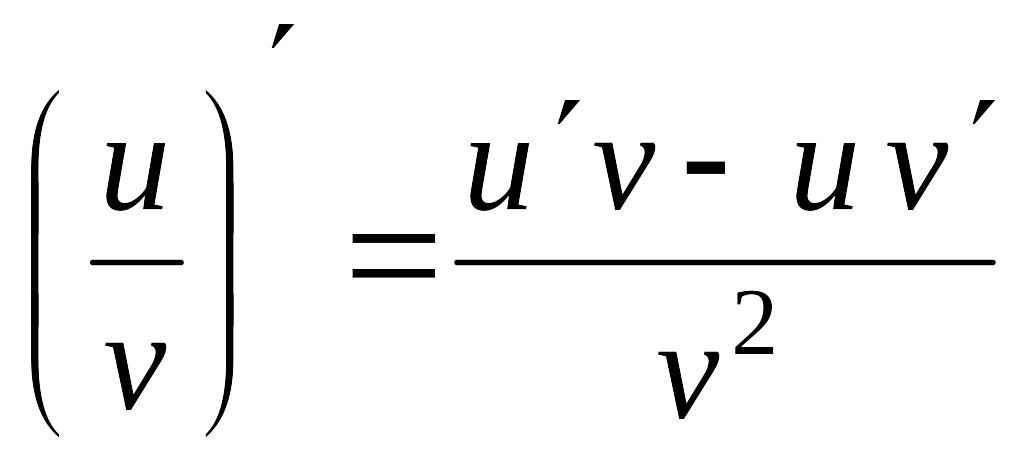6. Правило дифференцирования сложной функции.

Пусть функция дифференцируема в точке , а функция дифференцируема в точке . Тогда сложная функция дифференцируема в точке и

Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.

Приведем таблицу производных основных элементарных функций.

	8. ( tg
	9. (ctg
	;
	12. (arctg
	13. (arcctg

Формулы 1. – 9. данной таблицы получаются из таблицы пределов с помощью правил Например, 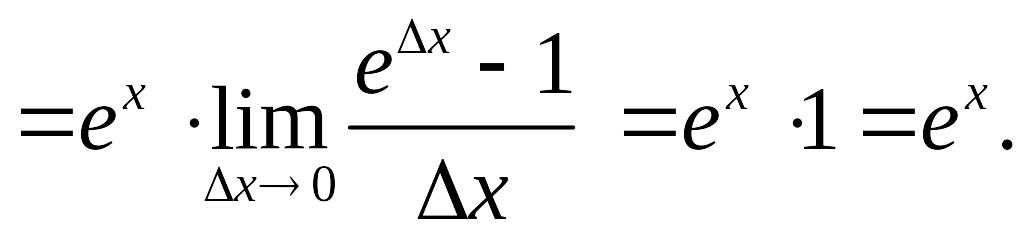Здесь мы использовали формулу 2. таблицы пределов и правило 3.

Используя правила дифференцирования 1.- 6. и таблицу производных можно найти производную любой элементарной функции.

Пример 1.

Пример 2. Пусть . Найти . Выделим у этой сложной функции внешнюю и внутреннюю функции: , где Пользуясь правилом 6, найдем .

Замечание 1. Из предыдущего примера видно, как важно при вычислении производной сложной функции правильно выделить внешнюю и внутреннюю функции.

Замечание 2. Если функция дифференцируема в точке , то непрерывна в точке . Действительно,

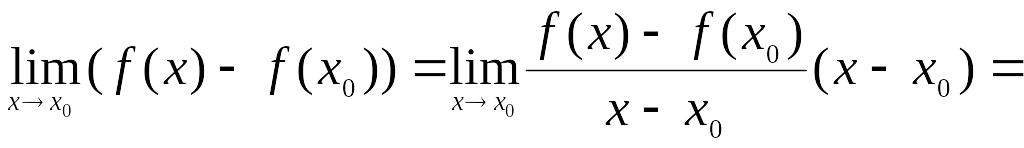
. Обратное неверно. То есть непрерывная в точке функция может не иметь производной в точке . Например, функция непрерывна при всех , но не дифференцируема при

Задача. Доказать, что функция не дифференцируема при

2. Дифференциал функции.

Приращение переменной в точке называют также дифференциалом в точке и обозначают . Таким образом, .

Определение. Пусть функция дифференцируема в точке . Дифференциалом в точке называют выражение

Замечание. Из данного определения и соответствующих свойств производной вытекают следующие свойства дифференциала функции:

1)

2) , где const.

3) , где const.
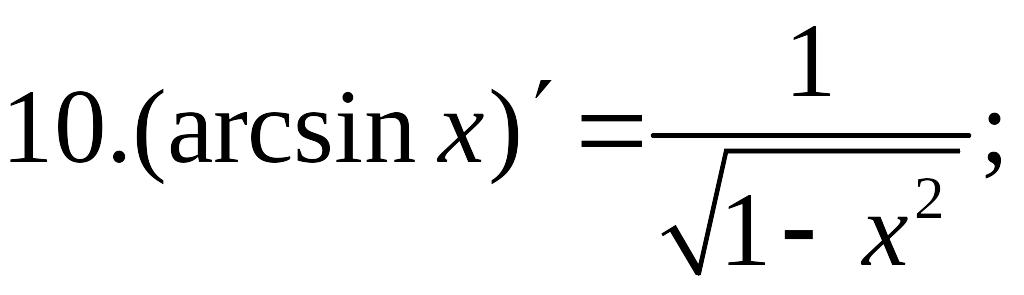
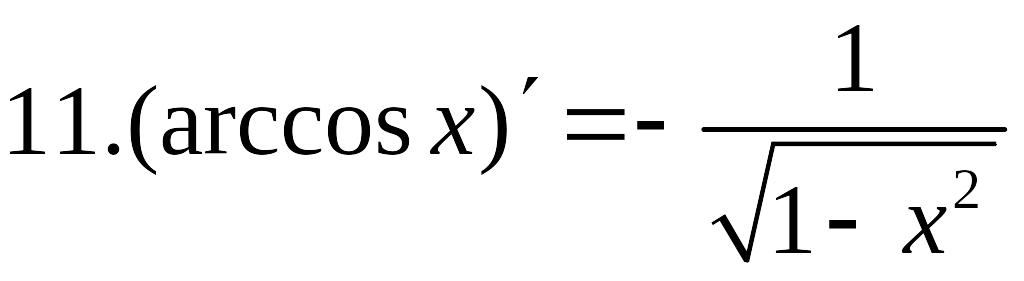