1) Определить, в каком объеме нужно выпускать продукцию для удовлетворения спроса, решив систему линейных уравнений

(Е - А) • X = Р методом Гаусса;

2) Исследовать, как изменится выпуск продукции, решая уравнение

X = (Е – А)^-1 • F₁ как матричное, если спрос на вторую продукцию увеличится на 39 % ;

3 ) Исследовать, как изменится выпуск продукции, решая уравнение

X = (Е - А)^-1 • F₂ как матричное, если спрос на вторую продукцию уменьшится на 27 %.

Алгоритм решения задачи:

1 . Составить модель межотраслевого баланса Леонтьева.

2. Найти матрицу-столбец равновесных объемов производств, решив систему линейных уравнений вида (Е - А) • X =F методом Гаусса.

3. Найти матричный мультипликатор Леонтьева (Е-А)^-1 .

4. Изменить матрицу-столбец спроса, учитывая увеличение спроса на продукцию второй отрасли на 39%, и найти матрицу-столбец объемов производств, решая

систему линейных уравнений как матричное уравнение X=(Е- А)^-1 • F.

5. Определить, на сколько процентов увеличится объем выпуска каждой отрасли при увеличенном спросе на продукцию второй отрасли.

6. Изменить матрицу столбец спроса, учитывая уменьшение спроса на продукцию второй отрасли на 27 %, и найти матрицу-столбец объемов производств, решая

систему линейных уравнений как матричное уравнение X = (Е - А)^-1 •F .

7. Определить, на сколько процентов уменьшится объем выпуска каждой отрасли при уменьшенном спросе на продукцию второй отрасли.

Решение.

1. Запишем модель межотраслевого баланса Леонтьева в виде X=A^.X+F, или

(E-A)^.X=F.

2. Запишем систему (E-A)^.X=F методом Гаусса.

П риведем расширенную матрицу к ступенчатому виду методом элементарных преобразований:

( E-A|F)→

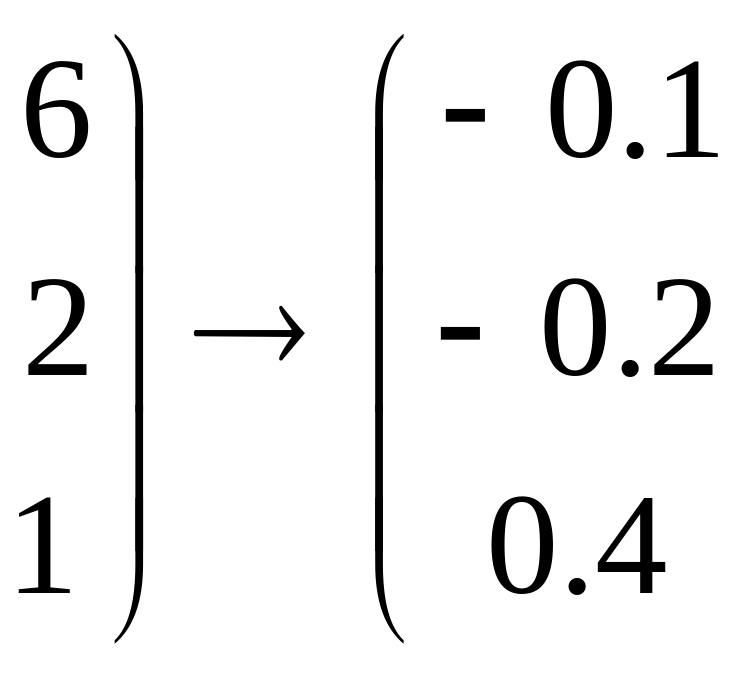
Определим ранги матриц: rg(E-A)=rg(E-A|F)=3. Следовательно, по теореме Кронокера-Капели [1-3] система совместна и имеет единственное решение. Запишем это решение. Для этого выпишем третье уравнение: 0.5х₃=10. Отсюда х₃=20. Выпишем второе уравнение, подставим х₃ и найдем х₂: 0.6х₂-0.9х₃=0

0.6х₂-0.9^.20=0

0.6х₂ -18=0

0.6х₂=18

х₂=18:0.6

х₂=30.

Выпишем первое уравнение и найдем х₁:

-0.1х₁-0.1х₂+0.4х₃=1

-0.1х₁-0.1^.30+0.4^.20=1

-0.1х₁-3+8=1

-0.1х₁=-4

х₁=-4:(-0.1)

х₁=40.

Отсюда получим решение системы: Х=(40 30 20)^Т.

3. Найдем матричный мультипликатор Леонтьева (Е-А)^-1:

(Е-А)=

1) Найдем определитель матрицы =

=0.4³+(-0.2)^.(-0.1)^.(-0.2)+(-0.2)^.(-0.1)^.(-0.1)-(-0.1)^.0.4^.(-0.2)-(-0.1)^.(-0.1)^.0.4-(-0.2)^.(-0.2)^.0.4=

=0.03

2) Транспонируем матрицу: →

3) Находим присоединенную матрицу:

а) Найдем алгебраические дополнения:

А₁₁=0.15

А₁₂=0.09

А₁₃=0.06

А₂₁=0.1

А₂₂=0.14

А₂₃=0.06

А₃₁=0.1

А₃₂=0.08

А₃₃=0.12

б) Составим присоединенную матрицу:

4)найдем обратную матрицу. Для этого поделим каждый элемент присоединенной матрицы на определитель матрицы (Е-А):

(Е-А)^-1=

4. Предположим, что спрос на продукцию 2-й отрасли увеличится на 39 %. Тогда Второй элемент столбца конечного спроса F станет равным 2+2^.0.39=2.78. Решим задачу нахождения объема продукции при увеличении конечного спроса на продукцию второй отрасли.

Приведем расширенную матрицу к ступенчатому виду методом элементарных преобразований:

( E-A|F)→

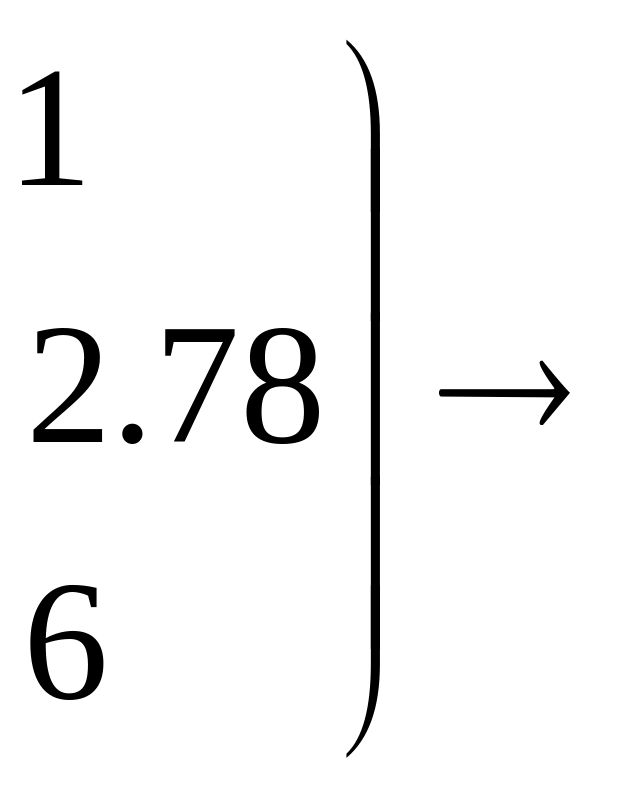
Найдем объемы выпускаемой продукции по формуле Х₁=(Е-А)^-1F₁.Приближенное решение имеет вид:

0.5x₃=10.78

x₃=21.56

0.6x₂-0.9^.21.56=0.78

x₂=33.64

-0.1x₁-0.1^.33.64+0.4^.21.56=1

x₁=42.6

X₁= .

Вывод: увеличение спроса на продукцию второй отрасли на 39 % повлекло за собой увеличение объема выпуска продукции первой отрасли на и третьей отрасли на .

5. Предположим, что спрос на продукцию 2-й отрасли уменьшился на 27 %. Тогда второй элемент столбца конечного спроса F станет равным 2-2^.0.27=1.46. Решим задачу нахождения объема продукции при уменьшении конечного спроса на продукцию 2-й отрасли. Вектор конечного спроса будет иметь вид F₂=(6 1.46 1)^T. Решая полученную систему Х₂=(Е-А)^-1F₂, получаем приближенное решение:

( E-A|F)→

0.5x₃=9.46

x₃=18.92

0.6x₂-0.9^.18.92=-0.54

x₂=27.48

-0.1x₁-0.1^.27.48+0.4^.18.92=1

x₁=38.2

Х₂= .

Анализ результатов показывает, что уменьшение спроса на продукцию второй отрасли на 27% повлекло за собой уменьшение объема выпуска продукции первой отрасли на 4,5% и третьей отрасли на 5,4% соответственно.

Вывод: я убедилась, что благодаря применению систем алгебраических линейных уравнений можно описывать и анализировать модели межотраслевого баланса.