4.4. Ориентированные графы

Ориентированный граф или орграф представляет собой пару G = (V, Е), где V — конечное множество вершин, а Е — отношение на V. Графическое изображение графа состоит из множества помеченных вершин с ориентированными ребрами (называемых дугами), соединяющими пары вершин. Совокупность всех дуг образует множество Е.

Дугу, соединяющую пару (u, v) вершин u и v орграфа G, будем обозначать через uv. В простом орграфе отсутствуют петли и кратные дуги. Следовательно, для любой пары вершин u и v в орграфе найдется не более одной дуги uv из вершины и в v, и не более одной дуги vu из v в и. Если uv — дуга орграфа, то и называют антецедентом v.

На рис. 4.30 приведен пример простого орграфа с множеством вершин V = {а, Ь, с, d} и множеством дуг Е = {ab, bd, cb, db, dc}.

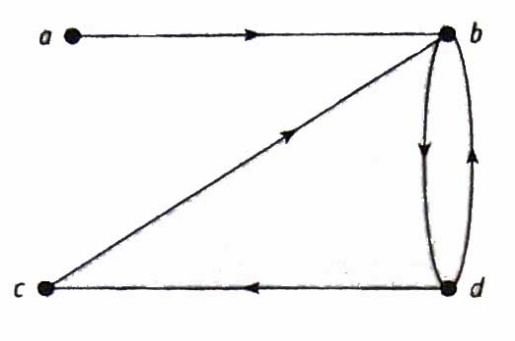
Рис. 4.30. Пример орграфа

Матрицей смежности данного графа служит (несимметричная) матрица:

(вершины а, с и d здесь — антецеденты b).

Путем длины k в орграфе называют последовательность различных вершин v₀, v₁, ..., v_k, каждая пара v_i-1v_i которой образует дугу (i = 1,...,k). Контуром в орграфе G принято называть последовательность вершин v_0, v₁,... v_k, образующую путь, в которой первая вершина v₀ совпадает с последней v_k , а других повторяющихся вершин в ней нет. Орграф G называют бесконтурным, если в нем нет контуров.

Бесконтурные орграфы полезны в качестве моделей ситуаций, задачи в которых должны выполняться в определенном порядке (контур в такой интерпретации означает, что та или иная задача выполняется с некоторой периодичностью и предшествует сама себе). В задаче о планировании заданий соответствующий бесконтурный орграф имеет кодовое название «система ПЕРТ».

Пример 1. Для получения степени магистра биологии студенту университета, в частности, необходимо прослушать восемь курсов, которые некоторым образом зависят друг от друга. Эта зависимость представлена в табл. 4.5. Изобразите систему ПЕРТ, иллюстрирующую приоритетную структуру курсов.

Таблица 4.5

	Предварительные курсы
(A)	Биотехнология	B
(B)	Начальный курс биотехнологии	C
(C)	Цитология	H
(D)	Структура ДНК	C
(E)	Энзимология	D,G
(F)	Диетология	E
(G)	Генная инженерия	C
(H)	Биология человека	Никаких требований

Решение. Система ПЕРТ (см. рис. 4.31) — это просто орграф, представляющий данную приоритетную структуру. Вершины орграфа в данном случае — восемь курсов. Для краткости ссылок мы обозначим курсы буквами латинского алфавита от А до Н. Дуги орграфа отражают представленные в таблице требования, необходимые для усвоения данного курса.

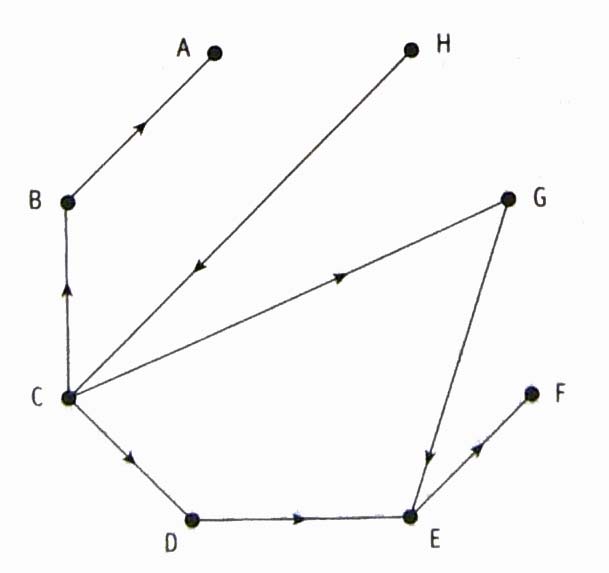
Рис. 4.31 Система ПЕРТ: Приоритетная структура курсов

Предположим, что студент из примера 1 намерен определить порядок, в котором ему следует изучать предметы, учитывая их зависимость друг от друга. Он может сделать это с помощью алгоритма топологической сортировки. Алгоритм создает последовательность согласованных меток для вершин бесконтурного орграфа таким образом, что если 1, 2, 3, ..., п — метки вершин и uv — дуга орграфа, идущая от вершины и с меткой i к вершине v с меткой j, то i < j.