Алгоритм ближайшего соседа

Этот алгоритм выдает субоптимальное решение задачи коммивояжера, генерируя гамильтоновы циклы в нагруженном графе с множеством вершин V. Цикл, полученный в результате работы алгоритма, будет совпадать с конечным значением переменной маршрут, а его общая длина — конечное значение переменной w.

Пример 6. Примените алгоритм ближайшего соседа к графу, изображенному на рис. 4.12. За исходную вершину возьмите вершину D.

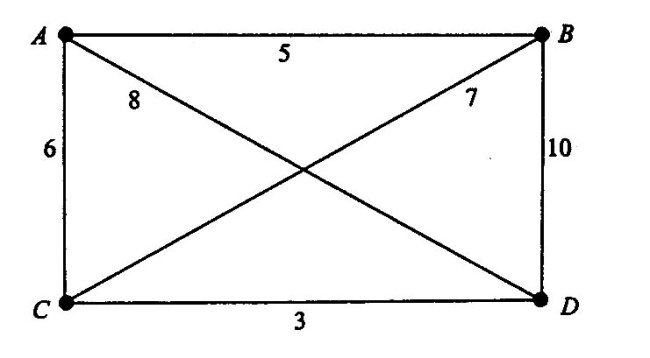
Рис. 4.12.

Решение. Смотри табл.4.2.

Таблица 4.2

	и	маршрут	w	v’
Исходные значения	—	D	0	D
	С	DC	3	С
	А	DCA	9	А
	В	DCAB	14	В
Последний проход	В	DCABD	24	В

В результате работы алгоритма был найден гамильтонов цикл DCABD общего веса 24. Делая полный перебор всех циклов в этом маленьком графе, можно обнаружить еще два других гамильтоновых цикла: ABCDA общего веса 23 и ACBDA общего веса 31. В полном графе с двадцатью вершинами существует приблизительно 6.1*10¹⁶ гамильтоновых циклов, перечисление которых требует чрезвычайно много машинной памяти и времени.

4.3. Деревья

Есть класс графов, называемых деревьями, которые особенно интенсивно используются в вычислительных приложениях. Граф G = (V, Е) называется деревом, если он связен и ацикличен (т.е. не содержит циклов).

Граф называется связным, если для любых его двух вершин существует маршрут, соединяющий эти вершины. Связный подграф, не являющийся собственным подграфом никакого другого подграфа исходного графа, называется компонентой связности графа.

Деревья являются в некотором смысле простейшим классом графов. Для них выполняются многие свойства, которые не выполняются для графов в общем случае. Деревья являются своего рода носителями связности.

Неориентированное дерево – это связный неориентированный граф без циклов, а следовательно, без петель и кратных ребер. Несвязный (неориентированный) граф без циклов называется лесом. Связные компоненты леса являются деревьями. Любая часть дерева или леса также не имеет циклов, т. е. является деревом или лесом. В качестве примера рассмотрим диаграммы всевозможных деревьев с четырьмя вершинами и леса (рис 4.13.).

Дерево с корнем или корневое дерево получается, если в дереве (связном ациклическом неориентированном графе) выделить одну из вершин, назвав ее корнем. Графически корневое дерево можно изобразить так, как это сделано на рис. 4.13. В).

А) Б) В)

Рис. 4.13. А) Деревья; Б) Лес; В) Корневое дерево.

Таким образом, деревом называется связный неорграф, не содержащий циклов. Любой неорграф без циклов называется ациклическим графом или лесом. Таким образом, компонентами связности любого леса являются деревья.

Пусть G = (V, Е) — граф с п вершинами и т ребрами. Можно сформулировать несколько необходимых и достаточных условий, при которых G является деревом:

• Любая пара вершин в G соединена единственным путем.

• G связен и т = п — 1.

• G связен, а удаление хотя бы одного его ребра нарушает связность графа.

• G ацикличен, но если добавить хотя бы одно ребро, то в G появится цикл.

Эквивалентность большинства из этих условий устанавливается без особого труда. Наиболее сложно разобраться со вторым из них. В следующем примере мы докажем, что дерево с п вершинами имеет ровно (п — 1) ребро.

Пример 7. Докажите с помощью индукции по числу вершин, что для дерева Теп вершинами и т ребрами выполнено соотношение: т = п - 1.

Решение. Поскольку дерево с единственной вершиной вообще не содержит ребер, то доказываемое утверждение справедливо при п = 1.

Рассмотрим дерево Т с n вершинами (и т ребрами), где п > 1 и предположим, что любое дерево с k < п вершинами имеет ровно k - 1 ребро.

Удалим ребро из Т. По третьему свойству дерево Т после этой процедуры превратится в несвязный граф. Получится ровно две компоненты связности, ни одна из которых не имеет циклов (в противном случае исходный граф Т тоже содержал бы циклы и не могбы быть деревом). Таким образом, полученные компоненты связности — тоже деревья.

Обозначим новые деревья через T₁ и T₂. Пусть п₁ количество вершин у дерева T₁, а п₂ - у Т₂. Поскольку п₁ + п₂ = n то п₁< п и п₂ < п.

По предположению индукции дерево T₁ имеет n₁ — 1 ребро, а Т₂ — п₂ – 1. Следовательно, исходное дерево Т насчитывало (с учетом одного удаленного) (п₁ - 1) + (п₂ - 1) + 1 = п - 1 ребро, что и требовалось доказать.

Несложно доказать, что в любом связном графе найдется подграф, являющийся деревом. Подграф в G, являющийся деревом и включающий в себя все вершины G, называется остовным деревом. Остовное дерево в графе G строится просто: выбираем произвольное его ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла. Благодаря примеру 7.7, мы знаем, что для построения остовного дерева в графе из п вершин необходимо выбрать ровно п — 1 ребро.

Пример 8. Найдите два разных остовных дерева в графе, изображенном на рис. 4.14.

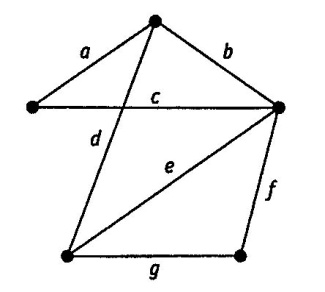
Рис. 4.14. Связный граф G

Решение. В этом графе существует несколько остовных деревьев. Одно из них получается последовательным выбором ребер: a, b, d и f. Другое — Ь, с, е и g. Названные деревья показаны на рис. 4.14. Процесс, описанный в примере 8, можно приспособить для решения задачи поиска кратчайшего соединения: Нужно построить железнодорожную сеть, связывающую некоторое число городов. Известна стоимость строительства отрезка путей между любой парой городов. Требуется найти сеть минимальной стоимости.

Ha языке теории графов нам нужно в нагруженном графе найти остовное дерево наименьшего общего веса. Такое дерево принято называть минимальным остовным деревом или, сокращенно, МОД. В отличие от задачи коммивояжера, здесь есть эффективный алгоритм, находящий действительно минимальное остовное дерево.

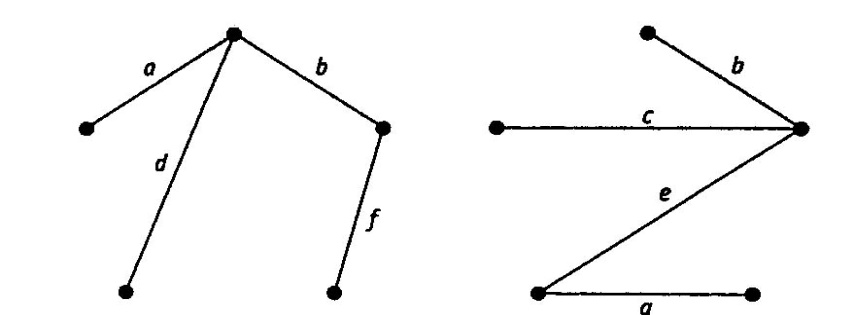
Рис. 4.15. Остовные деревья графа G

Пусть G = (V; E) – неориентированный граф (неорграф). Часть G' = (V';E') графа G является остовом или каркасом графа G, если V = V' и G' — лес, который на любой связной компоненте графа G образует дерево.

Таким образом, если G — связный граф, то остов G' является деревом, которое будем называть остовным деревом графа G. Понятие остова для орграфа G определяется как часть G графа G, для которой F(G') является остовом графа F(G). Аналогично вводится понятие остовного дерева для связного орграфа С.

Очевидно, что в каждом графе существует остов: Разрушая в каждой связной компоненте циклы, т. е. удаляя лишние ребра, получаем остов.

Из вышесказанного вытекает следующее:

1) Число ребер произвольного неорграфа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно т - п + с, где т — число ребер, п — число вершин, с — число компонент связности графа G.

Доказательство. Действительно, если i-я компонента связности С_i графа G содержит n_i вершин, то соответствующее дерево K_i остова содержит n_i - 1 ребро. Следовательно, для получения К_i из компоненты С_i нужно удалить m_i - (n_i - 1) ребер, где т_i — число ребер в C_i. Суммируя удаляемые ребра по всем компонентам связности и замечая, что получаем, что необходимо удалить ребер.

Число v(G) = т-п + с называется цикломатическим числом или циклическим рангом графа G. Число v*(G) = п - с называется коциклическим рангом или корангом. Таким образом, v*(G) есть число ребер, входящих в любой остов rpacpa G, и v(G) + v*(G)=m.

Пример 9. В качестве остова графа G, изображенного на рис. 17, можно взять лес с ребрами 2, 3, 4 и 6, 7 (вообще говоря, остов определяется неоднозначно).

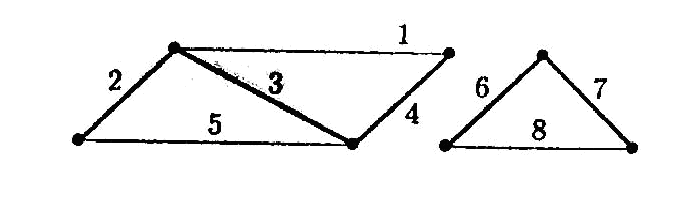
Рис. 4.16.

2) Неорграф G является лесом тогда и только тогда, когда v(G) = 0.

3) Неорграф G имеет единственный цикл тогда и только тогда, когда v(G) = 1.

Решение задачи нахождения остова минимального веса во взвешенном графе G = (V;E), заключается в следующем.

1. Строим граф Т_i, состоящий из множества вершин V и единственного ребра u_i, которое имеет минимальный вес.

2. Если граф T_i, уже построен и i < n – с, где п – количество вершин, с = c(G) – скомпонента связности, то строим граф Т_i+1, добавляя к множеству ребер графа Т_i ребро u_i+1, имеющее минимальный вес среди ребер, не входящих в Т_i и не составляющих циклов с ребрами из T_i.

Приведенный алгоритм, в частности, позволяет находить, остов в невзвешенном графе, положив w(u_i) = 1 для всех ребер u_i Є R.

Пример 10. На рис. 4.17 показан остов минимального веса взвешенного графа. Вес остова равен 9

.

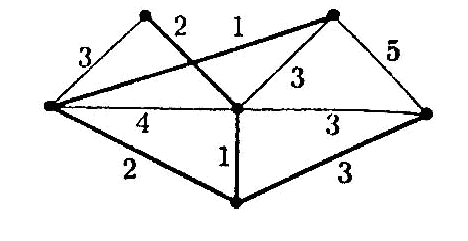
Рис. 4.17.