
- •Глава 4. Графы
- •4.1. Введение в теорию графов
- •Графы и терминология
- •4.2. Гамильтоновы графы
- •Алгоритм ближайшего соседа
- •4.3. Деревья
- •Поиск минимального остовного дерева
- •Контрольные вопросы
- •Задачи для самостоятельного решения
- •Основные тезисы
- •4.4. Ориентированные графы
- •Алгоритм топологической сортировки
- •Пути в орграфах
- •Кратчайший путь
- •Алгоритм Дейкстры
- •Контрольные вопросы.
- •Задания для самостоятельного выполнения
- •Основные тезисы
Глава 4. Графы
4.1. Введение в теорию графов
Настоящая глава посвящена теории графов. Теория графов применяется в таких областях, как физика, химия, теория связи, проектирование ЭВМ, электротехника, машиностроение, архитектура и т. д. Эта теория тесно связана со многими разделами математики, среди которых теория групп, теория матриц, численный анализ, теория вероятностей, топология и комбинаторный анализ. На графах рассматриваются важные практические проблемы, многие из которых требовали тонких математических методов. Уже в середине XIX века Киргхоф применил графы для анализа математических цепей, а Кэли исследовал важный класс графов для выявления и перечисления изомеров насыщенных углеводородов (1857г.). Однако теория графов как математическая дисциплина сформировалась только в середине 30-х годов XX века благодаря работам таких математиков, как Кениг Г., Понтрягин Л.С., Зыков А.А., Визинг В.Г., и другие.
Впервые понятие «граф» ввел в 1936 году венгерский математик Денни Кениг. Но первая работа по теории графов принадлежит Леонарду Эйлеру и была написана еще в в 1736 году. Известный математик Леонард Эйлер, пытался решить теперь уже классическую задачу о Кенигсбергских мостах. В то время в городе Кенигсберге было два острова, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рис. 1.1. Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра — с мостами, которыми связаны эти части. Как мы покажем, Эйлеру удалось доказать, что искомого маршрута обхода города не существует.
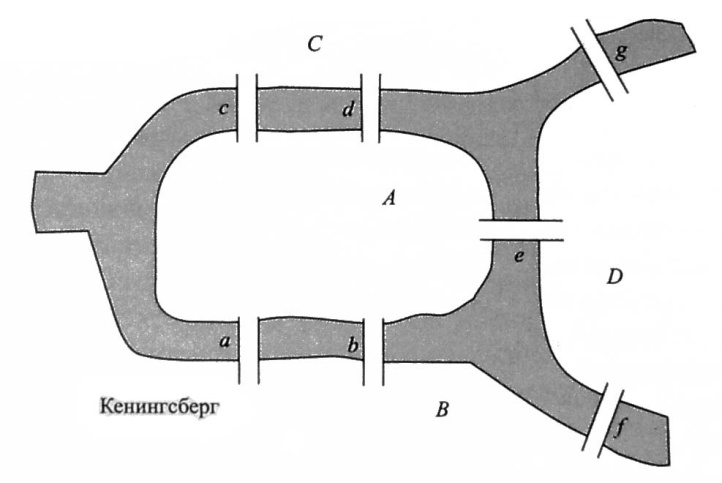
Рис.4. 1. Схема старого Кенигсберга
Графы и терминология
На рис. 4.1 изображены семь мостов Кенигсберга так, как они были расположены в восемнадцатом столетии. В задаче, к которой обратился Эйлер, спрашивается: можно ли найти маршрут прогулки, который проходит ровно один раз по каждому из мостов и начинается и заканчивается в одном и том же месте города?
Модель задачи — это граф, состоящий из множества вершин и множества ребер, соединяющих вершины. Вершины А, В, С и D символизируют берега реки и острова, а ребра а, b, с, d, e, f и g обозначают семь мостов (см. рис. 4.2). Искомый маршрут (если он существует) соответствует обходу ребер графа таким образом, что каждое из них проходится только один раз. Проход ребра, очевидно, соответствует пересечению реки по мосту.
Граф, в котором найдется маршрут, начинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется эйлеровым графом. Последовательность вершин (может быть и с повторениями), через которые проходит искомый маршрут, как и сам маршрут, называется эйлеровым циклом. Эйлер заметил, что если в графе есть эйлеров цикл, то для каждого ребра, ведущего в какую-то вершину, должно найтись другое ребро, выходящее из этой вершины, и получил из этого простого наблюдения такой вывод: если в данном графе существует эйлеров цикл, то к каждой вершине должно подходить четное число ребер.
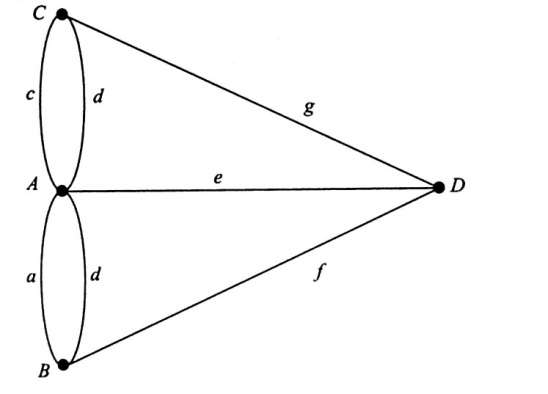
Рис.4.2. Модель задачи о мостах Кенигсберга.
Кроме того, Эйлеру удалось доказать и противоположное утверждение, так что граф, в котором любая пара вершин связана некоторой последовательностью ребер, является Эйлеровым тогда и только тогда, когда все его вершины имеют четную степень. Степенью вершины v называется число S(v) ребер из нее выходящих (ей инцидентных). Вершина степени 1 называется висячей. Вершина степени 0 называется изолированной.
Теперь
совершенно очевидно, что в графе,
моделирующем задачу о мостах Кенигсберга,
эйлерова цикла найти нельзя. Действительно,
степени всех его вершин нечетны:
 (В)
=
(С) —
(D)
= 3 и
(А) = 5. С легкой руки
Эйлера графы, подобные тому, который мы
исследовали при решении задачи о мостах,
стали использоваться при решении многих
практических задач, а их изучение выросло
в значительную область математики.
(В)
=
(С) —
(D)
= 3 и
(А) = 5. С легкой руки
Эйлера графы, подобные тому, который мы
исследовали при решении задачи о мостах,
стали использоваться при решении многих
практических задач, а их изучение выросло
в значительную область математики.
Простой граф определяется как пара G = (V, Е), где V — конечное множество вершин, а Е — конечное множество ребер, причем G не может содержать петель (ребер, начинающихся и заканчивающихся в одной вершине) и кратных ребер (кратными называются несколько ребер, соединяющих одну и ту же пару вершин). Естественно, что множество ребер графа не может быть пустым, в то время как множество ребер (дуг) может быть пустым.
Граф, изображенный на рис. 1, не является простым, поскольку, например, вершины А и В соединяются двумя ребрами (как раз эти ребра и называются кратными).
Графы бывают двух
видов – ориентированные и
неориентированные. Ориентированным
графом (орграфом) называется тройка
G
= (V,
Е,f),
где V
– множество вершин
графа, Е
– множество дуг, а ,f
– отображение
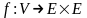 ,
называемое отображением инцидентности.
,
называемое отображением инцидентности.
В
орграфе каждому ребру (дуге)
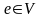 однозначно отвечает упорядоченная
пара точек (вершин)
однозначно отвечает упорядоченная
пара точек (вершин)
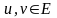 ,
в то время, как в неориентированном
графе порядок перечисления вершин роли
не играет.
,
в то время, как в неориентированном
графе порядок перечисления вершин роли
не играет.
Ребро е соединяет вершины и и v, а вершины при этом называются концевыми. Ребра, имеющие одинаковые концевые вершины и сами одинаково направленные, называются параллельными (кратными); противоположно направленные ребра – противоположными. Вершина и ребро называют инцидентными друг другу, если вершина является для этого ребра концевой точкой. Две вершины и и v в простом графе называются смежными, если они соединяются каким-то ребром е, про которое говорят, что оно инцидентно вершине и (и v).
Таким образом, мы можем представлять себе множество Е ребер как множество пар смежных вершин, определяя тем самым нерефлексивное, симметричное отношение на множестве V. Рефлексивность отношения, в данном случае, обозначает то, что в простом графе нет петель, т. е. ребер, оба конца которых находятся в одной вершине. Симметричность отношения вытекает из того факта, что ребро е, соединяющее вершину и с v, соединяет и v c и (иначе говоря, ребра не ориентированы, т. е. не имеют направления). Единственное ребро простого графа, соединяющее пару вершин и и v, мы будем обозначать как uv (или vu).
Логическая матрица отношения на множестве вершин графа, которое задается его ребрами, называется матрицей смежности. Матрица смежности заполняется символами «И» или «Л» (или «1» или «0») в зависимости от того, соединены или нет вершины в графе. Симметричность отношения в терминах матрицы смежности М означает, что матрица М симметрична относительно главной диагонали. Рефлексивность отношения в терминах матрицы смежности означает наличие на главной диагонали символа «И» (или «1»). А нерефлексивность этого отношения означает наличие на главной диагонали матрицы М стоит символа «Л» (или «0»).
Пример 1. Нарисуйте граф G(V,E) с множеством вершин V={a,b,c,d,e} и множеством ребер E={ab, ae, bc, bd, ce, de}. Выпишите его матрицу смежности.
Решение. Граф G показан на рис.4.3..
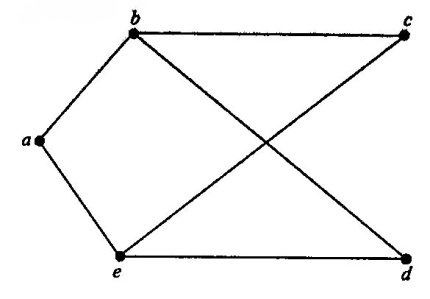
Рис. 4.3.
Его матрица смежности имеет вид:
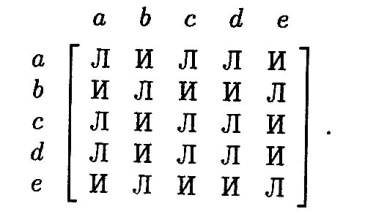
Для восстановления графа нам достаточно только тех элементов матрицы смежности, которые стоят над главной диагональю.
Путем в графе называется такая последовательность ребер, ведущая от некоторой начальной вершины u в некоторую вершину v, в которой каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.
Пример 2. На рис.4.4 произвольный ориентированный граф задан своей диаграммой. Проиллюстрировать на этом графе введенные выше понятия.
 Рис.4.4.
Рис.4.4.
Решение.
Граф G
= (V,
Е,f)
имеет множество вершин
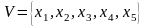 множество дуг
множество дуг
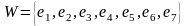 ,
при этом
,
при этом
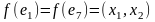 ;
;
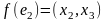 ;
;
 ;
;
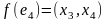 ;
;
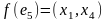 ;
;
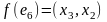 .
.
Ребра
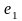 и
и
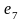 – параллельные ребра;
– параллельные ребра;
ребра
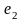 и
и
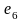 – противоположные ребра;
– противоположные ребра;
ребро
как и ребро
инцидентно вершинам
 и
и
 ;
;
ребро
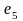 инцидентно вершинам
инцидентно вершинам
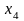 и
и
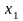 ;
и т. д.
;
и т. д.
Вершины и , и , и , и , и – являются смежными.
Пары
ребер
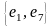 ,
,
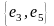 ,
,
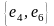 и т.д. так же являются смежными.
и т.д. так же являются смежными.
Степень
вершин
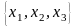 равна 4, степень вершины
равна 2, степень вершины
равна 4, степень вершины
равна 2, степень вершины
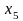 равна 0 – она является изолированной.
равна 0 – она является изолированной.
Последовательность
ребер
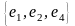 ,
,
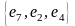 ,
,
 и
и
 образуют пути, ведущие из вершины
в вершину
.
образуют пути, ведущие из вершины
в вершину
.
Путь для неориентированных графов называется маршрутом. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей.
В любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные и отрицательные степени вершин, которые равны числу исходящих из вершины ребер и заходящих в вершину ребер. Суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.
Граф
без петель и кратных ребер называют
простым графом.
Граф без петель, но с кратными ребрами
называют мультиграфом.
Наиболее общий случай графа, когда
допускаются петли и кратные ребра,
называют псевдографом.
Граф без ребер называют нуль-графом.
Простой граф, в котором любые две вершины
соединены ребром, называется полным.
Если множество вершин V
простого графа допускает разбиение на
два непересекающихся подмножества
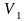 и
и
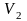 ,
(
,
(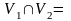 Ø)
так, что не существует ребер, соединяющих
вершины одного и того же подмножества,
то граф называется двудольным или
биграфом (рис. 4.5.)
Ø)
так, что не существует ребер, соединяющих
вершины одного и того же подмножества,
то граф называется двудольным или
биграфом (рис. 4.5.)

Рис. 4.5. Пример двудольного графа
Маршрутом длины k в графе G называется такая последовательность вершин v0,v1,…,vk, что для каждого i= 1,...,k пара vi-1vi образует ребро графа. Мы будем обозначать такой маршрут через v0 v1…vk.
Маршрут, все ребра которого различны, называется цепью. Маршрут, у которого различны все вершины, называется простой цепью. Замкнутая цепь называется циклом, а замкнутая простая цепь – простым циклом.
Или циклом в графе принято называть последовательность вершин v0,v1,…,vk, каждая пара которых является концами одного ребра, причем v0=v1, а остальные вершины (и ребра) не повторяются. Иными словами, цикл — это замкнутый маршрут, проходящий через каждую свою вершину и ребро только один раз.
Граф, в котором нет циклов, называется ацикличным. Структуры деревьев, которые возникают в вычислениях, представляют собой частный случай ацикличных графов.
Пример 3. Пример цепей и циклов в псевдографе приведен на рис.4. 6.
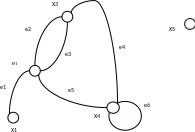 Рис.
4.6.
Рис.
4.6.
Пример
цепей и циклов в псевдографе:
 – цепь;
– цепь;
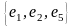 – простая цепь;
– простая цепь;
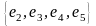 – цикл;
– цикл;
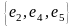 – простой цикл.
– простой цикл.
Для ориентированных графов все введенные понятия сохраняются с заменой терминов маршрутов на путь, а цикла на контур.
Граф
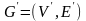 называется частью
графа G
= (V,
Е), если Е'
называется частью
графа G
= (V,
Е), если Е'
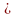 Е и V’
V.
Часть графа, которая наряду с некоторым
подмножеством ребер содержит и все
инцидентные им вершины, называется
подграфом. Часть графа, которая наряду
с некоторым подмножеством ребер содержит
все вершины графа (Е'
Е и V’
= V),
называется суграфом. Примеры разных
частей графа приведены на рис. 4.7.
Е и V’
V.
Часть графа, которая наряду с некоторым
подмножеством ребер содержит и все
инцидентные им вершины, называется
подграфом. Часть графа, которая наряду
с некоторым подмножеством ребер содержит
все вершины графа (Е'
Е и V’
= V),
называется суграфом. Примеры разных
частей графа приведены на рис. 4.7.
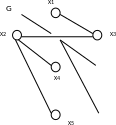
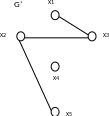
а) б)
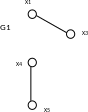
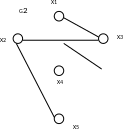
в) г)
Рис. 4.7. Примеры различных частей графа G: а) неориентированный граф G; б) G’ – часть графа G; в) G1 – подграф G; г) G2 – суграф G.
Граф называют связным, если любую пару его вершин соединяет какой-нибудь маршрут. Любой общий граф можно разбить на подграфы, каждый из которых окажется связным. Минимальное число таких связных компонент называется числом связности графа и обозначается через c(G). Вопросы связности имеют важное значение в приложениях теории графов к компьютерным сетям. Следующий алгоритм применяется для определения числа связности графа.
Пример 4. Проследите за связностью на графе, изображенном на рис. 4.8.
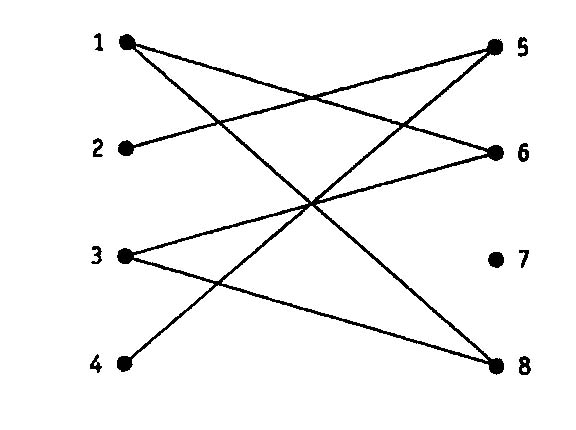 Рис4.8.
Рис4.8.
Решение. Смотри табл. 4.1.
Таблица 4.1.
|
V’ с |
Исходные значения Выбор у = 1 Выбор у = 2 Выбор у = 7 |
{1, 2, 3, 4, 5, 6, 7, 8} 1 {1,3,6,8} 2 {2, 4, 5} 3 {7} |
Итак, c(G) = 3. Соответствующие компоненты связности приведены на рис. 4.9.
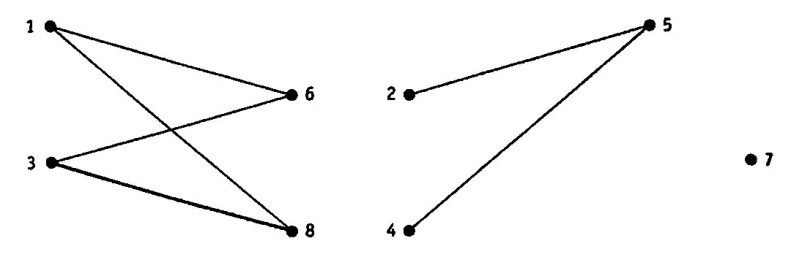
Рис. 4.9.
