Государственное образовательное учреждение

высшего профессионального образования

«Казанский государственный технологический университет»

Нижнекамский химико-технологический институт

В.В.Гетман, Н.В.Лежнева

АНАЛИЗ И СИНТЕЗ ЛИНЕЙНЫХ СИСТЕМ

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Лабораторный практикум

Казань

КГТУ

2007

УДК –

ББК –

Гетман, В.В.

Анализ и синтез линейных систем автоматического управления: лабораторный практикум / В.В.Гетман, Н.В. Лежнева. – Казань: Изд-во Казан. гос. технол. Ун-та, 2007. – 64с.

Приведены лабораторные работы по разделам дисциплины «Теория автоматического управления». Рассмотрены статические и динамические характеристики линейных систем, устойчивость линейных систем, синтез систем автоматического управления.

Предназначен для студентов, обучающихся по направлениям «Информатика и вычислительная техника», «Автоматизированные технологии и производства».

Подготовлен на кафедре «Автоматизация технологических процессов и производств» Нижнекамского химико-технологического института КГТУ.

Печатается по решению редакционно-издательского совета Казанского государственного технологического университета.

Рецензенты: канд. физ.-мат. наук, доц. Н.Н.Саримов

канд. физ.-мат. наук доц. О.В.Шемелова

Содержание

Введение………………………………………………........4

Лабораторная работа №1. Временные и частотные характеристики линейных систем автоматического управления……..6

Лабораторная работа №2. Исследование динамических

характеристик типовых динамических звеньев...........................18

Лабораторная работа №3. Исследование линейных систем регулирования………………………………………..….........33

Лабораторная работа №4. Анализ и синтез САУ методом

корневого годографа……………………………...........................45

Лабораторная работа №5. Определение настроек регуля­тора методом незатухающих колебаний………….......................56

Библиографический список................................................64

Введение

управления, начиная с изучения динамических характеристик При автоматизации технологических объектов управления широко применяют одноконтурные САУ, обеспечивающие стабилизацию выходных координат объектов. Синтез таких систем предполагает знание статических и динамических характеристик ТОУ, позволяющих определить структуру регулятора и найти параметры его настройки.

Первый шаг процесса синтеза – определить назначенияесистемы. Второй шаг – это указать те переменные, которые подлежат управлению (например, температура, давление, уровень, концентрация и т.д.). На третьем шаге необходимо предъявить требования к точности. Следующий шаг – это выбор конфигурации системы, которая обладала бы желаемым качеством. Такая конфигурация обычно включает в себя датчик, объект управления, исполнительное устройство и регулятор.

Затем необходимо составить математическое описание объекта управления. Для этого требуется установить все взаимосвязи между переменными, характеризующими поведение объекта. В качестве описания можно использовать дифференциальные уравнения. Если эти уравнения могут быть линеаризованы, то можно воспользоваться преобразованием Лапласа. В результате мы можем получить передаточную функцию объекта управления.

Далее необходимо выбрать регулятор. Выбор типа регулятора может начинаться с простейших двухпозиционных регуляторов и заканчиваться самонастраивающимся микропроцессорным регулятором.

Заключительный шаг процедуры синтеза состоит в настройке параметров системы, которые обеспечивали бы желаемые показатели качества.

Данный лабораторный практикум посвящен преимущественно изучению основных этапов синтеза систем автоматического объекта управления и заканчивая получением оптимальных настроечных параметров регулятора и оценкой качества переходных процессов в САУ.

Лабораторная работа №1.

ВРЕМЕННЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Цель работы: Ознакомление с динамическими и частотными характеристиками систем автоматического управления (САУ) и получение навыков исследования линейных систем.

Постановка задачи: В качестве объекта исследования выступают линейные динамические системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов

.

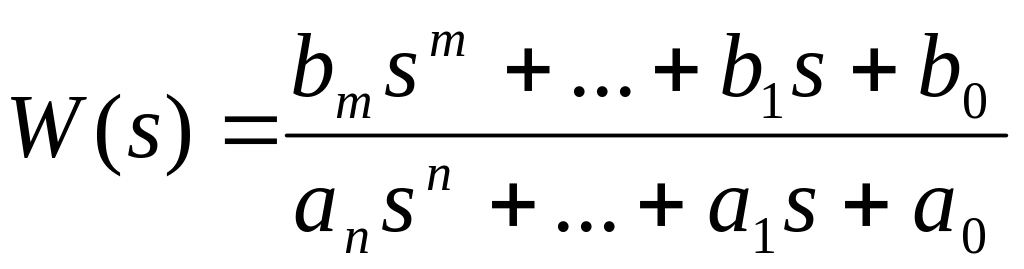Необходимо:

1. Определить полюсы и нули передаточной функции.

2. Записать дифференциальное уравнение, определяющее функционирование САУ.

3. Построить графики переходной и импульсной переходной функции: h(t), w(t).

4. Построить логарифмические частотные характеристики L(ω).

5. Построить частотный годограф Найквиста W(iω).

Теоретические сведения

В качестве объекта исследования предлагается разомкнутая система, представленная на рис. 1.1.

Рис. 1.1. Структурная схема разомкнутой системы: u – входной сигнал; y – выходной сигнал

Уравнение линейной стационарной системы с одним входом и одним выходом можно записать в следующем виде:

.

После преобразования по Лапласу мы получим это же уравнение в операторной форме:

.

Передаточная функция представляет собой отношение преобразованного по Лапласу выхода системы y(p) к преобразованному по Лапласу входу u(p):

.

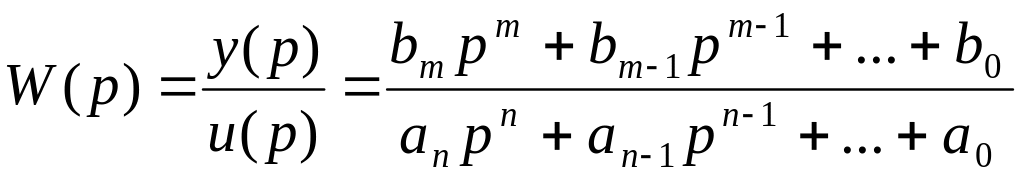Функцию W(iω), которую получаем из передаточной функции при подстановке , называют амплитудно-фазовой характеристикой (АФХ):

.

Функцию W(iω) можно представить в виде:

,

где U(ω) – вещественная частотная характеристика;

V(ω) – мнимая частотная характеристика;

- амплитудная частотная характеристика (АЧХ);

- фазовая частотная характеристика (ФЧХ).

Для исследования частотных свойств системы удобно использовать графические изображения частотных характеристик. В этом случае амплитудно-фазовая характеристика W(iω) строится в плоскости комплексного переменного и представляет собой годограф вектора, длина (модуль) которого равна A(ω), а аргумент (угол, образованный этим вектором с действительной, положительной полуосью) – φ(ω):

;

.

Наряду с рассмотренными частотными характеристиками в теории автоматического управления используются логарифмические частотные характеристики. Удобство работы с ними объясняется тем, что операции умножения и деления заменяются на операции сложения и вычитания, а это позволяет во многих случаях строить их практически без вычислений.

Амплитудная частотная характеристика, построенная в логарифмическом масштабе,

,

называется логарифмической амплитудной частотной характеристикой (ЛАЧХ). При этом амплитуда измеряется в децибелах (дБ).

Другой важной характеристикой автоматических систем (звеньев) являются переходные и импульсные переходные функции и их графики – временные характеристики. Их используют при описании линейных систем - как стационарных, так и нестационарных.

Переходной функцией системы называют функцию, описывающую изменение выходной величины системы, когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях. Переходную функцию (рис. 1.2) обычно обозначают h(t).

О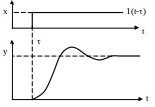 тметим, что единичная ступенчатая функция - это функция, которая обладает свойством

График переходной функции – кривую зависимости h(t) от t на-

Рис. 1.2. Пример переходной характе- зывают кривой разгона.

ристики системы

И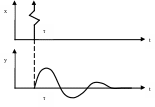 мпульсная переходная функция (характеристика) g(t) пред­ставляет собой реакцию на входное воздействие типа единичной импульсной функции при нулевых начальных условиях (рис. 1.3).

Такое входное

Рис. 1.3. Пример импульсной переход- воздействие математи-

ной характеристики системы чески отражает дельта-

функция, которая обладает следующими свойствами:

1. ;

2.

Для выполнения лабораторной работы используется пакет прикладных программ (ППП) Control System Toolbox. ППП предназначен для работы с LTI-моделями (Linear Time Invariant Models) систем управления.

В Control System Toolbox имеется тип данных, определяющих динамическую систему в виде комплексной передаточной функции. Синтаксис команды, создающий LTI-систему c одним входом и одним выходом в виде передаточной функции:

TF([b_m, …, b₁, b₀], [a_n, …, a₁, a₀]),

где b_m, …, b₁ – значения коэффициентов полинома, стоящего в числителе передаточной функции.

a_n, …, a₁ – значения коэффициентов полинома A, стоящего в знаменателе..

Для выполнения работы могут применяться команды, приведенные в таб. 1.1.

Другим вариантом получения графиков динамических характеристик САУ является использование графического интерфейса ППП CST – LTI viewer, вызов которого осуществляется командой ltiview, которой, в качестве параметра, можно указать имя переменной, содержащей LTI-объект.

Таблица 1.1. Некоторые команды Control System Toolbox

Команда	Описание функций
pole	Вычисление полюсов передаточной функции

Окончание табл.1.1

Команда	Описание функций
zero	Вычисление нулей передаточной функции
step	Построение графика переходного процесса
impulse	Построение графика импульсной переходной функции
bode	Построение логарифмических частотных характеристик (диаграммы Боде)
nyquist	Построение частотного годографа Найквиста

Последовательность выполнения работы

Лабораторная работа выполняется поэтапно:

1. изучить теоретические сведения;

2. запустить систему MATLAB;

3. создать tf-объект, в соответствии с заданным вариантом.

4. составить дифференциальное уравнение, определяющее функционирование САУ;

5. определить полюса передаточной функции с использованием команды pole;

6. определить нули передаточной функции с использованием команды zero;

7. используя LTI-viewer, или соответствующие команды (табл.1.1) получить динамические характеристики – переходную функцию h(t), импульсно-переходную функцию w(t) и частотные характеристики – диаграмму Боде, частотный годограф Найквиста;

8. получить представление исходной функции в виде произведения типовых звеньев;

9. ответить на контрольные вопросы;

10. оформить отчет;

11. сдать отчет преподавателю и защитить работу;

Методический пример

Задана передаточная функция САУ

Найдем ее динамические и частотные характеристики. Будем работать в командном режиме среды MATLAB.

1. Создадим LTI-объект с именем w:

>> w = tf([1,2],[3,4,5,3])

Transfer function:

s + 2

-----------------------

3 s^3 + 4 s^2 + 5 s + 3

2. Найдем полюса и нули передаточной функции с использованием команд pole, zero.

>> pole(w)

ans =

-0.2639 + 1.0825i

-0.2639 - 1.0825i

-0.8055

>> zero(w)

ans =

-2

3. Построим график переходной функции командой step(w) (рис. 1.4):

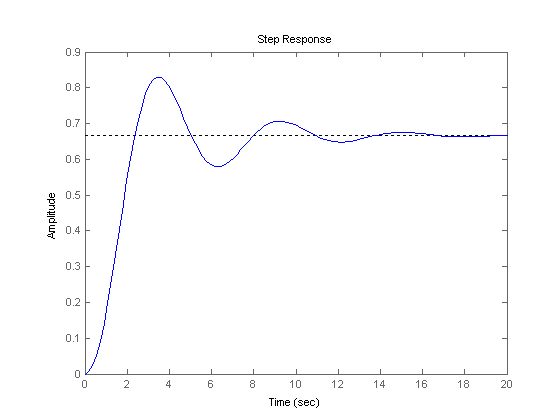
Рис. 1.4. График переходной характеристики

4. Построим импульсную переходную функцию командой impulse(w):

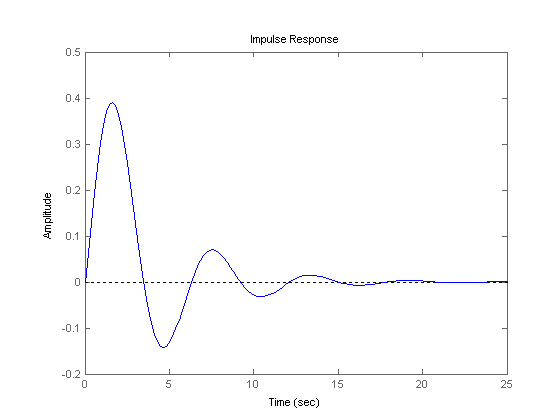
Рис. 1.5. График импульсной переходной функции

5. Графики ЛАЧХ и ЛФЧХ, а также АФХ получим, используя команды bode(w) (рис. 1.6а) и nyquist(w) (рис. 1.6б):

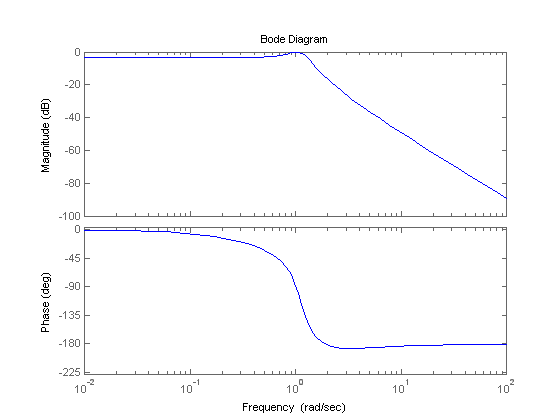
а)

б)

Рис. 1.6. Графики ЛАЧХ, ЛФЧХ и АФХ

Аналогичные результаты можно получить, используя команду ltiview(w), с соответствующими настройками в меню “Plot Configuration”.

Варианты заданий

Вид передаточной функции:

1. ;

2. ;

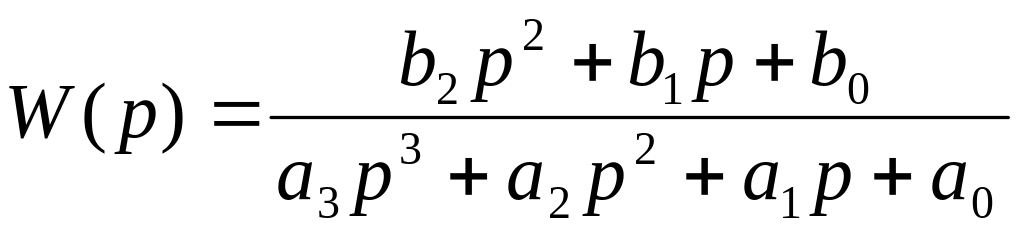3. ;

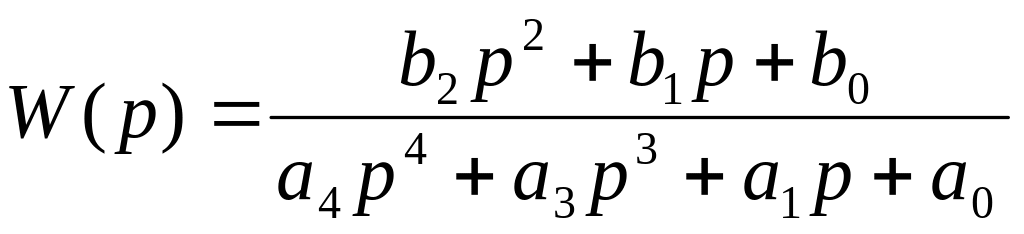Вид передаточной функции	№ варианта	Коэффициенты полиномов
		b0	b1	a0	a1	a2	a3	а4
1	1.	0	3	1	2	3	0	1
	2.	2	6	4	0	1	5	1
	3.	0	-3	5	2	0	2	1
	4.	4	2	3	4	5	3	1
	5.	0	1	-2	-2	-3	-2	0
		b0	b1	b2	a0	a1	a2	а3
2	1.	0	-3	2	4	2	3	9
	2.	8	0	-3	-4	-6	-4	-1

Окончание таблицы

Вид передаточной функции	№ варианта	Коэффициенты полиномов
	3.	-4	6	-2	5	5	0	1
	4.	6	-8	-7	0	-6	-3	-1
	5.	2	-1	-3	-1	0	-7	-2
		b0	b1	b2	a0	a1	a3	a4
3	1.	0	2	8	-3	7	-7	1
	2.	-5	0	3	-8	-2	-1	-6
	3.	-7	1	2	0	5	2	9
	4.	-6	4	-4	1	0	6	3
	5.	2	-2	-1	5	3	0	9

 

Контрольные вопросы

1. Что называется нулями и полюсами передаточной функции?

2. Что называется переходной характеристикой?

3. Что называется импульсной переходной характеристикой?

4. Что называется частотными характеристиками?

5. Как определяется АЧХ?

6. Как определяется ФЧХ?

7. Как строится годограф АФХ?

8. Как получают кривую разгона?

9. Какая связь между передаточной функцией и временными характеристиками?