- •Случайные события. Вероятность. Теоремы сложения и умножения.
- •Случайные величины. Законы распределения дискретных и непрерывных случайных величин
- •Числовые характеристики дискретных и непрерывных случайных величин
- •Системы случайных величин. Законы распределения и числовые характеристики
- •Генеральная и выборочная совокупность. Выборочные характеристики
- •21. Нелинейная парная регрессия. 2 типа нелинейных регрессий.
- •23. Индексы корреляции и детерминации в нелинейных регрессиях.
- •24. Классическая нормальная линейная модель множественной регрессии.
- •28. Коэффициенты множественной детерминации и корреляции
- •29. Оценка значимости уравнения в целом и его параметров в отдельности
- •30. Доверительный интервал для коэффициентов множественной регрессии
- •31. Доверительные интервалы для индивидуальных прогнозных значений зависимой переменной
- •32. Частные f-критерии и их использование в эконометрике
- •33. Мультиколлинеарность, ее разновидности, последствия и способы выявления
- •37. Устранение гетероскедастичности. Взвешенный метод наименьшего квадрата.
- •38. Обобщенная модель множественной регрессии.
- •39. Автокорреляция, ее виды и последствия.
- •40. Методы обнаружения автокорреляции.
- •41.Оценка параметров при наличии автокорреляции.
- •47. Общие понятия временного ряда. Его составляющие. Типы моделей
- •48. Стационарные временные ряды. Коэффициент автокорреляции. Коррелограмма
- •49. Аналитическое и механическое выравнивание временного ряда
- •50. Применение фиктивных переменных при моделировании сезонных колебаний ряда
- •51. Тесты Чоу и Гуйарата для обнаружения структурных изменений ряда
- •Вопрос 52
- •Вопрос 53
30. Доверительный интервал для коэффициентов множественной регрессии
Для построения доверительного интервала для коэффициентов множественной регрессии сначала находят стандартные ошибки параметров по формуле:
Здесь: 1) диагональный элемент обратной матрицы, стоящей на пересечении строки и ( столбца.
2) стандартная ошибка уравнения регрессии.
По таблицам распределения Стьюдента находится , при этом , .
Если , то статистически значим, т.е. существенно отличается от 0.
Если , то статистически незначим и фактор можно исключить из модели, т.к. он несущественно влияет на переменную у.
Теперь
можно построить интервальные оценки
для коэффициентов


Замечание!
Если параметр
на
предыдущем этапе признан статистически
незначимым, то интервальная оценка для
не строится, т.к. в этом случае построенный
интервал будет иметь вид:
 ,
,
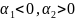 ,
т.е.
,
т.е.
 ,
с вероятностью 0,95
,
с вероятностью 0,95
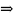 построение лишнее.
построение лишнее.
31. Доверительные интервалы для индивидуальных прогнозных значений зависимой переменной
После того, как найдены стандартные ошибки параметров можно построить интервальные оценки для коэффициентов модельного уравнения регрессии по след. формуле:
Замечание! Если параметр на предыдущем этапе признан статистически незначимым, то интервальная оценка для не строится, т.к. в этом случае построенный интервал будет иметь вид: , , т.е. , с вероятностью 0,95 построение лишнее.
Зафиксируем
значение объясняющих переменных:
 и введем в рассмотрение вектор-столбец
и введем в рассмотрение вектор-столбец
 .
По уравнению регрессии получим прогнозное
значение:
.
По уравнению регрессии получим прогнозное
значение:
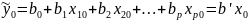

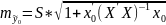
32. Частные f-критерии и их использование в эконометрике
Не
каждый фактор, дополнительно включенный
в модель, может существенно увеличить
долю объясняемой вариации зависимой
переменной. Ввиду корреляции м/у
факторами, значимость влияния одного
и того же фактора м.б. различной в
зависимости от последовательности
включения его в модель. Мерой оценки
значимости улучшения качества модели,
после включения в нее дополнительного
фактора
 ,
служит частный
,
служит частный
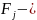 критерий, который опред-ся по след.
формуле:
критерий, который опред-ся по след.
формуле:

Здесь:
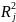 -
коэффициент множ-ой детерминации без
фактора
в
модели.
– коэффициент
множ-ой детерминации с фактором
.
По
таблицам Распределения Фишера наход-ся
по
уровню значимости
и числом степеней свободы
.
-
коэффициент множ-ой детерминации без
фактора
в
модели.
– коэффициент
множ-ой детерминации с фактором
.
По
таблицам Распределения Фишера наход-ся
по
уровню значимости
и числом степеней свободы
.
Если
 ,
то включение в модель
явл-ся оправданным, т.к. он существенно
улучшает качество модели. В противном
случае это включение нецелесообразно.
,
то включение в модель
явл-ся оправданным, т.к. он существенно
улучшает качество модели. В противном
случае это включение нецелесообразно.
Если р = 2, то исп-ся 2 частных F-критерия:
 (1)
(1)
По
таблице распределения Фишера находим
по
и

Если
 ,
то включение фактора
,
то включение фактора
 в модель после того, как в нее был включен
фактор
в модель после того, как в нее был включен
фактор
 является целесообразным. Поскольку
фактор
существенно улучшает качество модели.
В противном случае, т.е. если
является целесообразным. Поскольку
фактор
существенно улучшает качество модели.
В противном случае, т.е. если
 ,
то включение
в модель после того, как в нее был включен
фактор
нецелесообразно. Параметр
,
то включение
в модель после того, как в нее был включен
фактор
нецелесообразно. Параметр
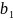 при
не будет статистически значимым.
при
не будет статистически значимым.
Пусть
по п
наблюдениям построено уравнение
регрессии с р
факторами. При этом, коэффициент
детерминации =
.
Исключим из рассмотрения k
объясняющих переменных, которые
показались нам лишними. Получим новую
модель
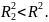 Проверяем
Проверяем
 .
Для проверки гипотезы исп-ся след.
F-критерий:
.
Для проверки гипотезы исп-ся след.
F-критерий:
 .
По таблице Фишера:
по
и
.
По таблице Фишера:
по
и
 .
.
Если
,
то
 отвергается, т.е. коэф множ-ой детерминации
существенно различно и исключение
факторов из модели недопустимо. Аналогично
можно проверить обоснованность
дополнительного включения в модель
факторов. В этом случае исп-ют F-статистику:
отвергается, т.е. коэф множ-ой детерминации
существенно различно и исключение
факторов из модели недопустимо. Аналогично
можно проверить обоснованность
дополнительного включения в модель
факторов. В этом случае исп-ют F-статистику: