- •Случайные события. Вероятность. Теоремы сложения и умножения.
- •Случайные величины. Законы распределения дискретных и непрерывных случайных величин
- •Числовые характеристики дискретных и непрерывных случайных величин
- •Системы случайных величин. Законы распределения и числовые характеристики
- •Генеральная и выборочная совокупность. Выборочные характеристики
- •21. Нелинейная парная регрессия. 2 типа нелинейных регрессий.
- •23. Индексы корреляции и детерминации в нелинейных регрессиях.
- •24. Классическая нормальная линейная модель множественной регрессии.
- •28. Коэффициенты множественной детерминации и корреляции
- •29. Оценка значимости уравнения в целом и его параметров в отдельности
- •30. Доверительный интервал для коэффициентов множественной регрессии
- •31. Доверительные интервалы для индивидуальных прогнозных значений зависимой переменной
- •32. Частные f-критерии и их использование в эконометрике
- •33. Мультиколлинеарность, ее разновидности, последствия и способы выявления
- •37. Устранение гетероскедастичности. Взвешенный метод наименьшего квадрата.
- •38. Обобщенная модель множественной регрессии.
- •39. Автокорреляция, ее виды и последствия.
- •40. Методы обнаружения автокорреляции.
- •41.Оценка параметров при наличии автокорреляции.
- •47. Общие понятия временного ряда. Его составляющие. Типы моделей
- •48. Стационарные временные ряды. Коэффициент автокорреляции. Коррелограмма
- •49. Аналитическое и механическое выравнивание временного ряда
- •50. Применение фиктивных переменных при моделировании сезонных колебаний ряда
- •51. Тесты Чоу и Гуйарата для обнаружения структурных изменений ряда
- •Вопрос 52
- •Вопрос 53
24. Классическая нормальная линейная модель множественной регрессии.
уi=β0+β1*x1+β2*x2i+…+βp*xpi+ε, i=1,n (c черточкой наверху) (1)
yi-значение зависимой переменной у в i-м наблюдении. хji-значение фактора хi в i-м наблюдении. j=1,p(с черточкой); i=1,n(с черточкой). β0-постоянное слагаемое, формально равное значению зависимой переменной у, когда все факторы=0. βi-коэф «чистой» регрессии при i-м факторе, характеризующую связь фактора хi переменной у при неизменности других факторов. На основе многомерной выборки требуется получить оценку уравнения (1) и этой оценкой явл-ся выборочное уравнение множественной регрессии. y~=b0+b1x1+b2x2+…+bpxp. (2). Параметр bj, j-0,p (с черточкой)-это точечная оценка неизвестных коэф βj. Введем в рассмотрение след-е векторы и матрицы.
Y= X=
X=
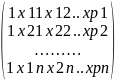 β=
β= b=
b= ε=
ε=
Когда модельное уравнение регрессии =1, то матрица Y запишется: Y=Xp+ε (3)
Введем понятие остатка: еi=yi-y~
e= x=
x=
Тогда выборочное уравнение (2) можно записать в матричной форме: y~=b1*x, «1»- это транспонирование. Из уравнения (2) не трудно получить следующее уравнение, кот называют эмпирическим. yi=b0+b1x1i+b2x2i+…+bpxpi+ei, которое в матричной форме запишется: Y=Xb+e, следовательно, e=Y-Xb.
Чтобы получить оценки коэф модели методом наименьших квадратов, вновь потребуем выполнение для уравнения (1) некоторых условий, которые называются предпосылками МНК:
10.ε-случаный вектор, xi-не явл-ся случайным вектором (СВ).
20.М(εi)=0, i=1,n(с черточкой).
30.D(εi)=δ2=const+ i.
i.
40.M(εi*εj)=0,
i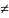 j.
j.
3
и 4 предпосылки: Σε=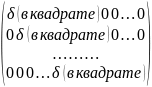 =δ2*Еn.
=δ2*Еn.
50.εi~N(0; δ2)
60.в матрице Х столбцы должны быть неизвестными rank X=p+1.
Если модель (10) удовлетворяет указанным предпосылкам, то она называется классической, нормально, линейной моделью множественной регрессии.
25. МНК-оценки параметров линейной модели множественной регрессии.
уi=β0+β1*x1+β2*x2i+…+βp*xpi+ε, i=1,n (c черточкой наверху) (1)
yi-значение зависимой переменной у в i-м наблюдении. хji-значение фактора хi в i-м наблюдении. j=1,p(с черточкой); i=1,n(с черточкой). β0-постоянное слагаемое, формально равное значению зависимой переменной у, когда все факторы=0. βi-коэф «чистой» регрессии при i-м факторе, характеризующую связь фактора хi переменной у при неизменности других факторов. На основе многомерной выборки требуется получить оценку уравнения (1) и этой оценкой явл-ся выборочное уравнение множественной регрессии. y~=b0+b1x1+b2x2+…+bpxp. (2). Параметр bj, j-0,p (с черточкой)-это точечная оценка неизвестных коэф βj. Введем в рассмотрение след-е векторы и матрицы.
Y= X= β= b= ε=
Когда модельное уравнение регрессии =1, то матрица Y запишется: Y=Xp+ε (3)
Введем понятие остатка: еi=yi-y~
e= x=
Тогда выборочное уравнение (2) можно записать в матричной форме: y~=b1*x, «1»- это транспонирование. Из уравнения (2) не трудно получить следующее уравнение, кот называют эмпирическим. yi=b0+b1x1i+b2x2i+…+bpxpi+ei, которое в матричной форме запишется: Y=Xb+e, следовательно, e=Y-Xb.
Чтобы получить оценки коэф модели методом наименьших квадратов, вновь потребуем выполнение для уравнения уi=β0+β1*x1+β2*x2i+…+βp*xpi+ε, i=1,n (c черточкой наверху) (1)
некоторых условий, которые называются предпосылками МНК:
10.ε-случаный вектор, xi-не явл-ся случайным вектором (СВ).
20.М(εi)=0, i=1,n(с черточкой).
30.D(εi)=δ2=const+ i.
40.M(εi*εj)=0, i j.
3 и 4 предпосылки: Σε= =δ2*Еn.
50.εi~N(0; δ2)
60.в матрице Х столбцы должны быть неизвестными rank X=p+1.
Если модель (10) удовлетворяет указанным предпосылкам, то она называется классической, нормально, линейной моделью множественной регрессии.
Предпосылки
выполняются: Оценки bj, j=0,p(с черточкой)
будем находить методом наименьших
квадратов из условия минимальной
остаточной суммы, т.е.
Qe=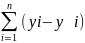 2=
2=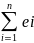 2=e`*e=(Y-Xb)`*(Y-Xb)→min.
2=e`*e=(Y-Xb)`*(Y-Xb)→min.
(d*Qe)/db=-2X`Y+2X`Xb=0.
Отсюда получим нормально уравнение в матричной форме: X`Xb=X`Y.
Если предпосылка (60) выполняется, то (X`X)-1 существует умножая на нее слева, получаем окончательную формулу: b= (X-1X)-1*X`Y (4)
Оценка (4) называется векторной МНК-оценкой и для нее так же справедлива теорема Гаусса Маркова: при выполнении предпосылки 10-60 оценки (4) явл-ся эффективными и несмещенными.
26.уравнение регрессии в стандартизованном масштабе
После этапа параметризации полученное уравнение множественной регрессии в натуральном масштабе
y͂≈b0+b1x1+b2x2+….+bpxp (1)
если факторы х1, х2, …,хр имеют одинаковую размерность (в метрах), то можно соизмерить влияние этих факторов на примере y по значениям абсолютных значениям коэффициентов регрессии |bj|, j=1, p
чем больше модуль, тем сильнее влияет фактор на переменную у
однако, в общем случае, объясняющие переменные xjимеет разную размерность,
поэтому такое сопоставление уже будет недопустимым и некорректным
если возникает необходимость в ранжировании факторов по силе воздействия на переменную у, то прибегают к нормированию коэф-в регрессии, то есть определению стандартизированных коэффициентов регрессии по формуле:
aj=bj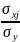 j=1,p (2)
j=1,p (2)
стандартизир-й коэф-т регрессии ajпоказывает на сколько в среднем в своих σу изменяется преимущественно у, если фактор хi больше на одно свое среднее-квадрат-е отклонение при неизменности своих остальных факторов
зная aj уравнение множ-й регрессии можно записать в стандарт масштабе
ty= a1tx1+ a2tx2+…+ aptxp(3)
гдеty=
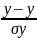 tytx
–стандарт переменные
tytx
–стандарт переменные
txj=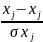 j=1, p
j=1, p
мат ожидание которое равно 0, а среднеквадрат отклонение -1
сравнивая стандарт коэф-ты |aj| можно ранжировать факторы xjпо силе воздействия на переменные у, если даже они имеют разные единицы измерения
зная ajможно найти коэффициент регрессии по слде формуле:
bj
=aj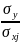 j=1,p
j=1,p
b0=y̅- b1x1̅-b2x2̅-…-bpxp̅
факторы xj можно ранжировать посредним коэффициентом эластичности
Эj̅=bj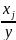 j=
1, p
j=
1, p
27. честные коэффициенты корреляции
Ранжирование факторов по (….) воздействия на переменную у так же можно выполнить с помощью частных коэффициентов корреляции
Они характеризуют тесноту линейной связи междуу и фактором xi при устранении других факторов
Если в модели участвуют з факторов, то различают частные коэф-ты корреляции 1-0, 2-0, …, (р-1)-го порядка