5. Генеральная и выборочная совокупность. Выборочные характеристики

Генеральной совокупностью назыв-ся множество всех возможных значений или реализаций исследуемой СВ Х

Выборочной совокупностью (выборкой) называют часть генеральной совокупности, отобранной для изучения СВ Х.

Кол-во отобранных значений СВ т.е. n наз-ют объемом выборки.

Относительно СВ Х по данной выборке можно определить ряд числовых характеристик, которые в силу этого носят назв. выборочной:

• Выборочные средние = = 1/n

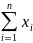
• Выборочная дисперсия Dв = 1/n

• Выборочная ковариация δ_В =

• Выборочный коэффициент корреляции

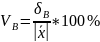
Если исслед-ся 2 СВ (Х,У), то испол-ют след. выборочные харак-ки:

• Выборочная ковариация

• Выборочный коэф. парной корреляции:

Рассмотрим некотор. распределения СВ, используемых в мат статистике.

Нормальное распределение или распределение Гаусса

НСВ имеет нормальное распред-ие с параметрами m,δ, если ее плотность распределения задается след функцией:

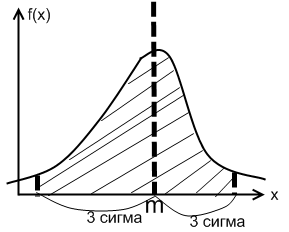
Правило 3-х сигм

(СВ Х имеет нормальное распределение)

Особый интерес представляет частный случай, когда m = 0,δ = 1

X ~ N(0,1) - стандартное нормальное распределение.

Чтобы подсчитать нормальное распределение:

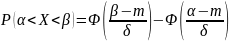
Ф(t) = (1 / dt - функция Лапласа (не берущийся интеграл – поэтому затабулирована)

χ²-распределение

Распределение χ² с k степенями свободы наз-ся распределение квадратов k независимых СВ, распределенных по стандартному нормальному закону, т.е.

χ²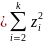 где ~ N(0,1) - независимы

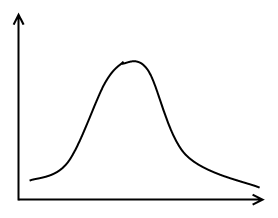
f(χ²)

χ²

При

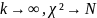
Распределение Стьюдента (t-распределение)

Распределением Стьюдента с степенями свободы наз-ся распределение СВ-ны Т:

, где , - независимые СВ

Распределение Фишера (F - распределение)

Распределением Фишера назыв-ся распре СВ F:

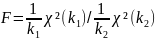, где 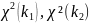– -распределения с и 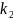степенями свободы. Распределение Фишера харак-ся 2-мя степенями свободы.

№11.Эконометрика дает колич–ое выражение взаимосвязи м/у эконом показателями.

Изучение зависимости эконом–их перем–ых начнем со случая 2–х переем–ых.

Будем обозначать их символами X и Y.

X наз–ся независимой переменной или объясняющая переменная.

Y наз–ся зависимой переменной, объясняемой переменной, результ–м признаком.

Предположим, что для изучения взаимосвязи перем–х X и Y получена двумерная выборка, результат которой приведен в таблице:

Y	Y1	Y2	…	Yn
X	X1	X2	…	Xn

Пример: Xi– колич–во удобрений внесенных на 1 га на i поле.

Yi– кол–во пшеницы собранной с 1 га на i поле.

n–кол–во полей.

Если нанести (Xi; Yi) на координатную плоскость, то получится график, который наз–ют поле корреляции (или диаграмма рассеивания).

Y

(обозначения оси Y: Y1, Y2, Y3, Yn оси X:X1, X2, X3, Xn)

Построенные точки никогда не будут находится на некоторой гладкой линии типа прямой, параболы и т. д.

Происходит это потому, что на перем–ую Y влияют помимо X другие факторы, либо неучтенные (качество почвы полей), либо случайные (колич–во осадков выпавших в сезоне).

Связь перем–х, на которую накладывается воздействие случайных факторов наз–ся статистической (стохастической).

Формулой статистич. связи Y=f (x, ε)

ε- это случайный фактор или возмущение.

Уравнение регрессии устанавливает причинную взаимосвязь перем–х X иY, в отличии от понятия корреляции, которое устанавливает степень синхронности изменения X иY.

Уравнение регрессии для 2–х перем–х наз–т парной регрессией при большем числе перем–х – уравнением множественной регрессии.

Выбор конкретной формулы связи для 2–х перем–х наз–т спецификацией уравнения регрессии.

Класс мат функций для описания 2–х перем–х достаточно широк.

1. линейная функция y=β0+β1x

2. парабола 2–го порядка y=β0+β1x+β2x²

3. степенная функция y=β0x^β²

4. показательная функция y=β0(β1)^x

5. экспоненциальная функция y=e^ β0+β1x и т.д.

(^-в степени)

Какую из этих зависимостей выбрать для описания связи 2–х перем–х иногда подсказ–т построенное поле корреляции.

Y

Y

Y

Если поле корреляции не дает четкой картины зависимости X и Y (рис 4), то спецификацию уравнения начинают с самой простой формы связи–линейной.

Если в последующем она не устраивает по точности, то ее усложняют, выбирая какие–либо нелинейные модели.

После выбора формы связи м/у перем X и Y приступают к оценке коэф. β0, β1, β2 на основе представленных статистич. данных.

Этот процесс наз–ся параметризацией уравнения регрессии.

№12.Пусть поле корреляции такое, что точки (Xi; Yi) примерно наход–ся на некоторой прямой (рис 2).

Тогда в природе связь м/у перем–ми X и Y явл–ся линейной и уравнение регрессии имеет вид: y=β0+β1x+ε (1)

здесь β0, β1– коэф–ты, которые неизвестны, а ε– случайный фактор возмущения.

Уравнение (1) будем наз–ть модельным уравнением регрессии, т.к. коэф β0, β1 неизвестны, а известны статистич–е данные (Xi; Yi), i=1,n (сверху черточка), то возникает задача оценки по имеющ–х выборки уравнения (1).

Такой оценкой явл–ся выбороч–е ур–е регрессии.

y˜=b0+b1x (2)

Построение ур–ия (2) сводится к определению параметров b0, b1, которые будут точечными оценками коэф β0, β1 соотв–но.

Точечные оценки можно получать различными методамию

*** «Наивный» способ

b1=tgα

Однако этот метод не явл–ся научно–обоснов–ым и дает «плохие» оценки.

В эконометрике наиб–е распостр. для получ–я параметров ур–я регрессии получил МНК.

Этот метод дает «хорошие» оценки не всегда, а при выполнении опред–х условй.

Выборочные знач–ия (Xi; Yi) должны удовлетв–ть ур–ю (1), т. е.

Yi=β0+β1Xi+εi, i=1,n (сверху черточка) (3)

Чтобы МНК дал «хорошие» оценки должны выпол–ся след–е предпосылки МНК относит. ур–я (3).

1. В ур–е (3) возмущение εi явл–ся случ. величинами =, а знач–е перем. Xi – есть не случ. величины.

2. M(εi)=0, i=1,n (сверху черточка)

3. D(εi)=σ²=const

наз–т гомоскедастичностью возмущений (одинаковый разброс)

Если это св–во не выполн–ся, т.е. D(εi)=σi², то это наз–т гетероскедастичностью.

4. M(εi, εj )=0, i ≠ j, т. е. возмущения.

в различных наблюдениях не явл–ся коррелир–ми.

5) εi~N (0, σ²)

Если модель 3 удовл–ет указ–ым предпосылкам, то ее наз–ют нормальной классической линейной регрессионной моделью.

№13.Согласно МНК неизвест–е b0 и b1 выбир–ся таким образом, чтобы сумма квадратов отклонений статистич. значений yi от y˜I опред–х по формуле y˜i=b0+b1xi, i=1,n(сверху черточка) была min.

ei=yi-y˜i – остаток bi наблюд–ии

Сумма квадрат отклон–я Q(b0,b1)=Σ(yi-y˜i)²=Σei²=Σ(yi-b0-b1xi)² (4)

Для нахожд–я min функции 2–х перем–х (4) приравнив–м частные производные по параметрам к 0.

υQ/υb0=0 ; υQ/υb1=0

В итоге получаем след–е формулы для опред–я параметров b0 и b1.

b1= (xy(cчертой) – x(с чертой)*y(с чертой)) /(x²(с чертой) – x(с чертой)^²)

b0=y(с чертой) – b1*x(с чертой) (5)

Формулу (5) наз–т МНК–оценками, здесь

x(с чертой) =1/nΣxi

y(с чертой) =1/nΣyi

xy(с чертой) =1/nΣxiyi

x²(с чертой) =1/nΣxi²

Т.(Гаусса–Маркова):

Если регрессионная модель формулы (3) удовл–ет предпосылкам 1)–4), то МНК оценки имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, т.е. они явл–ся несмещенными и эффективными.

№14.После этапа параметризации линейной парной регрессии было получено

y˜=b0+b1x (1)

Параметр b1 наз–ся выборочным коэф регрессии.

Он показывает на сколько в среднем изм–ся перем–я y, если перем–я x ↑ на 1 ед–цу своего измерения.

В этом эконом смысл параметра b1.

Параметр b0 не имеет спец. названия, как и в об–м случае эконом смысла.

Чисто формально b0 пред–т знач–е перем y при x=0 и если перем–я x не может принимать нулевое знач–е, то и b0 не имеет эконом смысла.

Из эконом смысла b1 следует, что он явл–ся измерителем тесноты связи y и x.

Однако b1 зависит от единиц измер–я y и x.

*** если x измерять не в тоннах, а в кг, то параметр b1 ↓ в 1000 раз. Потому как хар–ка тесноты связи параметр b1 не удобен, для получения хар–ки не завсимой от размер–ти y и x.в кач–ве единиц измер–я берут среднее квадратич–ое отклонение перем–х y и x.

Для этого введем в рассмотрение

σx²=1/n Σ(xi-x¯)²=x²¯- (x¯)²

σy²=1/n Σ(yi-y¯)²=y²¯-(y¯)²

y˜=b0+b1x=y¯-b1x¯+b1x=y¯+b1(x-x¯)

y˜-y¯=b1(x-x¯)

(y˜-y¯)/σy=(b1*σx/σy)*( (x-x¯)/σx)

↓ ↓ ↓

ty rxy tx

ty= rxy*tx (2)

это уравнение парной регрессии в стандартизированном виде, где ty и tx уже не имеет размерности.

rxy= b1*(σx/σy) (3)

Коэф–т rxy наз–ся выборочным коэф–ом парной корреляции.

Он показывает на сколько в сред–м своих квадратич–х отклонений σy изменится y, когда х ↑ на одно свое сред квадрат отклон–е σx.

Св–ва σxy:

1. –1≤ rxy≤1

чем ближе │rxy│к 1, тем теснее связь м/у х и y.

Если rxy>0, то связь прямая, rxy<0, то связь обратная.

Если rxy=1 или rxy=–1. то м/у х и y сущ–ет линейная функциональная связь.

Если rxy=0, то м/у х и y нет никакой связи, y˜=y¯.

Для промежуточных значений rxy сущ–ет след шкала Чеддока по хар–ке связи.

Хар–ка связи: rxy:

слабая 0,1–0,3

умеренная 0,3–0,5

заметная 0,5–0,7

высокая 0,7–0,9

весьма высокая 0,9–0,99

Другой важной хар–ой силы связи фактора х с результатом у явл–ся коэф–т эластичности.

Различают средние точечные (обобщенные и частные) коэф эластичности.

Если перем-е х и у связывают урав–е у˜=f(х), тогда сред коэф эластичности подсчит–ся по формуле Э¯=(df/dx)*(x¯/f(x¯))

В частном случае для модели (1)

Э¯=b1*(x¯/y¯)

Частный коэф–т эластичности некоторой точки х0 вычисл–ся по формуле:

Э0=(df/dx)*(x0/f(x0))

Средний коэф–т эласт–ти показывает на сколько в среднем % изм–ся перем–я у, если перем–я х увелич–ся на 1% от своего сред–го знач–я.

Коэф–т эластичности–безразмерная величина.

№15.В основе проверки значимости ур–я регрессии и его точности наход–ся аппарат дисперсионного анализа.

Центральное место в дисперсионном анализе занимает положение о том, что для линейных моделей об–я сумма квадратов отклонения перем–ой у от своего сред знач–я у¯ пред–ся в виде 2–х частей:

Одна из них вызвана влиянием изуч–го фактора х, а др прочими неучтенными факторами, т. е.

Q=Σ(yi-y¯)² =Σ(yi˜-y¯)² + Σ(yi-yi˜)²

Q = Qr + Qe

Qr– наз–т факторной суммой квадрата и она пред–т объясненную часть измененмя у.

Qe– наз–ют остаточной суммой квадрата, это не объясненная часть.

Если Qr>Qe, то модель явл–ся статистич значимой, т.е. фактор х сущ–но вляет на у.

Если Qr≤Qe, то перем–я х не сущ–но влияет на у и ур–е регрессии не явл–ся статистич значимым.

В связи с этим вводят в рассм–е 1 из эффективных … адекватности линейной регрессионной модели– коэф детерминации.

R²= Qr/Q = 1-(Qe/Q)= 1 – (Σ(yi-yi˜)²/Σ(yi-y¯)²) (4)

R² показывает какая часть (доля) вариации зависимой перем–ой у обусловлена изм–ем перем–ой х из формулы (4) след–т 0≤R²≤1

и чем ближе R к 1, тем лчше данная модель опрокс–ет статистич данные.

Для линейной парной регрессии справедлива след формула:

R²=rxy²

Кроме павенства (5) сущ–ет равенство м/у числами степеней свободы об–ей, факторной и остаточной суммы квадратов.

n-1=1+(n-2)

Поделив факторную и остаточную сумму квадрата на соот–е число степене свободы, получим несмещенные оценки соот–х дисперсий.

Sr²=(Σ(yi˜-y¯)²)/1

S²=(Σ(yi-yi˜)²)/(n-2)

H0: Sr²= S²

Модель статистич не значима при проверке

F= Sr²/ S²=((Σ(yi˜-y¯)²)*(n-2))( Σ(yi-yi˜)²) (6)

которое имеет F–распред Фишера числами степеней свободы k1=1, k2=n-2.

По формуле (6) подсчит–т F набл, а по таблице распред–я Фишера по заданной значимости α число степеней k1, k2 находится F кр.

Если F набл> F кр, то гипотеза H0 отвергается и ур–е признается стастич значимым.

М/у коэф детерминации и F сущ–ет след связь:

F=(R²/(1-R²))*(n-2) (7)

Примечание: Все на ваше усмотрение! В 21 вопрос можно добавить и 22, и 23 вопрос, в лекции это один вопрос. В 22 вопросе примеры приводила из лекции.