49. Аналитическое и механическое выравнивание временного ряда

Если при анализе структуры ВР будет выявлено отсутствие циклической компоненты , то можно непосредственно переходить к моделирования тенденции ВР.

Если же во ВР имеется циклические колебания, то прежде всего из ВР надо исключить циклическую составляющую и лишь затем приступить моделированию тенденции ряда.

Для выявления основной тенденции ВР, т.е.для выравнивания ВР используется различные методы, кот-ый можно разделить на 2 вида:

1. методы механического (алгоритмического) выравнивания.

2. Методы аналитического выравнивания.

Из метода 1-го вида рассм.метод скользящих средних. Он основан на переходе от исходн.уровней ряда y_t, их средним значением на некот.фиксир-ом интервале, длина кот-го заранее определена.

, если m=3,5,7,…(нечётн.) m=2p+1

При переходе к таким средним теряется число уровней ряда.

При m=3, теряется знач. и .

Однако в эконометрике осн-ое внимание удел-ся аналитическому выравниванию. Этот метод заключается в построение аналитической ф-ии, характер-ий зависимость ур-ня ряда от времени, т.е. построение регрессии .

Для этого использ-ся различные ф-ии:

1)линейный тренд ỹ_t=b₀+b₁t

2)параболический тренд ỹ_t=b₀+b₁t+b₂t²

3)степенной тренд ỹ_t=b₀t

и т.д.

В итоге, задача сводится к построению парной регрессии, кот-й в кач-ве независимой переменной исп-ся во времени t, а в качестве завис.перем.ур-нь ряда y_t.

Отметим , здесь задача упрощается, т.к.перем.t принимает только целое значение.

Нелинейные модели тренда проходят предварительную стадию линеаризации для получения оценок параметров МНК.

50. Применение фиктивных переменных при моделировании сезонных колебаний ряда

Если в структуре ВР имеется циклич.колебания, то выравнивание ряда недопустимо, предварительно эти колебания надо исключить из исходной уровни ряда. Рассмотрим это на примере сезонных колебаний ВР.

Один из подходов заключ-ся в расчете значение сезонной компоненты и построений, либо аддитивной y_t =U_t+V_t+E_t модели ряда, либо мультипликативной модели ряда y_t =U_t*V_t*E_{t .}

Аддитивная модель выбирается в тех случаях, когда амплитуда сезонных колебаний со временем изменения времени не изменяется.

y_t =U_t+V_t+E_t

Мультипликат.модель выбир-ся в тех случаях, когда амплитуда сезонных колебаний со временем изм-ся.

y_t =U_t*V_t*E_t

Построение обеих моделей сводится к расчету знач. U_t,V_t,E_t для каждого уровня ряда. Сезонная компонента V_t должны удовлетворять след.условиям:

1)для аддитивной модели сумма всех сезонных компонент за год должна равняться 0.

2)в случае мультипликат.модели произвед-е всех сезонных компонент за один цикл должны ровняться 1.

В итоге, процесс построения модели включает в себя след.шаги.(для аддитивной модели). y_t =U_t+V_t+E_{t .}

1. выравнивание исходных уровней ряда методом скользящей средней. В итоге получается выравненный ряд, не содержит сезонные компоненты.

2. расчет значений сезонной компоненты как разность м/у фактич-ми уровнями ряда и скользящими средними, полученными на первом шаге. Если полученные оценки сезонной компоненты не удовлетворяют приведенным выше требованиям, то они корректируются, чтобы эти требования выполнялись.

3. устранение сезонных компоненты из исходных уровней ряда y_t -V_t =U_t+E_{t .}

4. аналитическое выравнивание уровней ряда U_t,E_t.

5. по получение модели тренда, расчёт +v_t и оценка точечности модели.

Рассмотрим ещё один метод моделировании ВР, содерж-его сезонное колебание. В этом методе на ряду с независимой переменной t включаются фиктивные переменные, число кот-ых на единицу меньше числа периодов времени внутри одного цикла колебания.

Например, при моделировании поквартальных данных помимо перемен. t, исп-ют ещё 3 фиктивн.перемен. например, линейная модель тренд будет иметь вид: .

z_i = 1 для i-го квартал

z_i = 0 для др.кварт.

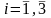
В итоге, для 1-го, 2-го квартала уравнение будет ,

Для 4-го кварт.

В итоге, фиктивные переменные позволяют дифференцировать величину свободного члена уравн.регрессии для кажд.кварт.

Недостаток такого подхода заключается в большом кол-ве переем-х модели.

Например, при описании данных для каждого месяца придется вести в рассмотрение 11 фиктивных переменных и модель становится неудобной для фактического исп-я.