
- •Случайные события. Вероятность. Теоремы сложения и умножения.
- •Случайные величины. Законы распределения дискретных и непрерывных случайных величин
- •Числовые характеристики дискретных и непрерывных случайных величин
- •Системы случайных величин. Законы распределения и числовые характеристики
- •Генеральная и выборочная совокупность. Выборочные характеристики
- •21. Нелинейная парная регрессия. 2 типа нелинейных регрессий.
- •23. Индексы корреляции и детерминации в нелинейных регрессиях.
- •24. Классическая нормальная линейная модель множественной регрессии.
- •28. Коэффициенты множественной детерминации и корреляции
- •29. Оценка значимости уравнения в целом и его параметров в отдельности
- •30. Доверительный интервал для коэффициентов множественной регрессии
- •31. Доверительные интервалы для индивидуальных прогнозных значений зависимой переменной
- •32. Частные f-критерии и их использование в эконометрике
- •33. Мультиколлинеарность, ее разновидности, последствия и способы выявления
- •37. Устранение гетероскедастичности. Взвешенный метод наименьшего квадрата.
- •38. Обобщенная модель множественной регрессии.
- •39. Автокорреляция, ее виды и последствия.
- •40. Методы обнаружения автокорреляции.
- •41.Оценка параметров при наличии автокорреляции.
- •47. Общие понятия временного ряда. Его составляющие. Типы моделей
- •48. Стационарные временные ряды. Коэффициент автокорреляции. Коррелограмма
- •49. Аналитическое и механическое выравнивание временного ряда
- •50. Применение фиктивных переменных при моделировании сезонных колебаний ряда
- •51. Тесты Чоу и Гуйарата для обнаружения структурных изменений ряда
- •Вопрос 52
- •Вопрос 53
39. Автокорреляция, ее виды и последствия.
В общей классической модели множественной регрессии выполнялась четвертая предпосылка М(Еi, Еj)=0 i≠j, т.е. cov(Еi, Еj)=0 - были некоррелируемые. На практике это условие не всегда выполняется.
Автокорреляция определяется как корреляция между показателями упорядоченными либо в пространстве, либо во времени (временные ряды).
Под автокорреляцией случайных составляющих Еi будем понимать корреляционную зависимость между Еi и значением Еi-l, где l- величина сдвига по номеру наблюдения; при l=1 будет автокорреляция Е в соседних наблюдениях.
Различают положительную и отрицательную автокорреляции. Положительную автокорреляцию рассмотрим на след примере.
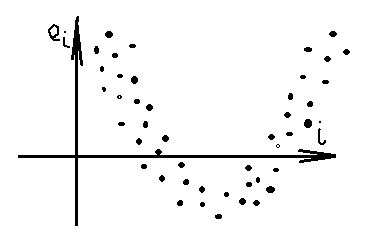
Пусть изучается модель зависимости спроса у на мороженое (по ежемесячным данным на протяжении нескольких лет) от дохода х семьи. Будем предполагать, что состояние погоды является единственным фактором скрытым в возмущении Е. Тогда поле корреляции будет иметь след вид:
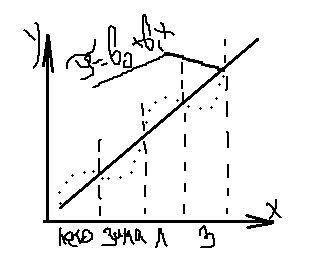
Графическое
изображение автокорреляции выражается
в данном примере в чередовании зон, где
наблюдаемое значение уi
расположены выше предсказанной модели
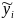 ,
и зон где наблюдаемое значение у находится
ниже расчетного значения
.
Это характерно для положительной
автокорреляции.
,
и зон где наблюдаемое значение у находится
ниже расчетного значения
.
Это характерно для положительной
автокорреляции.
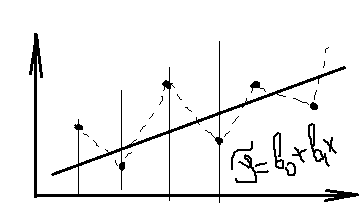
Отрицательная
автокорреляция встречается в тех
случаях, когда последовательное
наблюдение действует друг на друга по
принципу маятника. Завышенное значение
уi по сравнению
приводит к занижению значения уi+1
по сравнению
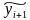 в последующем наблюдении и наоборот.
в последующем наблюдении и наоборот.
В экономических процессах автокорреляция встречается достаточно редко.
Последствия автокорреляции очень похожи с отрицательными последствиями гетероскедастичности:
оценки параметров перестают быть эффективными
оценки дисперсии становятся смещенными S2=
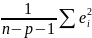 M(S2)≠D(Ei)=σ2
M(S2)≠D(Ei)=σ2стандарсные ошибки становятся заниженными mbj, что приводит к завышению tстатистик tbj, отсюда следует неправильный вывод о статистической значимости параметров.
40. Методы обнаружения автокорреляции.
Разработано несколько способов для обнаружения автокорреляции. Самым простым является графический метод. Остатки еi=yi+ является оценкой случайных составляющих Еi, поэтому если корреляция ошибок регрессии =0, то она отсутствует и в остатках регрессии и это обнаруживается при построении графиков зависимости еi от номера наблюдения i.
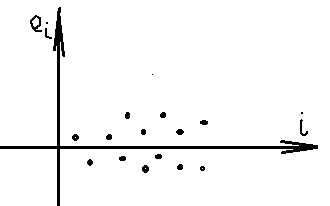 автокорреляция
отсутствует
автокорреляция
отсутствует
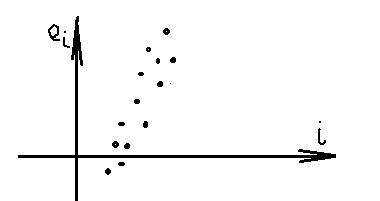 автокорреляция
присутствует
автокорреляция
присутствует
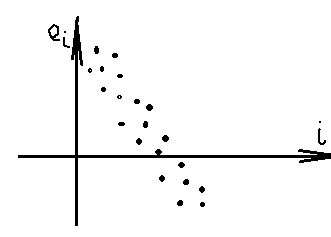 автокорреляция
присутствует
автокорреляция
присутствует
 автокорреляция присутствует
автокорреляция присутствует
Для обнаружения автокорреляции используют статистические тесты. Наиболее простым является тест Дарбина-Уотсона. Этот тест используется для обнаружения автокорреляции первого порядка, когда автокорреляция подчиняется уравнению Еi=ρEi-1+ηi (1) ρ- коэффициент корреляции
cov(ηi; ηj)=0
если ρ>0- положительная автокорреляция
если ρ<0- отрицательная автокорреляция
если ρ=0- автокорреляция отсутствует
Уравнение (1) поскольку оно связывает возмущения в соседних наблюдениях называют уравнением авторегрессии 1го порядка.
В тесте Дарбина-Уотсона тестируется гипотеза H0: ρ=0
Для проверки этой гипотезы используют статистику Дарбина-Уотсона (DW=d)
DW=d= (2)
(2)
Оценкой коэффициента корреляции ρ является r, который вычисляется:
r=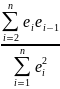 (3) n-велико
(3) n-велико
d≅2(1-r) (4)
Из формулы (4) видно, что если r=0, то d→2, если r=1, то d→0, если r=-1, то d→4.
Критическое значение для статистики DW, т.е. dкр зависит от n, числа параметров модели р, хi (значений объясняющих переменных), поэтому таблицы, аналогичные t-статистикам, F-статистикам здесь рассчитывать невозможно, но можно вычислить верхнюю dв (du) и dн(dl)- нижнюю критическую границу статистики DW, которая находится α, р, n.
Схема критерия DW следующая:
по формуле (2) находится значение статистики DW dнаб
из таблицы находим dв и dн. Для облегчения находим строим следующий график.
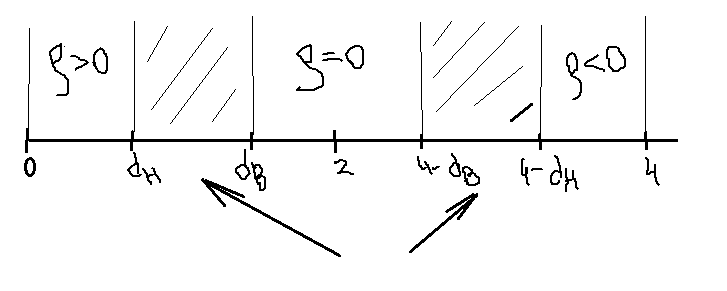
зоны неопределенности
Недостатки теста DW:
этот тест нельзя использовать для моделей без свободных слагаемых b0
данный метод проверяет наличие автокорреляции 1го порядка
уверенные результаты получаются при больших выборках
наличие зон неопределенности.
