3.3 Кинематика и динамика жидкостей

Кинематикой жидкости называется раздел механики, в котором изучаются геометрические свойства механического движения жидкости без учета их массы и действующих на них сил.

Основными уравнениями, позволяющими решать простейшие задачи о движении жидкости под давлением, являются уравнение постоянства расхода (равенство расхода Q во всех сечениях установившегося потока) и уравнение Бернулли.

Уравнение неразрывности может быть представлено в виде

Q = V₁ ₁ = V₂ ₁ = . . . = V_n _n = const, (3.27)

Из него следует, что средние скорости обратно пропорциональны площадям живых сечений

, (3.28)

Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока.

Для двух сечений элементарной струйки имеет вид

, (3.29)

где Z – вертикальные координаты центров тяжести и сечений (удельная энергия положения), м;

– пьезометрическая высота (удельная энергия давления), м;

– скоростная высота (напор) – удельная кинетическая энергия, м;

Н – полный напор или полная удельная энергия, м.

Для установившегося движения потока реальной жидкости оно является уравнением баланса энергии с учетом гидравлических потерь и имеет вид

(3.30)

где V – cредняя по сечению скорость, м/с;

 – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям и равный отношению действительной кинетической энергии потока к кинетической энергии того же потока, но при равномерном распределении скоростей по сечению;

h – гидравлические потери между сечениями 1 и 2, обусловленные вязкостью жидкости и другими факторами, м.

Гидравлические потери состоят из потерь на трение h_тр и местных потерь h_м, т.е.

h = h_тр + h_м. (3.31)

Местные потери возникают в местных гидравлических сопротивлениях, т.е. там, где изменяются форма и размеры русла, и определяются по формуле Вейсбаха

, м (3.32)

где V – средняя скорость потока в сечении перед местным сопротивлением, м/с;

 – безразмерный коэффициент местного сопротивления.

Значение коэффициента  определяется формой местного сопротивления, его геометрическими параметрами. Режим движения потока жидкости определяется числом Рейнольдса

(3.33)

где  – кинематическая вязкость жидкости, выражаемая в [м²/с].

Для некруглых труб

, (3.34)

где . Здесь ω – площадь живого сечения; χ – смоченный периметр. Для круглых труб d = 4R_Г.

При Re < Re_кр, где Re_кр = 2300, режим движения ламинарный – при котором отсутствует перемешивание жидкости, пульсации скорости и давления.

При Re > Re_кр режим движения турбулентный, т.е. с интенсивным перемешиванием и вихреобразованием жидкости, с пульсацией скоростей и давлений.

Потери напора на трение определяются по формуле Дарси-Вейбаха

[Па] (3.35)

где  – коэффициент гидравлического трения.

При ламинарном режиме  определяется как

 = 64 / Re, (3.36)

а формула Дарси превращается в формулу Пуазейля

, [м] (3.37)

Коэффициент Кориоллиса  в уравнении Бернулли при ламинарном потоке принимается  = 2.

Для труб, работающих как “гидравлически гладкие”,  определяется по формуле Блазиуса

. (3.38)

При турбулентном режиме , кроме числа Рейнольдса, зависит еще от относительной шероховатости /d, т.е.

_т = f (Re, /d).

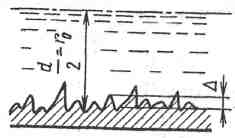Величину /d (или /r₀) называют относительной шероховатостью, a обратную величину d / – относительной гладкостью.

Рисунок 3.4 – Характерные геометрические параметры потока в круглой трубе

Для реальных технических труб с естественной шероховатостью для определения  рекомендуется формула А.Д.Альтшуля

. (3.39)

где _э – эквивалентная шероховатость трубы, мм.

Эквивалентная шероховатость  представляет собой выступы равномерно распределенной зернистой абсолютной шероховатости такого размера, при котором потери напора будут такими же, как и при действительной шероховатости.

При малых значениях (Re ) вторым слагаемым можно пренебречь, и (3.39) обращается в (3.38). Наоборот, при больших (Re ) первое слагаемое делается ничтожно малым и формула (3.39) преобразуется в формулу Б. Шифринсона:

(3.40)

Во всех случаях турбулентного потока коэффициент Кориоллиса  в уравнении Бернулли принимается равным  = 1.

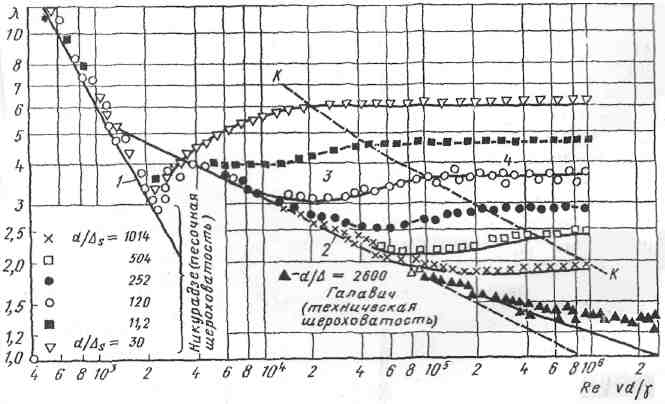
И. Никурадзе (1933 г.) впервые обработал свои многочисленные опытные результаты указанным способом и построил универсальную зависимость (рис. 3.5). Шероховатость в опытах Никурадзе создавалась искусственно путем наклеивания калиброванных песчинок на внутреннюю поверхность трубы. Такая шероховатость получалась равнозернистой, чем существенно отличалась от естественной шероховатости труб, образующейся в результате коррозии, отложений и т. п.

Рассмотрим подробно график Никурадзе. Логарифмические шкалы на осях координат выбраны для того, чтобы сделать его наиболее компактным. На поле графика можно отметить четыре характерные зоны.

1. Зона ламинарного режима, изображаемая прямой. Точки, относящиеся к опытам, проведенным при разной шероховатости, ложатся, на одну прямую, уравнение которой

₁ = 64/Re.

Следовательно, в пределах этой зоны λ зависит только от числа Re и не зависит от шероховатости стенок трубы. Границей зоны служит значение абсциссы lg 2300 = lg Re_Kp. Таким образом, данная закономерность имеет место при Re < Re_Kp, т. е. при ламинарном режиме течения в трубе. При этом потери линейно зависят от скорости.

Рисунок 3.5 – Экспериментальная зависимость гидравлического коэффициента трения К от числа Рейнольдса Re и относительной гладкости d/_s при песочой шероховатости (график Никурадзе)

В диапазоне чисел Re = 2300 ... 4000 осуществляется переход от ламинарного режима течения к турбулентному. В потоке наблюдается неустойчивость, порождаемая периодическим возникновением очагов турбулентности и их исчезновением.

2. При турбулентном режиме движения и гидравлически гладких трубах, независимо от их шероховатости, все точки располагаются на прямой 2, называемой зоной гладкостенных труб, описываемой формулой Блазиуса

λ = 0,3164 / Re ^0,25.

При турбулентном течении вблизи стенки сохраняется вязкий подслой, движение в котором преимущественно ламинарное. Толщина подслоя δ_Л достаточна, чтобы покрыть все неровности стенки благодаря чему турбулентное ядро потока движется как бы в гладкой трубе. Трубы, работающие в таком режиме, иногда называют гидравлически гладкими.

3. Зона доквадратичного сопротивления, которая ограничивается линией гладкостенного режима и штриховой линией КК (см. рис. 3.5), образованной точками, отделяющими горизонтальные участки кривых. Можно видеть, что в зоне 3 каждая кривая соответствует определенному значению относительной гладкости. Здесь имеет место наиболее общий случай:

λ₃ = λ₃ (Re, d /₃).

4. Зона квадратичного сопротивления, образуемая горизонтальными участками кривых. Очевидно, здесь коэффициент λ не зависит от Re, т.е.

λ₄ = λ₄ (d /).

В этой зоне для труб с искусственной равномерно-зернистой шероховатостью λ вычисляют по формуле И. Никурадзе

.