Результаты расчета всех гармоник
Номер гармоники k |
Длина волны L/k |
Коэффициент |
Ампли-туда A |
Дисперсия отклонений D(o,k) |
Дисперсия гармоник |
||||
аk |
bk |
D(k) |
D(k),% |
||||||
0 |
– |
3,140 |
0,000 |
0,000 |
2,790 |
0,000 |
0,0 |
||
1 |
24,0 |
0,335 |
–0,058 |
0,340 |
2,734 |
0,056 |
2,0 |
||
2 |
12,0 |
–0,376 |
0,054 |
0,380 |
2,665 |
0,070 |
2,5 |
||
3 |
8,0 |
–1,828 |
0,535 |
1,905 |
0,912 |
1,753 |
62,8 |
||
4 |
5,0 |
–0,154 |
–0,070 |
0,169 |
0,898 |
0,014 |
0,5 |
||
5 |
4,8 |
0,084 |
0,040 |
0,093 |
0,894 |
0,004 |
0,2 |
||
6 |
4,0 |
0,597 |
–0,883 |
1,066 |
0,317 |
0,577 |
20,7 |
||
7 |
3,4 |
0,469 |
0,042 |
0,471 |
0,210 |
0,107 |
3,8 |
||
8 |
3,0 |
0,241 |
0,178 |
0,300 |
0,166 |
0,044 |
1,6 |
||
9 |
2,7 |
–0,041 |
0,128 |
0,135 |
0,156 |
0,009 |
0,3 |
||
10 |
2,4 |
–0,146 |
0,263 |
0,301 |
0,110 |
0,046 |
1,7 |
||
11 |
2,2 |
–0,243 |
0,326 |
0,406 |
0,027 |
0,084 |
3,0 |
||
12 |
2,0 |
–0,088 |
0,000 |
0,088 |
0,027 |
0,000 |
0,0 |
||
|
|
|
|
|
|
|
|
||
Сумма |
– |
– |
– |
– |
– |
2,764 |
99,1 |
||
Результаты расчетов по всем 12 гармоникам суммированы в табл.5.8. Отметим, что отношение L/k – это длина волны гармоники k. В таблице приведены длина волны, коэффициенты ak и bk, амплитуда А, дисперсии отклонений D(o,k), их разности – дисперсии гармоник D(k) и они же, выраженные в процентах от дисперсии пространственной переменной.
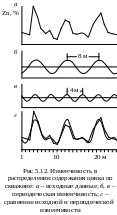
Вычисления показали, что главное значение имеют третья гармоника с длиной волны 8 м (рис.5.12, б), ее доля составляет 62,8 %, и шестая гармоника с длиной волны 4 м (рис.5.12, в), ее доля 20,7 %. Остальные гармоники играют малую роль.
Следовательно, можно ограничиться двумя важнейшими гармониками, которые в сумме дают 83,5 % от дисперсии пространственной переменной (рис.5.12, г).
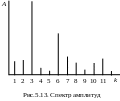
Данные табл.5.8 позволяют построить спектр амплитуд (рис.5.13).
5.4.3. Периодограммный анализ
Периодическая изменчивость не обязательно должна быть синусоидальной, она может иметь любую форму. Можно выявить периодическую изменчивость любой формы путем последовательного перебора длин волн, кратных шагу наблюдений. Такая методика, по-видимому, не описана в литературе. Предлагается назвать ее периодограммным анализом.