- •1.1. Геологические объекты и их свойства
- •Характеристика текстуры руды
- •1.2. Понятие о математическом моделировании
- •2.1. Одномерная статистическая модель
- •Содержание никеля в руде х
- •Расчет начальных моментов случайной величины
- •Расчет центральных моментов случайной величины
- •Частота и частость содержания железа в руде
- •Расчет статистических характеристик по сгруппированным данным (по данным гистограммы рис.2.1)
- •2.2. Законы распределения случайных величин
- •Функции нормального распределения
- •Функция распределения Стьюдента Fk (t) в зависимости от числа степеней свободы k
- •Плотность вероятности распределения Стьюдента fk(t) в зависимости от числа степеней свободы k
- •Коэффициенты вероятности t распределения Стьюдента при заданной вероятности и степени свободы k
- •Коэффициенты вероятности распределения 2 при заданных вероятности и числе степеней свободы k
- •Расчет графика плотности вероятности нормального закона
- •Подбор функции преобразования случайной величины х (содержание TiO2 в магнетите)
- •2.3. Геологические приложения
- •Пример выявления аномальных значений
- •Результат вычисления истинных характеристик
- •3.1. Двухмерная статистическая модель
- •Расчет коэффициента корреляции
- •Расчет параболической зависимости, аппроксимирующей изменение мощности рудного тела
- •Сравнение фактической и расчетной (теоретической) мощности
- •Дисперсии отклонений
- •3.2. Геологические приложения двухмерной статистической модели
- •Расчет случайной погрешности химического анализа
- •Расчет систематической погрешности анализов серы
- •Результаты опытов по измерению радиоактивности препарата
- •Содержание железа в руде и плотность руды
- •Расчет частот n
- •4.1. Многомерная статистическая модель
- •Расчет статистических характеристик многофакторной зависимости
- •Сравнение фактических и расчетных содержаний золота
- •Химические анализы проб руды
- •Матрица коэффициентов корреляции
- •Состав магнетита, %
- •Преобразованная матрица коэффициентов корреляции
- •Матрица коэффициентов корреляции
- •Расчет первого собственного числа
- •Расчет матрицы коэффициентов первого фактора
- •Первая остаточная матрица коэффициентов корреляции
- •Факторные нагрузки
- •Нормированный состав магнетита
- •Главные компоненты z
- •Средний состав групп магнетита, %
- •Состав циркона, %
- •Сложные признаки
- •Результаты распознавания объектов
- •Результаты измерения мощности рудного тела
- •Данные по скважинам
- •5.4. Вероятностные модели
- •Результаты измерения мощности рудного тела
- •Значения пространственной переменной
- •Содержание молибдена, %
- •Сглаживание исходных данных
- •Результаты измерений пространственной переменной и некоторые вычисленные данные
- •Результаты расчета всех гармоник
- •Расчет периодической изменчивости
- •Дисперсия различных длин волн
- •5.5. Основы геостатистики
- •Содержание золота в пробах, г/т
- •Данные для кригинга, м
- •Значения вариограммы (h)
- •Реестр разведочных скважин
- •Замеры искривлений скважин
- •Банк данных геологической документации
- •Банк опробования рядовых проб
- •Координаты пунктов искривлений
- •Банк рудных пересечений
- •Банк геологических границ
- •Глава 1. Общие сведения 7
- •Глава 2. Одномерная статистическая модель и ее применение в геологии 23
- •Глава 3. Двухмерная статистическая модель и ее применение в геологии 78
- •Глава 4. Многомерная статистическая модель и ее применение в геологии 115
- •Глава 5. Математическое моделирование пространственных геологических закономерностей 159
- •Глава 6. Основы математического моделирования месторождений 203
Таблица 5.3
Номер
пункта
х,
м
,
м
Номер
пункта
х,
м
,
м
1
0
1,8
16
30
2,1
2
2
1,5
17
32
1,9
3
4
1,6
18
34
1,6
4
6
1,8
19
36
1,4
5
8
1,9
20
38
1,3
6
10
2,2
21
40
1,7
7
12
2.5
22
42
1,9
8
14
2,4
23
44
2,1
9
16
2,4
24
46
2,2
10
18
2,6
25
48
1,5
11
20
2,4
26
50
1,8
12
22
2,2
27
52
2,0
13
24
1,8
28
54
2,3
14
26
1,7
29
56
1,8
15
28
1,9
30
58
1,5
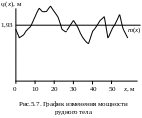
Результаты измерения мощности рудного тела
Пример 5.5. Имеются измерения мощности рудного тела, произведенные через 2 м (табл.5.3). Требуется рассчитать характеристики стационарной случайной функции.
Графический анализ (рис.5.7) показывает, что в поведении мощности отсутствует заметный тренд, поэтому можно принять модель стационарной случайной функции. Математическое ожидание стационарной случайной функции постоянно и равно среднему значению мощности m(x) = = 1,93 м. Дисперсия отклонений равна обычной дисперсии D(x) = 0,117. График автокорреляционной функции (рис.5.8) показывает, что имеются небольшие периодические колебания в исходных измерениях с длиной волны порядка 11 м, а радиус автокорреляции R = 10,43 м.