5.4. Вероятностные модели

ГЕОЛОГИЧЕСКИХ ПОЛЕЙ

5.4.1. Модель на основе случайной функции

Основой случайной функции служит предположение, что измеренные значения являются случайными функциями координат и содержат две составляющие: математическое ожидание m(x) (закономерная изменчивость, или тренд) и случайные колебания (x) относительно его [см. формулу (5.2)].

Если математическое ожидание – величина постоянная, то случайная функция называется стационарной, в противном случае – нестационарной. Математическое ожидание позволяет прогнозировать значения пространственной переменной между пунктами измерений, тогда как случайные колебания служат для оценки погрешности прогнозирования.

Стационарная случайная функция может обладать еще одним свойством. Если на любом ее отрезке характеристики одинаковые, то функция эргодичная, что редко используется в геологической практике.

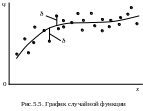
Измеренные значения в отдельных точках называются реализациями случайной функции. Случайную функцию можно изобразить на графике, на котором точки пунктов измерений имеют случайные отклонения  от плавной линии математического ожидания m(x) (рис.5.5). Отклонения бывают положительные, отрицательные и нулевые.

Случайная функция имеет три главные характеристики: математическое ожидание, дисперсию случайных колебаний и автокорреляционную функцию.

Математическое ожидание может рассматриваться как тренд, заданный на основе теоретических соображений (зависимость плотности от состава руды, кривая радиоактивного распада) или эмпирическим способом, чаще всего в виде полинома. Эмпирический полином является приближенной оценкой математического ожидания. Вычисление тренда осуществляется по методу наименьших квадратов (см. подраздел 3.1.5), а наилучший порядок полинома находят согласно подразделу 4.1.3. Возможен еще один метод оценки математического ожидания путем сглаживания исходных данных способом скользящего окна.

Математическое ожидание стационарной случайной функции, как отмечалось, величина постоянная и равная среднеарифметическому из всех измеренных значений. Если из нестационарной случайной функции вычесть математическое ожидание, то, согласно формуле (5.2), она превратится в стационарную с нулевым математическим ожиданием. Во многих случаях математическое ожидание (закономерная изменчивость, или тренд) слабо проявлено, тогда им пренебрегают, полагая случайную функцию стационарной.

Дисперсия случайной функции равна дисперсии отклонений (х):

. (5.10)

Если из дисперсии извлечь квадратный корень, то можно получить среднеквадратичное отклонение _.

Автоковариационная функция

, (5.11)

где m – количество слагаемых под знаком суммы; h – шаг измерений.

Особый интерес представляет автокорреляционная функция

. (5.12)

Она является аналогом коэффициента корреляции случайных величин, колеблется в пределах от –1 до +1 и характеризует зависимость между отклонениями  на расстоянии h.

Автокорреляционная функция зависит от шага измерений h. При нулевом шаге она равна единице, при увеличении шага убывает, приближаясь к нулю. В идеальном виде функция показана на рис.5.6. Шаг, при котором автокорреляционная функция неотличима от нуля, называется радиусом автокорреляции R. Он является важной величиной, характеризующей радиус влияния отдельного измерения.

Следует отметить, что шаг и радиус автокорреляции являются векторными величинами. В изотропной среде радиус влияния одинаков по всем направлениям. В анизотропной среде, а геологические объекты – большей частью анизотропные тела, радиус автокорреляции зависит от направления. Чем сильнее проявлена изменчивость в каком-либо направлении, тем меньше радиус автокорреляции.