Расчет частот n

Класс х, %	Частоты			Класс х, %	Частоты
	фактические	расчетные	округленные		фактические		расчетные		округленные
14-15	–	0,1	–	24-25	31		34,2		34
15-16	–	0,3	–	25-26	25		26,6		27
16-17	–	1,0	1	26-27	22		17,8		18
17-18	–	2,7	3	27-28	8		10,2		10
18-19	–	6,2	6	28-29	5		5,0		5
19-20	–	12,0	12	29-30	–		2,1		2
20-21	–	20,1	20	30-31	–		0,8		1
21-22	29	28,9	29	31-32	–		0,2		–
22-23	35	35,6	36	32-33	–		0,1		–
23-24	40	37,6	38
			Cумма		195		241,5		242

После деления сумм на n найдем моменты: m₁₀ = 3,5692307; m₂₀ = 16,17436; m₃₀ = 84,89231; m₄₀ = 490,20512; m₀₁ = 3,329513; m₁₁ = 11,31389; m₂₁ = 48,29086. Далее вычисляем вспомогательные величины: a₁ = –0,1659145; a₂ = –0,2047645; b₁ = 8,415905; b₂ = 7,907624. Зная их, определим характеристики распределения: = 6,5416; _х= 2,5577; = 2,8685; lnN = 5,4876; N = e^5,4876 = 241,68. Промежуточные расчеты полезно выполнять без округления, иначе при нахождении многочисленных разностей, имеющихся в формулах, точность расчетов заметно снизится.

Так как округленно N = 242, то полная гистограмма должна содержать 242 значения, фактически же имеется 195, следовательно, не хватает 47 значений. Чтобы узнать, в каких классах они должны быть, нужно найти расчетные частоты по формуле (3.41) и сравнить их с фактическими (табл.3.9). По расчетным значениям построена кривая частот нормального закона (рис.3.12), которая хорошо аппроксимирует гистограмму.

МНОГОМЕРНАЯ

СТАТИСТИЧЕСКАЯ МОДЕЛЬ

И ЕЕ ПРИМЕНЕНИЕ В ГЕОЛОГИИ

Г лава 

4.1. Многомерная статистическая модель

4.1.1. Система множества случайных величин

и ее статистические характеристики

Дальнейшим развитием двухмерной статистической модели служит многомерная статистическая модель, которая состоит из совокупности множества сопряженных случайных величин (называемых многомерными случайными векторами) и выражается матрицей свойств размером k  n:

, (4.1)

где n – число наблюдений; k – число свойств.

В основе многомерной статистической модели лежит гипотеза о том, что измеренные значения являются независимыми случайными величинами (векторами), т.е. строки матрицы можно располагать в любом порядке. Однако между столбцами матрицы связь может присутствовать. В ряде задач некоторые из измерений могут быть неслучайными величинами, например заранее заданными пространственными или временны́ми координатами, что не является препятствием для статистической обработки.

Для изображения множества случайных величин используется многомерное признаковое пространство, имеющее k осей. Каждое отдельное измерение (строка матрицы) изображается в таком пространстве точкой, а их совокупность, т.е. матрица (4.1), – облаком точек.

Многомерная статистическая модель имеет различные статистические характеристики, наиболее употребительными из которых являются средние значения случайных величин …, их дисперсии  …,  и среднеквадратичные отклонения ₁, ₂, …, _k. Кроме того, часто используются матрицы ковариации и коэффициентов корреляции случайных величин. Напомним, что ковариация K_ij – это корреляционный смешанный момент двух случайных величин i и j. Матрица ковариации имеет симметричный вид:

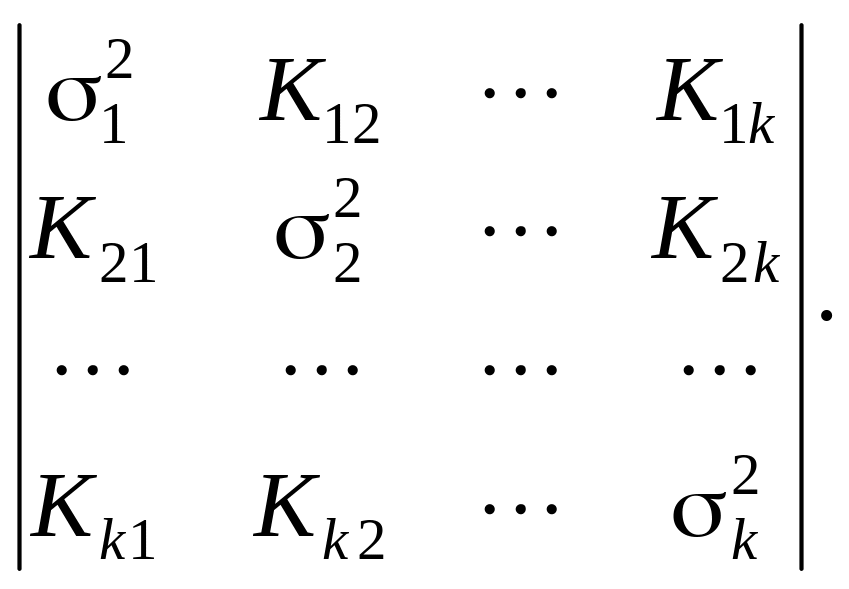(4.2)

В ней по диагонали расположены дисперсии случайных величин, а в остальных полях – корреляционные моменты. Матрица коэффициентов корреляции между свойствами (их называют парными коэффициентами корреляции) также имеет симметричный вид:

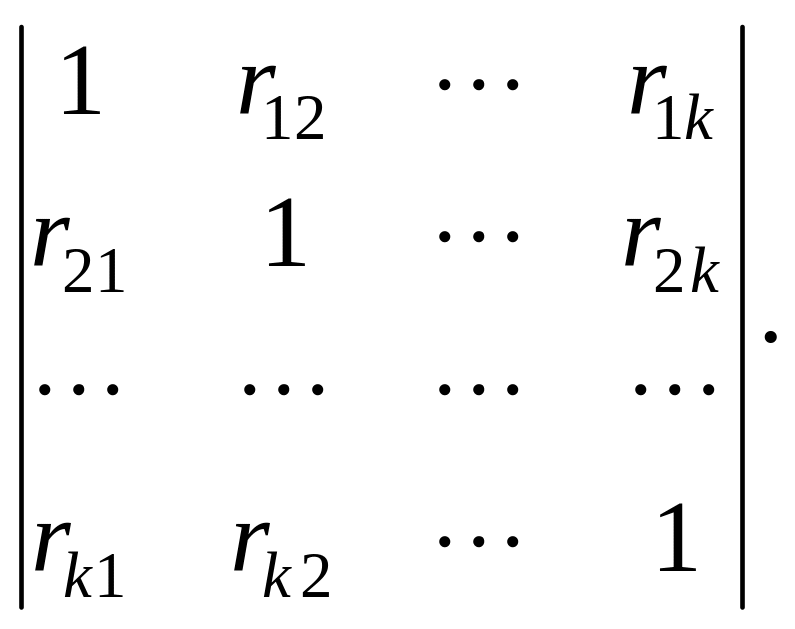(4.3)

В матрице по диагонали находятся единицы, а в остальных полях – собственно коэффициенты корреляции. Методика расчета корреляционных моментов и коэффициентов корреляции такая же, как в двухмерной статистической модели. Данные матрицы коэффициентов корреляции могут быть представлены в виде графа связей (рис. 4.1). Для построения графа использованы результаты силикатного анализа горных пород. Чем больше коэффициент корреляции между компонентами, тем толще соединяющая их линия.

4.1.2. Множественная линейная регрессия. Коэффициент множественной корреляции

Во многих случаях возникает необходимость изучить зависимость одной случайной величины от множества других случайных величин. Многофакторная зависимость обычно выражается уравнением множественной линейной регрессии

y = a₁x₁ + a₂x₂ +  + a_kx_k + b, (4.4)

где x₁, x₂, …, x_k – свойства; a₁, a₂, …, a_k, b – постоянные коэффициенты.

Коэффициенты находят методом наименьших квадратов или через значения статистических характеристик. Результат не зависит от способа вычислений. По второму способу переменные x₁, x₂, …, x_k нормируют по формуле (2.24), т.е. заменяют величинами:

(4.5)

В результате замены уравнение (4.4) приобретет следующий вид:

, (4.6)

где величины А₁, А₂, …, А_k – нормированные коэффициенты регрессии.

Если в формулу (4.6) подставить нормированные значения (4.5), получим выражение множественного уравнения регрессии еще в одной форме:

(4.7)

Заметно сходство уравнений (3.12) и (4.7). В уравнении (4.7) находится несколько однотипных слагаемых, а вместо коэффициента корреляции r присутствуют нормированные коэффициенты регрессии А₁, А₂, …, А_k. Значения А₁, А₂, …, А_k находят путем решения системы линейных уравнений, составленной из коэффициентов корреляции:

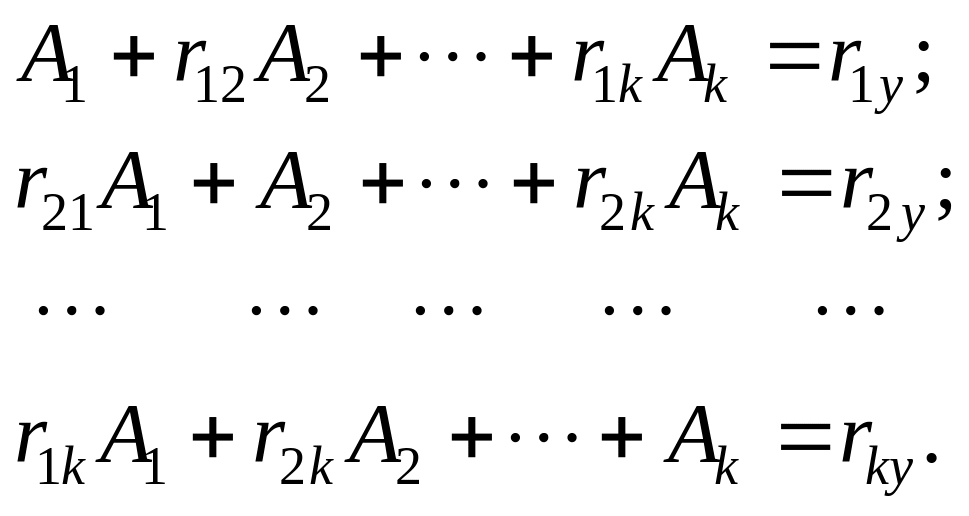(4.8)

Сравнение фактических у и расчетных у_рас значений по уравнению (4.7) дает отклонения . Рассчитав дисперсию отклонений и дисперсию исходных данных , можно найти коэффициент множественной корреляции R, который характеризует степень зависимости свойства у от множества других случайных величин x₁, x₂, …, x_k:

. (4.9)

Значения R колеблются от нуля до единицы. Чем ближе R к единице, тем более сильная зависимость величины у от множества величин x₁, x₂, … , x_k. Кроме того, дисперсия отклонений позволяет рассчитать погрешность уравнения множественной регрессии (при вероятности q = 0,95 и коэффициенте вероятности t = 2), которая равна t_.

Пример 4.1. В табл.4.1 приведены содержания меди, цинка и золота. Необходимо выполнить статистические расчеты.

Имея начальные моменты и формулы перехода от них к центральным моментам (2.14) и далее к статистическим характеристикам (2.15), найдем

Таблица 4.1