Таблица 3.4

Дисперсии отклонений

n	k
0	1	0,08346	0,9527
1	2	0,07835	0,1044
2	3	0,01745	0,0279
3	4	0,01569	0,0314
4	5	0,01039	0,0277
5	6	0,00949	0,0380

Количество степеней свободы k равно количеству постоянных коэффициентов в аппроксимирующей функции, в которой n – число наблюдений. Так, в квадратной параболе (3.27) три постоянных коэффициента, в параболе пятого порядка шесть коэффициентов, в синусоиде три коэффициента и т.д. При исследовании полинома повышают его порядок, начиная с m = 0, и анализируют дисперсию отклонений с учетом использованных степеней свободы k = m + 1. Как только остаточная дисперсия отклонений достигнет минимума, оптимальный порядок полинома получен, дальнейшее его повышение приведет к увеличению данной дисперсии. Для условий примера 3.3 наилучшая функция, аппроксимирующая исходные данные, – это полином четвертой степени (n = 4), что подтверждается данными табл.3.4.

3.1.8. Приведение нелинейных зависимостей

к линейному виду

Система уравнений (3.28), возникающая в результате применения метода наименьших квадратов к нелинейным зависимостям, лишь в редких случаях может быть решена алгебраическим путем. Простое решение системы возникает в случае полиномиальной зависимости. Система уравнений (3.28) для полиномов всегда является линейной. Поэтому по возможности стараются привести сложные для расчета зависимости к линейному или полиномиальному виду.

Например, показательная функция у = ае^bx может быть приведена к линейному виду путем логарифмирования lny = lna + bx и замены переменной z = lny, что приведет к линейному уравнению регрессии z = lna + bx. Здесь неизвестными являются коэффициенты lna и b. Существенно то, что отклонения  рассчитываются не от исходных значений у, а от их логарифмов, что не одно и то же.

Аналогично приводится к линейной логарифмическая функция y = a + blnx путем замены переменной z = lnx, что дает уравнение y = a + bz.

Гиперболическая функция y = a/(1 + bx) приводится к общему знаменателю у + bxy = a, а потом делается замена z = xy. Получим линейную зависимость у + bz = a, обработка которой позволяет найти коэффициенты a и b. Подобные примеры можно продолжить и далее.

3.2. Геологические приложения двухмерной статистической модели

3.2.1. Прогнозирование свойств по уравнению регрессии

Выше отмечалось, что уравнение линейной регрессии позволяет прогнозировать одно свойство по другому, что имеет значение, если прямое измерение характеристики прогнозируемого свойства затруднено или связано с дополнительными затратами. Например, на одном из полиметаллических месторождений установлена линейная зависимость содержания кадмия от содержания цинка в руде (рис.3.7). Коэффициент корреляции между содержаниями 0,937, т.е. очень высокий. Разброс точек на рисунке обусловлен, во-первых, колебаниями состава сфалерита, во-вторых, значительной случайной погрешностью определения содержания кадмия.

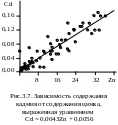
Погрешность уравнения регрессии составляет 0,034 %, что ниже среднего содержания кадмия 0,058 %. Возможно, погрешность уравнения завышена из-за неизбежной случайной погрешности химического анализа (или опробования).

3.2.2. Выявление аномальных значений и однородных совокупностей

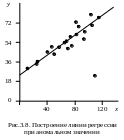
При построении графиков регрессии отдельные точки нередко далеко отходят от линии регрессии (рис.3.8). Без каких-либо расчетов можно считать, что удаленная точка соответствует аномальному значению. Если же точка аномального значения находится вблизи линии регрессии, то необходим специальный расчет. Вначале рассчитывается линия регрессии без предполагаемого аномального значения, далее находят отклонения  точки от линии регрессии и с помощью различных критериев, рассмотренных в подразделе 2.3.3, решается вопрос об аномальности исследуемого значения. Следует отметить, что отклонения  от линии регрессии обычно подчиняются нормальному закону, хотя исходные данные могут существенно отличаться от него. Возможен случай, когда на графике наблюдаются два облака точек, которым соответствуют различные линии регрессии (см. рис.3.1, е), что свидетельствует о неоднородности совокупности значений. Их нужно разделить на две самостоятельные совокупности и обрабатывать раздельно. Выделение однородных совокупностей решается геологическими методами, так как математические методы весьма сложны и в данном учебнике не рассматриваются.

3.2.3. Внутренний контроль химических анализов

Одним из возможных способов применения двухмерной статистической модели является внутренний контроль химических анализов. Однако подобная методика может быть использована также для контроля опробования, минералогического, спектрального анализа и пр.

В основе внутреннего контроля лежит условие равноточности основных и повторных анализов. Пробы делят на две партии и анализируют в одной и той же лаборатории, в одно и то же время и по одинаковой технологии. Первую партию называют основными пробами, вторую – контрольными. Контрольные пробы зашифрованы, так что их нельзя отличить от основных. Сравнение результатов анализов основных и контрольных проб позволяет оценить случайную погрешность анализов (ошибку воспроизводимости анализов). Вначале находят абсолютную случайную погрешность:

, (3.32)

где х и у – соответственно основные и контрольные анализы; n – число контрольных проб.

Далее определяют относительную случайную погрешность, которую обычно выражают в процентах:

. (3.33)

Для относительных случайных погрешностей существуют допустимые значения, которые приводят в инструкциях по подсчету запасов для каждого вида минерального сырья. Если относительная случайная погрешность окажется больше допустимой, то подсчет запасов будет ненадежным.

В табл.3.5 приведен пример обработки данных внутреннего контроля анализов. При расчетах следует обращать внимание на грубые (аномальные) различия между основными и контрольными измерениями, которые могут быть вызваны неслучайными причинами и классифицируются как промахи. Их присутствие может существенно исказить (увеличить) случайную погрешность.

Таблица 3.5