Расчет графика плотности вероятности нормального закона

Класс содержаний х, %	n		у	Произведения				t	f(t)	nт	Значения
				nу	nу2	nу3	nу4
30-32	2		-5	-10	50	-250	1250	-2,20	0,0355	2,1
32-34	6		-4	-24	96	-376	1504	-1,80	0,0790	4,6	0,252
34-36	9		-3	-27	81	-243	729	-1,41	0,1476	8,6	0,019
36-38	14		-2	-28	56	-112	224	-1,01	0,2396	13,9	0,001
38-40	20		-1	-20	20	-20	20	-0,62	0,3292	19,1	0,042
40-42	25		0	0	0	0	0	-0,22	0,3894	22,6	0,255
42-44	21		1	21	21	21	21	0,17	0,3932	22,8	0,142
44-46	17		2	34	68	136	272	0,57	0,3391	19,7	0,370
46-48	13		3	39	117	351	1053	0,96	0,2516	14,6	0,175
48-50	10		4	40	160	640	2560	1,38	0,1582	9,2	0,070
50-52	5		5	25	125	625	3125	1,75	0,0863	5,0	0,000
52-54	3		6	18	108	648	3880	2,15	0,0396	2,3	1,012
54-56	2		7	14	98	686	4802	2,55	0,0154	0,9
Сумма	147		–	82	1000	2106	19448	–	2,5037	145,4	2 = 2,338
Среднее	–		–	0,56	6,80	14,33	1323,3	–	–	–	–
Примечание. n – частота фактическая; у – условный номер класса; t – нормированные значения; f(t) – плотность вероятности; nт – частота теоретическая.

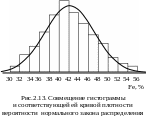
Сумма плотностей вероятности, равная 2,5037, близка к среднеквадратичному отклонению _у = 2,53. Если продолжить кривую плотности вероятности за пределы графика (рис.2.13), то сумма будет точно равна _у.

Чтобы перейти от плотности вероятности к теоретической частоте n_т, применяется формула

(2.36)

Здесь N = 147 (суммарное число измерений); h – размер (шаг) класса.

Поскольку в качестве аргумента взят номер класса у, шаг h = 1, _у = 2,53. Следовательно,

Такое же соотношение получится, если в качестве аргумента взять случайную величину х. Из табл.2.5 имеем h = 2,  = 5,06, и отношение h/ не изменится. Сумма теоретических частот 145,4 близка к общему числу значений N = 147. Продолжив кривую за пределы графика, можно убедиться, что суммы теоретических и фактических частот совпадут.

Сравнение фактических и теоретических частот в табл.2.13 показывает их сходство. Можно совместить частоты на одном графике, построив гистограмму по фактическим частотам n, а кривую плотности вероятности – по теоретическим частотам n_т (рис.2.13).

Последняя графа табл.2.13 позволяет рассчитать критерий ²:

(2.40)

где N_k – число классов сравнения частот.

Чтобы избежать грубых случайных расхождений, рекомендуется объединять соседние классы с малым числом фактических частот. В табл.2.13 объединены два первых и два последних класса. В результате число классов N_k = 11. Вычисленное значение ² = 2,338. Приняв вероятность  = 0,05 и зная число степеней свободы k = 11 – 3 = 8, из табл.2.11 найдем предельное значение = 15,51. Так как ² < , то следует признать, что с вероятностью p > (1 – ) = 0,95 распределение фактических частот не противоречит нормальному закону. Такая же проверка соответствия фактических частот теоретическим может быть выполнена для других законов распределения.

Возможен и другой способ проверки соответствия, но только нормальному закону. Он основан на том, что асимметрия и эксцесс нормального закона равны нулю. Оценивая степень отклонения фактических значений асимметрии и эксцесса от нуля с помощью какого-либо критерия, можно сделать заключение о соответствии или несоответствии распределения случайной величины нормальному закону. Обычно используется критерий распределения Стьюдента (см. табл.2.10), а при большом числе исходных данных – критерий нормального закона (см. табл.2.7). Проверяют две гипотезы: при числе степеней свободы k = n – 1 асимметрия А = 0 и эксцесс Е = 0. Согласно формуле (2.24) имеем

(2.41)

или проще , , где _А = , _Е = . Если t_A и t_Е будут меньше предельного значения t_пр, то распределение случайной величины не противоречит нормальному закону. Если t_A или t_Е больше предельного значения t_пр, то распределение противоречит нормальному закону. В качестве предельного значения можно брать t_пр = 3, что соответствует вероятности q = 0,997 (см. табл.2.6). Иногда вероятность принятия решения задается (например, q = 0,95), тогда t_пр определяют по табл.2.7 (t_пр = 1,96).

В рассматриваемом примере асимметрия и эксцесс рассчитаны по табл.2.5: А = 0,166; Е = –0,269 (см. пример 2.2). Вычислим _А = = 0,202; _Е =  = 0,404, тогда t_A = 0,166/0,202 = 0,82; t_Е = 0,269/0,404 = 0,67. При вероятности q = 0,95 имеем t_пр = 1,96. Так как t_A и t_Е меньше t_пр, то еще раз получаем подтверждение того, что распределение содержаний не противоречит нормальному закону.

Аналогичным способом можно проверить соответствие распределения случайной величины логнормальному распределению, оперируя с логарифмами значений случайной величины.

Критерии t_A и t_Е не требуют построения гистограммы, их удобно использовать при любом числе значений случайной величины, но область их применения ограничена нормальным и логнормальным законами. Критерий ² более универсален, его можно использовать для сравнения гистограмм с любыми законами распределения.

Возникает вопрос, с какой целью производится проверка гипотез о законах распределения. Ответ заключается в том, что при статистической обработке значений случайной величины нужно знать вероятность (т.е. надежность) принятия решений, а вероятность можно определить лишь тогда, когда известен закон распределения случайной величины.

2.2.8. Преобразование случайной величины

Большинство решений, принимаемых на базе статистических закономерностей, основано на нормальном законе распределения, играющем универсальную роль. Как было отмечено, при определенных условиях к нему приближаются логнормальный закон, распределение Стьюдента, распределение χ² и многие другие. Однако реальное распределение свойств геологических объектов часто отличается от нормального, что вызывает затруднения в принятии решений и в оценке достоверности получаемых выводов. Поэтому принятию решений обычно предшествует проверка соответствия распределения случайной величины нормальному закону, и, если соответствия нет, то можно попытаться преобразовать случайную величину, приведя ее распределение к нормальному. Подобное преобразование применялось выше, когда вместо случайной величины х вводилась новая случайная величина z = lnx. В результате асимметричное логнормальное распределение преобразовывалось в симметричное нормальное.

Представляют интерес такие преобразования, которые превращают произвольно распределенную случайную величину х в случайную величину z, распределение которой близко к нормальному. Задача заключается в подборе наилучшей функции преобразования.

Преобразование обычно меняет область существования случайной величины. Например, если случайная величина х меняется в пределах от нуля до +, то преобразованная случайная величина z = lnx имеет область существования от – до +. Поэтому учет области существования случайной величины может помочь в выборе наилучшего преобразования.

Если случайная величина x имеет область существования от a до b, то преобразование

(2.42)

меняет пределы ее существования от – до +, что во многих случаях эффективно. Частным случаем является ситуация, когда а = 0, b = 1 = 100 % (например, содержание химических элементов не может быть меньше нуля и больше 100 %), и формула преобразования имеет вид

. (2.43)

Если значения случайной величины х очень малы, то ею в знаменателе можно пренебречь, и получается формула z = lnx, лежащая в основе логнормального распределения. Наоборот, если значения х близки к единице, то получается формула преобразования в правоасимметричное логнормальное распределение z = –ln(1 – x).

Если случайная величина колеблется в пределах от –1 до +1 (например, коэффициент корреляции или многие тригонометрические функции), то эффективным является преобразование

(2.44)

или преобразование, предложенное Фишером

(2.45)

Для преобразования могут быть использованы также степенные функции вида z = x^a или z = x^–a, где а может принимать значения от 1/2 до 3 [2].

Пример 2.5. Рассмотрим подбор функции преобразования для случайной величины х с асимметричным распределением (табл.2.14).

Таблица 2.14