Коэффициенты вероятности распределения 2 при заданных вероятности и числе степеней свободы k
k |
Вероятность |
k |
Вероятность |
||||||||
0,10 |
0,05 |
0,025 |
0,01 |
0,005 |
0,10 |
0,05 |
0,025 |
0,01 |
0,005 |
||
1 |
2,71 |
3,84 |
5,02 |
6,64 |
7,88 |
16 |
23,54 |
26,30 |
28,84 |
32,00 |
34,27 |
2 |
4,60 |
5,99 |
7,38 |
9,21 |
10,66 |
17 |
24,77 |
27,59 |
30,19 |
33,41 |
35,72 |
3 |
6,25 |
7,82 |
9,35 |
11,34 |
12,54 |
18 |
25,99 |
28,87 |
31,53 |
34,80 |
37,16 |
4 |
7,78 |
9,49 |
11,14 |
13,28 |
14,86 |
19 |
27,20 |
30,14 |
32,85 |
36,19 |
38,58 |
5 |
9,24 |
11,07 |
12,83 |
15,09 |
16,75 |
20 |
28,41 |
31,41 |
34,17 |
37,57 |
40,00 |
6 |
10,64 |
12,59 |
14,45 |
16,81 |
18,55 |
21 |
29,62 |
32,67 |
35,48 |
38,93 |
41,40 |
7 |
12,02 |
14,07 |
16,01 |
18,48 |
20,28 |
22 |
30,81 |
33,92 |
36,78 |
40,29 |
42,80 |
8 |
13,36 |
15,51 |
17,54 |
20,09 |
21,96 |
23 |
32,01 |
35,16 |
38,08 |
41,64 |
44,18 |
9 |
14,68 |
16,92 |
19,02 |
21,67 |
23,59 |
24 |
33,20 |
36,42 |
39,36 |
42,98 |
45,56 |
10 |
15,99 |
18,31 |
20,48 |
23,21 |
25,19 |
25 |
34,38 |
37,65 |
40,65 |
44,31 |
46,93 |
11 |
17,28 |
19,68 |
21,92 |
24,72 |
26,76 |
26 |
35,56 |
38,88 |
41,92 |
45,64 |
46,29 |
12 |
18,55 |
21,03 |
23,34 |
26,22 |
28,30 |
27 |
36,74 |
40,11 |
43,19 |
46,96 |
49,64 |
13 |
19,81 |
22,36 |
24,74 |
27,69 |
29,82 |
28 |
37,92 |
41,34 |
44,46 |
48,28 |
50,99 |
14 |
21,06 |
23,68 |
26,12 |
29,14 |
31,32 |
29 |
39,09 |
42,56 |
45,72 |
49,59 |
52,34 |
15 |
22,31 |
25,00 |
27,49 |
30,58 |
32,80 |
30 |
40,26 |
43,77 |
46,98 |
50,89 |
53,67 |
Пример 2.3. Выбрана вероятность = 0,05, число степеней свободы k = 15. Необходимо найти 2.
Из табл.2.11 получаем 2 = 25,0. Если число степеней свободы большое (например, k = 50), а вероятность та же, то воспользуемся табл.2.6 нормального закона, для чего найдем Ф(t) = 1 – 2 = 0,90, ей соответствует найденное интерполяцией значение t = 1,645. Из формулы (2.35) следует, что 2 = 66,45. Для сравнения точное значение 2 = 67,50.
2.2.6. Распределение Фишера
Распределение
Фишера, называемое также
F-распределением, используется для
проверки гипотезы о равенстве дисперсий
случайных величин. В качестве критерия
служит отношение несмещенных оценок
дисперсий F =
,
причем в числитель отношения всегда
помещают бόльшую дисперсию, т.е.
>
.
Плотность вероятности распределения
величины F выражается формулой
,
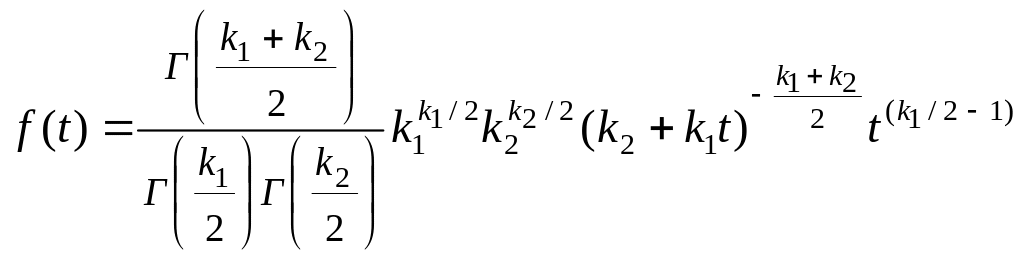(2.37)
График плотности вероятности асимметричен (рис.2.12) и имеет максимум (моду)
.
(2.38)
Практическое значение имеет зависимость коэффициента t (критерия) от вероятности (ей соответствует заштрихованная площадь на рис.2.12) при заданных степенях свободы k1 и k2. Оценивается вероятность того, что отношение превысит некоторое критическое значение t. Если отношение больше t, то дисперсии различаются между собой с вероятностью p = 1 – .
Таблица 2.12
Коэффициенты вероятности F-распределения при = 0,05 = 5 %
k2 |
Число степеней свободы k1 |
||||||||||||||
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
30 |
40 |
60 |
120 |
|
|
3 |
9,28 |
9,12 |
9,01 |
8,94 |
8,89 |
8,85 |
8,81 |
8,79 |
8,70 |
8,66 |
8,62 |
8,59 |
8,57 |
8,55 |
8,53 |
4 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
6,00 |
5,96 |
5,86 |
5,80 |
5,75 |
5,72 |
5,69 |
5,66 |
5,63 |
5 |
5,41 |
5,19 |
5,05 |
4,95 |
4,88 |
4,82 |
4,77 |
4,74 |
4,62 |
4,56 |
4,50 |
4,46 |
4,43 |
4,40 |
4,36 |
6 |
4,76 |
4,53 |
4,39 |
4,28 |
4,21 |
4,15 |
4,10 |
4,06 |
3,94 |
3,87 |
3,81 |
3,77 |
3,74 |
3,70 |
3,67 |
7 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
3,68 |
3,64 |
3,51 |
3,44 |
3,38 |
3,34 |
3,30 |
3,27 |
3,23 |
8 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
3,39 |
3,35 |
3,22 |
3,15 |
3,08 |
3,04 |
3,01 |
2,97 |
2,93 |
9 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
3,18 |
3,14 |
3,01 |
2,94 |
2,86 |
2,83 |
2,79 |
2,75 |
2,71 |
10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
3,02 |
2,98 |
2,85 |
2,77 |
2,70 |
2,66 |
2,62 |
2,58 |
2,54 |
15 |
3,29 |
3,06 |
2,90 |
2,79 |
2,71 |
2,64 |
2,59 |
2,54 |
2,40 |
2,33 |
2,25 |
2,20 |
2,16 |
2,11 |
2,07 |
20 |
3,10 |
2,87 |
2,71 |
2,60 |
2,51 |
2,45 |
2,39 |
2,35 |
2,20 |
2,12 |
2,04 |
1,99 |
1,95 |
1,90 |
1,84 |
30 |
2,92 |
2,69 |
2,53 |
2,42 |
2,33 |
2,27 |
2,21 |
2,16 |
2,01 |
1,93 |
1,84 |
1,79 |
1,74 |
1,68 |
1,62 |
40 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
2,12 |
2,08 |
1,92 |
1,84 |
1,74 |
1,69 |
164 |
1,58 |
1,51 |
60 |
2,76 |
2,63 |
2,37 |
2,25 |
2,17 |
2,10 |
2,04 |
1,99 |
1,84 |
1,75 |
1,65 |
1,59 |
1,53 |
1,47 |
1,39 |
120 |
2,68 |
2,45 |
2,29 |
2,18 |
2,09 |
2,02 |
1,96 |
1,91 |
1,75 |
1,66 |
1,55 |
1,50 |
1,43 |
1,35 |
1,25 |
|
2,60 |
2,37 |
2,21 |
2,10 |
2,01 |
1,94 |
1,88 |
1,83 |
1,67 |
1,57 |
1,46 |
1,39 |
1,32 |
1,22 |
1,00 |
Коэффициент t зависит от трех величин: вероятности , степеней свободы k1 и k2, что трудно отобразить в одной таблице, поэтому применяется серия таблиц с различными значениями вероятности . В качестве примера приведена табл.2.12 значений коэффициента t при наиболее часто используемой вероятности = 0,05.
Пример 2.4.
Необходимо сравнить две дисперсии:
=
= 5,22 и
= 1,86.
Число измерений соответственно n1 = 16,
n2 = 31.
Находим отношение F = 5,22/1,86 = 2,81, степени свободы k1 = 16 – 1 = 15, k2 = 31 – 1 = 30. Из табл.2.12 имеем t = 2,01. Поскольку значение F = 2,81 больше критерия t = 2,01, дисперсии и различаются между собой с вероятностью более p = 1 – 0,05 = = 0,95.
2.2.7. Построение графика плотности вероятности,
проверка гипотезы о законе распределения
Во многих случаях желательно построить график кривой плотности вероятности того или иного закона распределения и совместить его с гистограммой, что позволяет наглядно оценить степень их сходства. В процессе расчета точек кривой можно получить количественные меры соответствия фактической гистограммы теоретическому закону распределения случайной величины.
Рассмотрим
построение кривой плотности вероятности
нормального закона на примере данных
табл.2.4 и рис.2.1. Чтобы построить кривую,
необходимо рассчитать значения функции
f(t) по
формуле (2.22) и нанести их на график. Имеет
смысл рассчитать лишь те значения,
которые соответствуют серединам классов
гистограммы. Расчет выполнен по форме
табл.2.13, в которой первые
семь граф заимствованы из табл.2.5. Они
нужны для расчета статистических
характеристик. Для построения кривой
достаточно иметь две характеристики:
среднее значение и дисперсию. В качестве
аргумента можно брать номера классов
у, что значительно упрощает расчеты.
В результате вычислений получены
= 6,40;
у = 2,53.
Далее по формуле (2.24) нужно перейти от
условной величины у к нормированной
величине t:
.
Зная t, можно рассчитать плотность вероятности f(t) либо по табл.2.6, либо по формуле (2.22). Все необходимые расчеты выполнены в табл.2.13.
Таблица 2.13