Питання для самоконтролю

1. Яка функція називається важкооборотною?

2. Що таке важкооборотна функція з секретом?

3. Дайте означення ядра функції.

4. Викладіть загальний вид алгоритму імовірнісного шифрування.

5. Яким чином застосовуються односторонні функції для побудови класичних асиметричних криптосистем?

Задачі до §12

1. Довести, що функція Рабіна є бієкцією на , а функція RSA – бієкцією на .

2. Довести, що при кількість парних квадратичних лишків у дорівнює кількості непарних.

3. Виходячи з припущення, що не існує поліноміального алгоритму розпізнавання квадратичних лишків в , довести, що предикат парності є ядром для функції Рабіна.

4. Чи є предикат парності ядром функції дискретного піднесення до степеня? Чому?

5. Нехай RSA-функція. Позначимо , 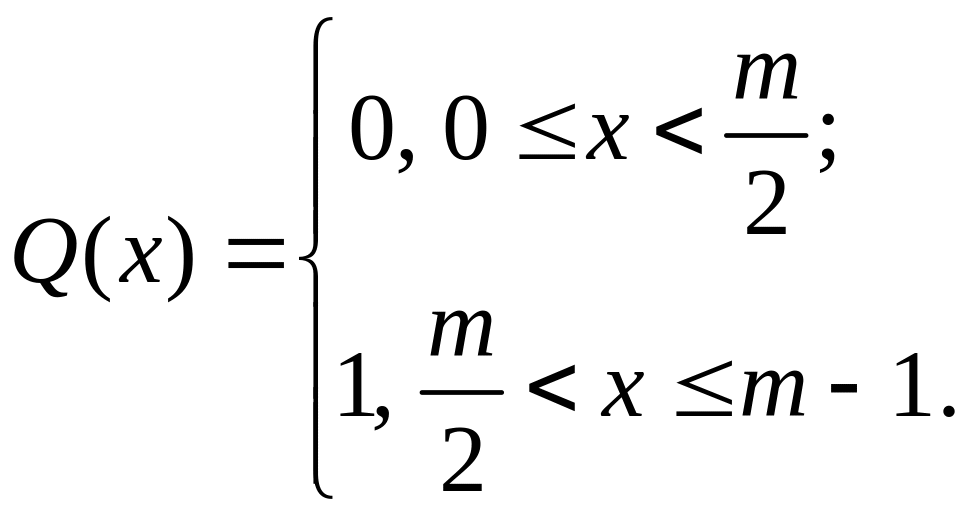Довести, що задачі обчислення предикатів , поліноміально еквівалентні.

7. Для кожного асиметричного алгоритму, наведеного у параграфі, визначити, якими алгоритмами та за який час виконуються окремі кроки. Чи будуть алгоритми поліноміальними?

8. Переконатись, що при коректному виконанні протоколу Діффі-Хеллмана абоненти в результаті виконання перетворень (12.1) і (12.2) дійсно встановлять спільний ключ.

9. Переконатись, що в результаті перетворень (12.3) та (12.4) дійсно отримаємо відкритий текст М.

10. Переконатись, що алгоритми перевірки цифрового підпису є коректними.

11. Переконатись, що протоколи доведення без розголошення мають властивість повноти.

Література

1. Кострикин А. И. Введение в алгебру. Основы алгебры. – М.: Наука, 1994. – 307 с.

2. Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. / Пер. с англ. – М.: Мир, 1988. – 822 с.

3. Коблиц Н. Курс теории чисел и криптографии. / Пер. с англ. – М.: Научное изд-во ТВП, 2001. – 254 с.

4. Ван дер Варден Б. Л. Алгебра. / Пер. с англ. – М.: Наука, 1979. – 649 с.

5. Вербицький О. В. Вступ до криптології. – Львів: Видавництво науково-технічної літератури, 1998. – 247 с.

6. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. / Пер. с англ. – М.: Мир. 1979. – 534 с.

7. Гэри М, Джонсон Д. Вычислительные машины и труднорешаемые задачи. / Пер. с англ. – М.: Мир, 1982. – 416 с.

8. Ван Тилборг Х.К.А. Основы криптологии. / Пер. с англ. – М.: Мир, 2006. – 471 с.

9. Математические компьютерные основы криптологии: Учеб. пособие / Ю.С. Харин, В.И. Берник, Г.В. Матвеев, С.В. Агиевич – Мн.: Новое знание, 2003. – 382 с.

10. Шнайер Б. Прикладная криптография. / Пер. с англ. – М.: Триумф, 2003. – 815 с.

Предметний покажчик

s-гладке число, 142

автоморфізм внутрішній, 24

груп, 30

кілець, 46

адитивна група кільця, 38

алгебраїчна система, 8

алгоритм експоненційний, 91

поліноміальний, 91

субекспоненційний, 92

алгоритм з Оракулом, 105

розпізнвання мови з односторонньою помилкою, 103

алфавіт, 89

асоційовані елементи, 55

Блюма криптосистема, 152

Блюма прості, 118

випадкова послідовність, 101

Вільсона теорема, 36

Гауса квадратичний закон взаємності, 116

гомоморфізм груп, 24

кілець, 46

Горнера схема, 97

група, 9

абелева, 9

лишків, 11

породжена елементом, 14

скінчена, 12

циклічна, 14

дискретний логарифм, 141

дільник нуля, 39

лівий, 39

правий, 39

елемента, 54

лівий, 54

правий, 54

Діффі-Хеллмана протокол відкритого обміну ключами, 153

доведення без розголошення, 161

довжина входу алгоритму, 89

додатковий вхід алгоритму, 101

Евкліда алгоритм, 63

розширений, 64

елемент нейтральний, 9

нульовий групи, 9

кільця, 38

обернений, 9

оборотний, 20

одиничний, 9

кільця, 39

елемент породжуючий, 14

протилежний, 10

нескінченного порядку, 13

скінченного порядку, 13

твірний, 14

утворюючий, 14

кільця асоційований з елементом, 55

оборотний, 54

простий, 55

ендоморфізм груп, 24

кілець, 46

епіморфізм груп, 24

кілець, 46

Ератосфена решето , 128

задача дискретного логарифмування, 141

про розподіл таємниці, 79

розпізнавання мови, 102

ідеал кільця, 42

головний, 43

максимальний, 55

найменший (мінімальний), що містить даний елемент, 42

породжений елементом, 43

простий, 55

ізоморфізм груп, 24

кілець, 46

імовірнісний алгоритм, 101

розподіл, 100

імовірність події, 100

помилки алгоритму, 101

індекс підгрупи, 17

квадратний корінь за модулем, 111

квадратичний лишок, 111

нелишок, 111

Китайська теорема про лишки, 72

узагальнена, 78

кільце, 38

без дільників нуля, 40

головних ідеалів, 43

з одиницею, 39

комутативне, 39

лишків, 70

скінчене, 42

цілісне, 40

клас лишків за ідеалом, 44

спряженості, 31

суміжності лівий, 16

правий, 16

конгруентність за модулем ідеалу, 44

конгруенція, 69

Лас-Вегас алгоритм, 102

Лагранжа теорема, 18

Лежандра символ, 112

літера, 90

Мерсена число, 88

метод числового решета, 130

Міллера-Рабіна тест, 136

моноїд, 8

Монте-Карло алгоритм, 102

мультиплікативна група кільця, 55

лишків, 70

найбільший спільний дільник (НСД), 63

найменше спільне кратне (НСК), 63

напівгрупа, 8

нормалізатор множини, 31

нормальний дільник, 25

носій операції, 8

образ гомоморфізму, 25

Ойлера критерій, 113

теорема, 72

узагальнена, 81

функція, 22, 71

узагальнена, 81

операція асоціативна, 8

бінарна, 8

комутативна, 8

Оракул, 105

Підгрупа, 13

власна, 13

породжена елементом, 13

тривіальна, 13

нормальна, 25, 26

підкільце, 42

подія, 100

елементарна, 100

неможлива, 100

поле, 40

поліноміально еквівалентні задачі, 106

порівняння, 69

порядок групи, 12

елемента, 13

кільця, 42

предикат важкооборотної функції, 149, 151

з секретом, 151

представник класу суміжності, 16

простір подій, 100

псевдоквадрат, 118

псевдопросте число Ферма, 131

Ойлера, 132

рівняння класів спряженості , 33

різниця елементів групи ліва, 15

права, 15

розв’язок системи порівнянь, 72

частковий, 73

канонічний, 73

загальний, 73

канонічний, 73

Сільвера-Поліга-Хеллмана метод, 142

сильно псевдопросте число, 133

символ, 89

система представників класів суміжності, 28

шифрування RS, 155

Ель-Гамаля, 156

цифрового підпису DS, 160

RS, 157

Ель-Гамаля, 158

Шнорра, 159

слово, 89

Соловея-Штрассена тест, 135

спряжені елементи, 31

таблиця Келі, 12

теорема про структуру мультиплікативної групи кільця лишків, 71

факторгрупа, 28

факторкільце, 45

Ферма мала теорема, 36, 72

число, 66

фундаментальна теорема арифметики, 67

функція важкооборотна, 147, 148

одностороння, 147

з секретом, 149

характеристика кільця, 51

центр групи, 32

час роботи алгоритму, 90

число Кармайкла, 131

просте, 62

складене , 62

ядро важкооборотної функції, 149, 150

гомоморфізму, 25

Якобі символ, 114

180