5.2. Розклад на прості множники. Фундаментальна теорема арифметики

Яскравим прикладом застосування наслідків з алгоритму Евкліда є наступна теорема.

Теорема 5.15 (фундаментальна теорема арифметики): будь-яке натуральне число, більше за 1, однозначно (з точністю до порядку співмножників) розкладається на прості натуральні множники.

Доведення: по-перше, необхідно показати, що такий скінченний розклад на прості множники існує. Доведення виконується методом математичної індукції. Нехай розклад на прості множники існує для всіх чисел, не більших за п (п – будь-яке фіксоване натуральне число, не менше за 2). Покажемо, що розклад існує і для числа п + 1. Можливими є два випадки:

n + 1 – просте число; тоді для нього твердження теореми виконується;

n + 1 – складене; тоді аN: 1  а  п, а|(п + 1) і, відповідно, п + 1 = ab, 1  b  п; за припущенням індукції, кожне з чисел a та b або просте, або розкладається на прості множники; отже, число n + 1 також розкладається на прості множники.

По-друге, необхідно показати, що розклад на прості множники є однозначним. Нехай існує два різних розклади числа a. Допускаючи використання показника степеню, рівного нулю, можемо вважати, що обидва розклади складаються з однакових множників.

Нехай a =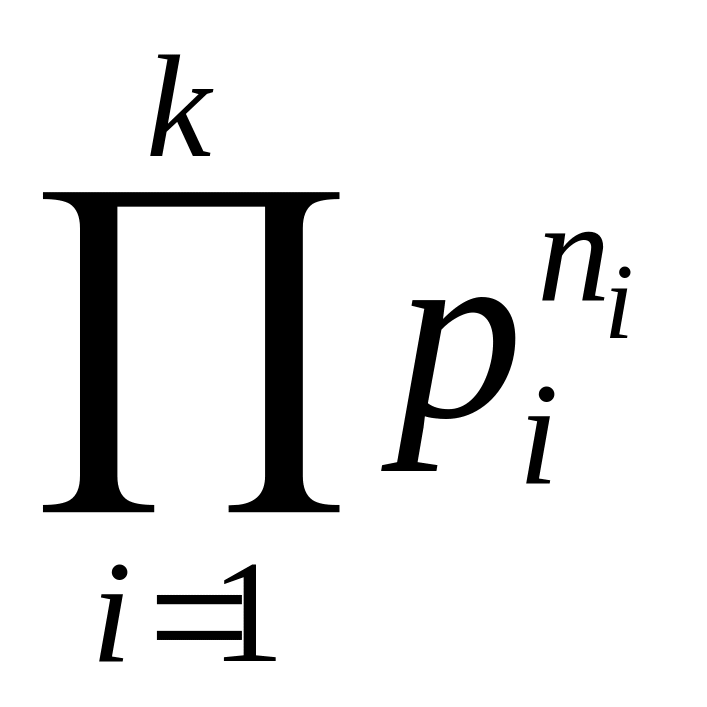 = 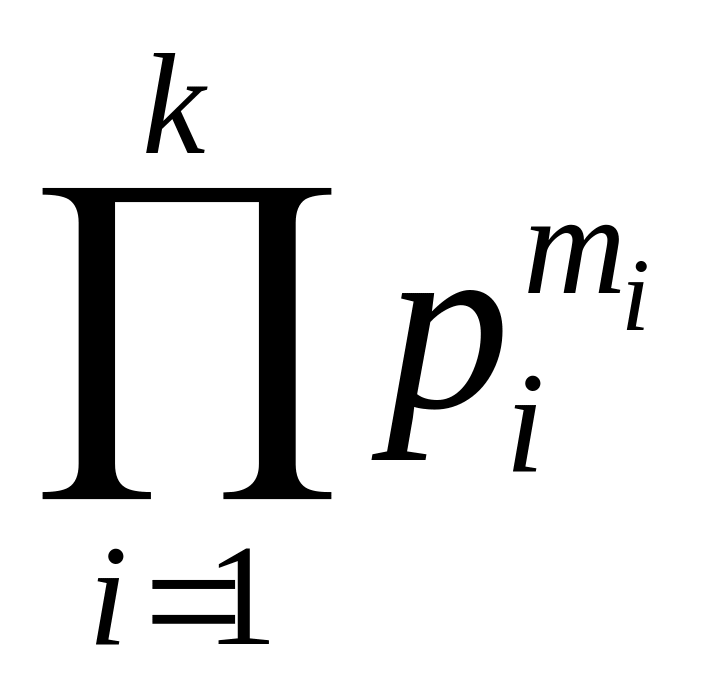, , причому при . Оскільки p_i, – прості, то з виразу випливає . Однозначність розкладу будемо доводити від супротивного: нехай i: n_i  m_i. Для визначеності вважаємо, що n_i > m_i; розділимо ліву і праву частини на . Тоді ліва частина ділиться на p_i (навіть на ), отже, права частина теж ділиться на p_i. Тоді за узагальненням наслідку 5.13 алгоритму Евкліда один з множників у правій частині ділиться на p_i, що призводить до суперечності з тим, що при . Теорему доведено.

Зауваження 5.16: теорема залишається справедливою і для цілих чисел, але в цьому випадку під однозначністю розкладу слід розуміти однозначність з точністю до порядку і асоційованості.

Означення 5.17: канонічним розкладом цілого числа п називається представлення п у вигляді

,

де , і ₁, ₂, …_sÎN.

5.3. Конгруенції (порівняння) та їх властивості

Означення 5.18: будемо говорити, що число xZ конгруентне числу yZ за модулем nÎN, і записувати x  y (mod n), якщо x mod n = y mod n (тобто х та у при діленні на п мають однакові залишки).

Вираз x  y (mod n) називається конгруенцією або порівнянням.

Зауваження 5.19: вираз "x mod n = y mod n" рівносильний виразу "x – y n", а також висловлюванням "елементи x та y кільця Z конгруентні за модулем ідеалу, породженого елементом n" та " " (доведіть самостійно). Тому означення 5.18 може бути сформульовано принаймні трьома способами.

Твердження 5.20 (властивості конгруенцій).

1. Відношення конгруентності є відношенням еквівалентності (тобто є відношенням рефлективності, симетричності та транзитивності).

2. Нехай x₁  y₁ (mod n), x₂  y₂ (mod n). Тоді x₁ + x₂  y₁ + y₂ (mod n), x₁ - x₂  y₁ - y₂ (mod n) і x₁·x₂  y₁·y₂ (mod n).

3. Нехай x  y (mod n), d|x, d|y, (d, n) = 1. Тоді ).

4. Нехай x  y (mod n), d|x, d|y, d|n. Тоді .

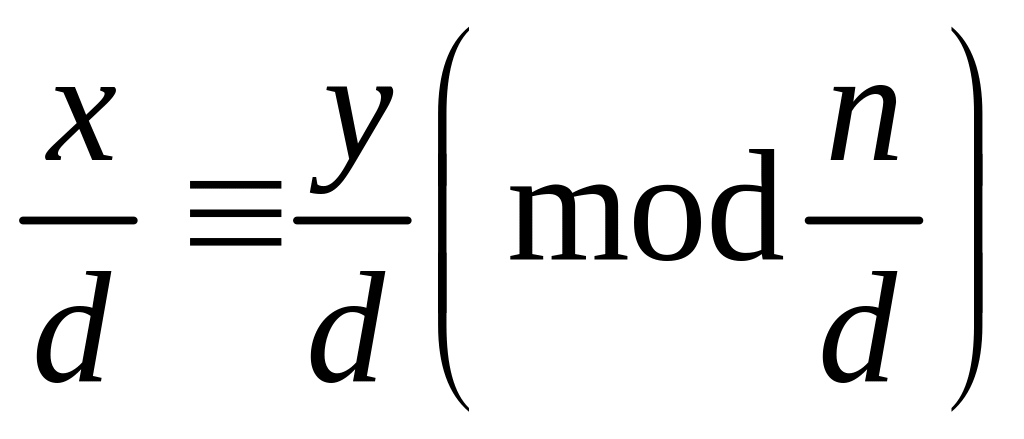5. Нехай x  y (mod n), m|n. Тоді x  y (mod m).

6. Нехай (m, n) = 1. Тоді

x  y (mod m n)  (x  y (mod m))(x  y (mod n)).

Доведення: пункти 1 та 2 доводяться безпосередньою перевіркою.

Для доведення пункту 3 необхідно показати, що n| .

Оскільки n|(x – y) = , (d, n) = 1, то за наслідком 5.12 алгоритму Евкліда n| .

За умовою пункту 4, = , отже п. 4 виконується.

Доведення пункту 5 є тривіальним.

З лівої частини рівносильності в пункті 6 випливає права за пунктом 5. Доведемо зворотне твердження. За умовою, т|(x – y), п|(x – y), та (т,п)=1. Тоді за наслідком 5.14 алгоритму Евкліда тп|(x – y), тобто x  y (mod m n). Твердження доведено.

Приклад 5.21: використовуючи конгруенцію, покажемо, що 11 ділить 73524.

Оскільки 10  –1 (mod 11), то за властивостями конгруенцій:

100  10² (mod 11)  (–1)² (mod 11) º 1 (mod 11);

1000  –1 (mod 11);

10000  1 (mod 11).

Тому 73524 mod 11 = (7·10000 + 3·1000 + 5·100 + 2·10 + 4) mod 11= =(7 – 3 + 5 – 2 + 4) mod 11 = 11 mod 11= 0 mod 11.