§5. Алгоритм Евкліда. Основна теорема арифметики. Конгруенції та їх властивості. Китайська теорема про лишки

5.1. Прості числа, нсд, нск. Розширений алгоритм Евкліда, його наслідки

Протягом даного параграфу та деяких наступних будемо працювати з цілими та натуральними числами.

Означення 5.1: число рÎZ, р ≠ 1, називається простим, якщо воно не має натуральних дільників, відмінних від 1 і р.

В протилежному випадку число називається складеним.

Як було зазначено раніше, прості числа – це прості елементи кільця цілих чисел. Число 1 не відноситься ні до простих, ні до складених чисел – це оборотний елемент кільця цілих чисел. У нього є лише один натуральний дільник.

З курсу шкільної алгебри відоме наступне твердження.

Твердження 5.2: aZ, bN !(q, r), 0  r < b, q, rZ:

a = bq + r, (5.1)

де q – частка від ділення a на b, r – залишок від (цілочисельного) ділення a на b (тобто ).

Зауваження 5.3: обмеження bN замість bZ вводиться лише для того, щоб залишок r був визначений однозначно.

В §1 для позначення залишку від ділення a на b було введено позначення: r = a mod b. Якщо r = 0, то будемо говорити, що "a ділиться на b; b ділить a; b дільник a; a кратне b" і позначати або .

Означення 5.4: найбільшим спільним дільником (НСД) чисел a і b називається таке число dN, що має наступні властивості:

1) d|a, d|b;

2) c ≠ d: (c|a, c|b)  c < d.

Найбільший спільний дільник чисел і a і b позначається НСД(a, b) або (a, b).

Означення 5.5: найменшим спільним кратним (НСК) чисел a і b називається таке k N, що:

1) a|k, b|k

2) l ≠ k : (a|l, b|l)  l > k.

Найменше спільне кратне чисел і a і b позначається НСК(a, b).

Зауваження 5.6: пункти 2) у означеннях 1 і 2 можна замінити, відповідно, наступними:

2*) c ≠ d: (c|a, c|b)  c|d;

2**) l ≠ k : (a|l, b|l)  k|l.

У даному випадку при заміні обидва означення не зміняться, але, як ми побачимо далі, пункти 2*) і 2**) є більш загальними і можуть бути застосовані для довільного (у т.ч. неупорядкованого) кільця, а не тільки для кільця цілих чисел.

Для знаходження НСД(a, b) використовується алгоритм Евкліда. Він базується на двох очевидних співвідношеннях:

(a, b) = (a, b mod a) (при a  b), (5.2)

(a, 0) = a, (5.3)

які є наслідками твердження 5.2.

Приклад 5.7: знаходження НСД(17, 12) та НСД(8,12) за алгоритмом Евкліда.

(12, 17) = (12, 5) = (5, 2) = (2, 1) = (1, 0) = 1;

(81, 12) = (12, 9) = (9,3) = (3,0) = 3.

Далі ми розглянемо так званий розширений алгоритм Евкліда, який не тільки знаходить НСД двох чисел a, bÎZ, але й його подання у вигляді їх цілочисельної лінійної комбінації, а також дозволяє доводити багато корисних властивостей кільця цілих чисел.

Покажемо, як працює розширений алгоритм Евкліда для знаходження (a, b) та його подання у вигляді лінійної комбінації чисел a, bÎZ, a > b, b ≠ 0. В загальному випадку він складається з наступних кроків.

Розширений алгоритм Евкліда

Позначимо r₀ =a, r₁ = b.

На кожному кроці будемо знаходити лишок від ділення та подавати ділене у вигляді (5.1):

1 крок: r₂ = r₀ mod r₁, (r₀ = q₁r₁ + r₂),

2 крок: r₃ = r₁ mod r₂, (r₁ = q₂r₂ + r₃),

3 крок: r₄ = r₂ mod r₃, (r₂ = q₃r₃ + r₄),

…………………………………..

і-ий крок: r_i = r_i–2 mod r_i–1, (r_і–2 = q_і–1r_і–1 + r_і)

…………………………………..

m-ий крок: r_m+1 = r_m–1 mod r_m = 0.

Якщо r_m+1 = 0, то (a, b) = r_m.

Покажемо коректність роботи алгоритму (тобто те, що алгоритм закінчить роботу та видасть вірний результат). Оскільки r_i < r_i–1, то алгоритм закінчить роботу не більше, ніж за b кроків (випливає з (5.3)). З (5.2) випливає, що алгоритм видасть вірний результат (доводиться методом математичної індукції за i).

Ефективність роботи алгоритму. Зрозуміло, що кількість кроків m  b (оскільки 0  r_i  r_i–1). Але ця оцінка є грубою, її можна суттєво покращити. Для цього доведемо, що r_i+1 < 1/2·r_i–1. Дійсно, можливі два випадки: або r_i < 1/2·r_i–1, тоді r_i+1 < r_i < 1/2·r_i–1, або r_i > 1/2·r_i–1, тоді r_i+1 = r_i–1 mod r_i = r_i–1 – r_i < 1/2·r_i–1, тобто у будь-якому випадку оцінка r_i+1 < 1/2·r_i–1 є вірною.

З отриманої оцінки випливає, що за кожні два кроки алгоритму величина r_i зменшується не менш, ніж в 2 рази, отже, бітова довжина числа r_i за кожні два кроки алгоритму зменшується як мінімум на один біт. Тому потрібно не більше за 2log₂(b + 1) кроків для завершення роботи алгоритму.

Розглянемо основні наслідки з розширеного алгоритму Евкліда.

Наслідок 5.8: якщо d = (a, b), то u, vZ: d = au + bv.

Доведення: нехай d = (a, b). Якщо алгоритм закінчив роботу на кроці m, то r_m+1 = 0, r_m = d. Проте r_m = r_m–2 mod r_m–1, звідки r_m–2 = q_m–1r_m–1 + r_m і d = r_m–2 – q_m–1r_m–1, тобто d = (r_m–1, r_m–2), де (х, у) – деяка лінійна функція від х, у з цілими коефіцієнтами. Але r_m–1, r_m–2 також є лінійними функціями з цілими коефіцієнтами від попередніх r_і, і < m – 2. Зазначимо, що суперпозиція таких лінійних функцій теж є лінійною з цілими коефіцієнтами. Таким чином, рухаючись "знизу вгору" за кроками алгоритму, представимо d як цілочисельну лінійну комбінацію чисел a та b.

Наслідок 5.9: якщо (a, b) =1, то u, vZ: au + bv = 1.

Даний наслідок є частковим випадком попереднього, але він дуже часто застосовується при доведенні різних тверджень та розв’язуванні задач у теорії чисел, тому ми виділяємо його окремо.

Приклад 5.10:

Нехай a = 17, b = 12. Тоді (12, 17) = (12, 5) = (5, 2) = (2, 1) = (1, 0) = 1.

За розширеним алгоритмом Евкліда:

17 = 12 + 5  5 = 17 – 12,

12 = 2·5 + 2  2 = 12 – 5·2,

5 = 2·2 + 1  1 = 5 – 2·2,

2 = 2·1.

Підставляючи у передостанню рівність замість числа 2 його вираз з другої рівності, зводячи "подібні" доданки та потім підставляючи замість числа 5 його вираз з першої рівності, отримаємо:

1 = 5 – 2·2 = 5 – 2(12 – 5·2) = 5·5 – 2·12 = 5(17 – 12) – 2·12 = 5·17 – 7·12.

Отже, у даному випадку ми знайшли цілі коефіцієнти u = –7 та v = 5.

Твердження 5.11 (узагальнення наслідку 5.8 з алгоритму Евкліда): нехай

d = (m₁, …, m_r), m₁, …, m_rZ.

Тоді

u₁, …, u_rZ: .

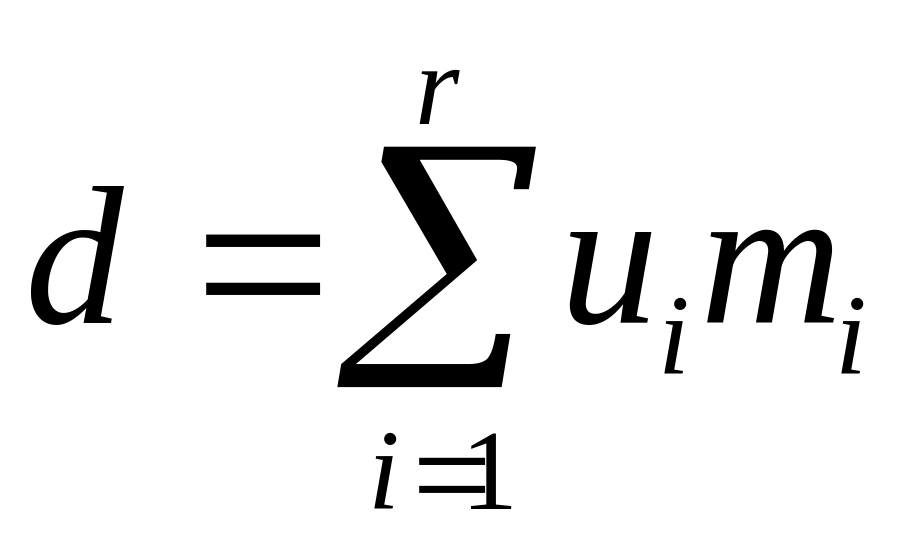Доведення: доведемо твердження для r = 3 (для r > 3 доведення проводиться аналогічно).

Нехай (m₁, m₂) = d₁₂, тоді d = (m₁, m₂, m₃) = (d₁₂, m₃), отже, d = vd₁₂ + + um₃ = v(u₁₁m₁ + u₁₂m₂) + um₃  d = u₁m₁ + u₂m₂ + u₃m₃. Доведення закінчено.

Наслідок 5.12: нехай а, b, cZ, c|ab та (с, a) = 1. Тоді c|b.

Доведення: за наслідком 5.9, u, vZ: au + сv = 1. Домножимо обидві частини рівності на b: aub + сvb = b. За умовою, перший доданок у лівій частині рівності ділиться на с, другий – також, тому ліва частина рівності ділиться на с, отже b також ділиться на с.

Наслідок 5.13: нехай р – просте число. Тоді: р|ab  p|a або p|b.

Доведення: нехай р|ab і p не ділить a, тоді (p, a) = 1, і за наслідком 3 отримаємо p|b.

Наслідок 5.13 можна узагальнити: якщо добуток довільної кількості цілих чисел ділиться на просте число, то принаймні один з його множників ділиться на це число.

Наслідок 5.14: нехай a|c, b|c i (a, b) = 1. Тоді ab|c.

Доведення: за наслідком 5.9, u, vZ: au + bv = 1. Домножимо обидві частини рівності на с: auс + bvс = с. Оскільки b|c, то ab ділить перший доданок у лівій частині рівності; аналогічно, ab ділить другий доданок у лівій частині рівності. Отже, ab ділить ліву частину рівності, тому ab|c.