
- •1050002 «Администрирование информационных систем»
- •История открытия фуллерена.
- •Структурные свойства фуллерена.
- •Синтез фуллерена.
- •Сверхпроводящие соединения с с60
- •Влияние малых добавок фуллереновой сажи на антифрикционные и противоизносные свойства птфэ
- •Другие области применения фуллеренов.
- •Однослойная и многослойная углеродные нанотрубки. Получение углеродных нанотрубок.
- •5. Исследование процесса механоактивации смесей порошка меди с унс
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых»
(ВлГУ)
Институт прикладной математики и информатики, био- и нанотехнологий
Факультет прикладной математики и физики
Кафедра «Основы нанотехнологий и теоретическая физика»
Рау В. Г., Ваганов В. Е.
ОСНОВЫ НАНОТЕХНОЛОГИЙ
Курс лекций
по дисциплине «Основы нанотехнологий» для студентов ВлГУ,
обучающихся по направлениям: 103000, «Информационные технологии»,
1050002 «Администрирование информационных систем»
Владимир – 2013
ОГ Л А В Л Е Н И Е
Стр
ЛЕКЦИЯ 1. Введение в курс дисциплины «Основы нанотехнологий»
Масштабная шкала. ……………..………………………………………. ………… 3
ЛЕКЦИЯ 2. Структура и свойства вещества. Атомно-молекулярная структура вещества. Электроны. Зонная теория. Деление веществ на проводники, диэлектрики и полупроводники. Размерные эффекты. Нанокластеры. ……………………….. 12
ЛЕКЦИЯ 3. Электромагнитные основы нанотехнологии. Законы электродинамики. Электромагнитные волны. Фотонные кристаллы и голография……………. 20
ЛЕКЦИЯ 4. Методы исследования нанообъектов. Масс-спектроскопия. Растровый электронный микроскоп. Атомно-силовой микроскоп. Рентгеновские
дифрактометры. Туннельный микроскоп.…………. .. ………………… 28
ЛЕКЦИЯ 5. Нанообъекты. Пути создания нанообъектов.
Самоорганизация нанообъектов: «снизу-вверх». Наноструктурный анализ
по дифракционным данным. …………………………….……… ……… 35
ЛЕКЦИЯ 6. Нанообъекты. Пути создания нанообъектов.
Внешнее воздействие: «сверху-вниз»). Фуллерены. …………………………… 45
ЛЕКЦИЯ 7. Нанообъекты. Пути создания нанообъектов. Внешнее
воздействие: «сверху-вниз»). Графен. …………………………… 49
ЛЕКЦИЯ 8. Нанообъекты. Пути создания нанообъектов. Внешнее
воздействие: «сверху-вниз»). Углеродные нанотрубки………………………… 53
ЛЕКЦИЯ 9. Нанообъекты. Пути создания нанообъектов. Внешнее
воздействие: «сверху-вниз»). Нанополимеры (некоторые перспективы)……… 62
ЛИТЕРАТУРА. ………………………………………………………………………. 68
ВВЕДЕНИЕ. Курс лекций базируется не только на изданной литературе, в том числе и преподавателей, работающих в ВлГУ, но и на статьях, опубликованных авторами в центральных и зарубежных журналах.

ЛЕКЦИЯ 1. Введение в курс дисциплины «Основы нанотехнологий». Масштабная шкала.
План лекции:
Ввести масштабную шкалу физических объектов. Рассмотреть примеры объектов микро-, макро-, мега- и наномира.
Определить положение нанообъектов на шкале масштабов микро- макро- и мегамира.
Рассмотреть перечень задач, решаемых нанотехнологией.
10-34)
10-29
10-15
10-10
( 10-9
10-7
)
(
10-6
100)
107
1012
( 1025

Масштабную шкалу расстояний в природе разделим на микро-, макро-, и мегамир. Расстояние в макромире, в котором существует человек, составляет в шкале число 100 метров. Из астрономии известно, что наиболее удаленные от нас галактики находятся на
расстоянии 14 млрд. световых лет. Эта величина приближенно определяет расстояние 1025 метра (иногда называемое «горизонтом событий»). Минимально известное расстояние 10-34 метра, определяется расчетным путем на основе так называемых планковских величин, полученных из комбинации основных констант в природе: h - потоянной Планка, G - гравитационной постоянной и c – скорости света. Сами эти константы входят в важнейшие физические формулы для энергии, характеризующей микро- макро- и мегамир:
E = mc2 ; E = hν ; Fгр = Gm1m2/r2; (Eгр = Gm1m2/r )
c, h, G – Метагалактика
Поэтому нашу Вселенную можно назвать c, h, G – Метагалактикой. В нее входят миллиарды миллиардов галактик, в том числе и галактика «Млечный путь», в которой находится наша Солнечная система.
Расстояния, характеризующие макромир, оценим в интервале от размеров крупных молекул (глобулы имеют средние размеры, равные 10-8м) до величины среднего расстояния от Солнца до внешних планет, измеряемое десятками астрономических единиц (до Земли 1 а.е., а до Плутона, например, около 40 а.е.). За основу анализа явлений в макромире примем эволюционный подход, базирующийся на теории инфляции и Большого взрыва, породившего в итоге элементарные частицы, а затем и химические элементы.
МЕГАМИР. Мегамир представим КОСМИЧЕСКИМИ ОБЪЕКТАМИ:
(фотографии телескопа «Хаббл»)

Галактика Сомбреро – в 28 миллионах световых лет от Земли – была признана лучшей фотографией, сделанной «Хабблом». Размеры галактики, официально названной М104, также впечатляющи, как и ее внешний вид. В нее входит 800 миллиардов звезд, и ее диаметр составляет 50000 световых лет.

Муравьиная туманность, облако пыли и газа, чьим техническим названием является Mz3, при наблюдении с земной поверхности напоминает муравья. Туманность расположена в нашей галактике на расстоянии от 3000 до 6000 световых лет.
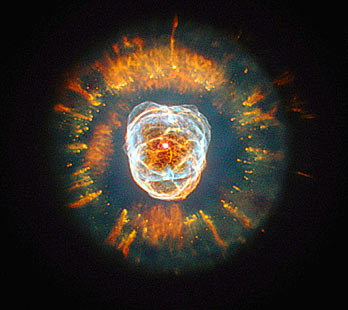
На третьем месте туманность NGC 2392, называемая Эскимосом, так как напоминает лицо, обрамленное меховым капюшоном. Капюшон на самом деле является кольцом кометообразных объектов, разлетающихся от умирающей звезды. Туманность Эскимос находится в 5000 световых лет от Земли.

На четвертом – туманность Кошачий глаз, напоминающая глаз бесплотного колдуна Саурона из «Властелина колец».

У туманности Песочные часы, в 8000 световых лет от Земли, пережатый в центре вид, так как ветра, придающие ей форму, слабее в центре.

Звездная ночь, названная так, потому что напомнила астрономам картину Ван Гога. Это гало света вокруг одной из звезд Млечного пути - V838 Единорога, вспыхнувшей в январе 2002 года. А потом она так же быстро стала угасать. Вспышка звезды подобного рода ранее не наблюдалась. Глядя на изображение вы видите лишь движущееся вдали от звезды световое эхо яркой вспышки. V838 Единорога находится на расстоянии 20 тысяч световых лет от нас в созвездии Единорога. Пылевые оболочки, обусловливающие явление светового эхо, составляют в диаметре около шести световых лет.

Светящиеся глаза на расстоянии 114 миллионов световых лет являются вращающимися ядрами двух сталкивающихся галактик NGC 2207 и IC 2163 в отдаленном созвездии Большого Пса.
МАКРОМИР. Рождение планеты Земля.
Теория, подробно рассматривающая процесс рождения Солнечной системы, называется конденсационной. В результате, Солнечная туманность, которая образовалась при взрыве сверхновой, отделившись от других туманностей Вселенной, могла принять вид газовой сферы с пылью из твердых частиц и с массой примерно равной сегодняшней массе Солнечной системы. Процесс дальнейшей эволюции теоретически может иметь три возможных сценария:
Вращательный момент сферы равен нулю, то есть, нет вращения. Тогда под действием гравитационного притяжения образуется единый объект – Солнце без планетной системы («глобулярная» модель).
Вращательный момент небольшой (скорость вращения невелика). Тогда основная часть вещества по прежнему концентрируется в центральном объекте – Солнце, а остальная часть остается в виде туманности, окружающей Солнце. По мере вращения этот “небулярный” газ постепенно принимает форму диска в плоскости, перпендикулярной оси вращения, а затем при понижении температуры концентрируется вокруг отдельных образований, имеющих средние размеры около 10 км. Эти образования названы планетезималями (зародышами планет), дальнейшая концентрация вещества вокруг которых приводит к окончательному формированию планет.
Большой вращательный момент. В этом случае сфера расщепляется (разлетается) на два “солнца”, а тогда образуются бинарные звезды.
Очевидно, что для нашей Солнечной системы оправдался второй сценарий.
НАНОМИР. Появление жизни на Земле оказалось возможным благодаря наличию углерода, возникающего в результате нуклеосинтеза легких элементов и благодаря процессам атмосферы, возможно, при резкой дегазации горных пород, т.е. как следствие вулканической деятельности. В этом процессе пары воды, выделяющиеся из недр высокотемпературной Земли, при охлаждении образовали первые океаны.
Существует также гипотеза о «космическом» происхождении воды на Земле, занесенной ледяными метеоритами, большое количество которых расположено в «поясе метеоритов», расположенном между Марсом и Юпитером. Свойства воды оказались уникальными и воду можно считать «колыбелью зародившейся жизни». Приведем пример теста КСЕ, в котором проверяется знание о некоторых свойствах воды. (Записываем).
Океанические воды стали постепенно поглощать молекулы CO2 из атмосферы, что привело к преобладанию в ней азота N2. Дальнейшее понижение температуры океана и поверхности Земли привело к началу химической эволюции от простейших молекул к все более сложным, от простых реакций взаимодействия между молекулами вплоть до появления принципиально нового химического процесса – матричного синтеза для биополимеров. Рассмотрим подробнее отдельные фрагменты химической эволюции.
Процессы, характеризующие химическую эволюцию на Земле, будем анализировать и на этот раз методом инверсии, так как экспериментальная проверка многих реакций в лабораторных условиях не всегда возможна.
Как известно, результатом этой эволюции явилось возникновение жизни, существующей на базе открытых самоорганизующихся систем, построенных из биополимеров. Эти слова могут быть положены в основу феноменологического определения жизни, как способа существования открытых самоорганизующихся систем, построенных из биополимеров. Основные отличия живого от неживого заключаются в появлении организменного состояния систем, в которых и сложные и простые химические структуры выполняют определенные функции, а протекающие химические (правильнее сказать физико - химические) реакции согласованы. Усложнение систем биополимеров приводит к появлению основы жизни организмов – к клетке.
В качестве примера клеточных процессов рассмотрим работу полирибосомного комплекса в клетке живого организма, функция которого заключается в синтезе белков. Рибосома представляет собой очень крупное молекулярное образование, которое состоит из двух субъединиц, в одной из которых содержится крупная молекула РНК (рибонуклеиновой кислоты) и около 30 различных белков, а в другой более мелкая молекула РНК и приблизительно 20 различных белков. Рибосомный комплекс выполняет две основные функции при синтезе белков. Первая связана с фиксацией начала “считывания кодонов” – триплетов из пуриновых и пиридиновых оснований, записанных на матричной РНК (мРНК). Напомним, что четыре “буквы”: А(аланин), У(урацил), Г(гуанин) и Ц(цитозин) могут образовать 64 варианта трехбуквенных сочетаний (кодонов), а именно, с 4-мя начальными буквами на первом месте, с 4-мя на втором и 4-мя на третьем, которые кодируют 20 аминокислот. Соотношение: 20 и 64 показывает, что некоторые аминокислоты кодируются неоднозначно.

Процесс присоединения транспортной РНК (тРНК), несущей к месту сборки белка определенную аминокислоту, показан на рис. 53. Молекула тРНК, несущая метионин, присоединяется к первому кодону (АУГ), а другая тРНК, несущая аланин, располагается рядом так, что между их концами образуется пептидная связь (групповая связь между молекулами, построенная на совокупности водородных связей). Образование этой связи происходит при участии рибосомного фермента. После того как метионин первой молекулы соединится с аланином второй, он отделяется от первой тРНК, которая отделяется от матрицы и отправляется “на поиски” следующей молекулы метионина. Справа от второй тРНК к матрице присоединяется третья тРНК, несущая серин и процесс повторяется. Затем присоединяется четвертая тРНК с лейцином и т.д. пока справа не присоединится “терминатор цепи”, на конце которого нет аминокислоты, способной к образованию соответствующих пептидных связей. На каждом этапе этого процесса рибосома перемещается по матрице и обеспечивает правильное присоединение тРНК, а также с помощью катализаторов ускоряет происходящие реакции. Когда рибосома достигает кодона – терминатора, она освобождается от матрицы вместе с построенной полипептидной цепью, которая принимает окончательную структурную форму. Ускорение синтеза и есть вторая специфическая функция рибосомного комплекса. В появившейся нанотехнологии, описываемые выше процессы, можно назвать процессами функционализации в природе, в отличии от нанотехнологических процессов функционализации в лаборатории или на производстве.
МИКРОМИР.
Подробный анализ структур микромира и их особенности рассмотрим в следующих лекциях. В то же время, подводя итоги, можно представить таблицу, описывающую уровни описания микромира от классических представлений до современного состояния.
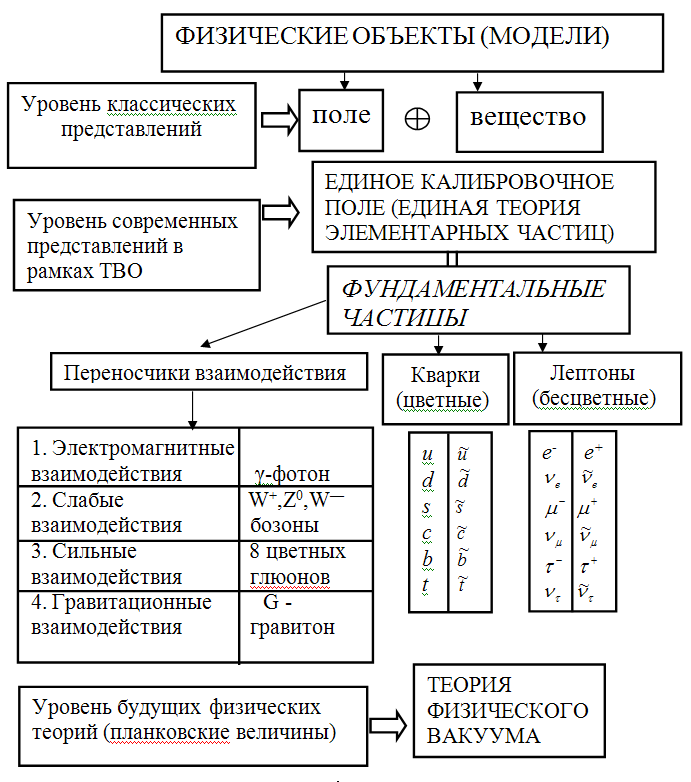
Итак, на лекции мы определили место нанотехнологии в системе существующих знаний о природе. Перечислим кратко основные задачи нанотехнологии.
Задачи нанотехнологии.
Разработка научных основ наноструктурных исследований для развития нанотехнологий и мониторинга технологических процессов.
Совершенствование методов наблюдения структуры вещества на наноуровне и соответствующего оборудования.
Разработка методов получения материалов с новыми свойствами, определяемыми структурой вещества на наноуровне.
Создание технологий получения наноматериалов с учетом требований экологии.
Создание веществ, устройств, материалов и продукции с потребительскими свойствами.
ЛЕКЦИЯ 2. Структура и свойства вещества. Атомно-молекулярная структура вещества. Электроны. Зонная теория. Деление веществ на проводники, диэлектрики и полупроводники. Размерные эффекты. Нанокластеры.
План лекции:
Рассмотреть примеры атомно-молекулярной структуры вещества.
Рассмотреть деление веществ на проводники, диэлектрики и полупроводники на основе зонной теории.
Ввести представление о нанокластерах и дать понятие о размерных эффектах.
СТРОЕНИЕ АТОМОВ И МОЛЕКУЛ.
1. Определим составные части атома.
2. Обсудим эксперимент Томсона по определению отношения заряда к массе электрона.
3. Рассмотрим опыты Резерфорда и структуру атома водорода по Бору
4. Построим энергетические уровни атома водорода. Введем представление о фотоне.
Историю возникновения самых общих представлений об атоме обычно ведут со времен греческого философа Демокрита (около 370 до н. э.), много размышлявшего о наименьших частицах, на которые можно было бы поделить любое вещество. Группу греческих философов, придерживавшихся того взгляда, что существуют подобные крошечные неделимые частицы, называли атомистами. Греческий философ Эпикур (около 342 до н.э.) принял атомную теорию, и в первом веке до н.э. один из его последователей, римский поэт и философ Лукреций Кар, изложил учение Эпикура в поэме "О природе вещей", благодаря которой оно и сохранилось для следующих поколений.
Первым действительно научным обоснованием атомистической теории, убедительно продемонстрировавшим рациональность и простоту гипотезы о том, что всякий химический элемент состоит из мельчайших частиц, явилась работа английского школьного учителя математики Дж.Дальтона, статья которого, посвященная этой проблеме, появилась в 1803г. Дальтон изучал свойства газов, в частности отношения объемов газов, вступавших в реакцию образования химического соединения, например, при образовании воды из водорода и кислорода. Он установил, что отношения прореагировавших количеств водорода и кислорода всегда представляют собой отношения небольших целых чисел. Массы кислорода, реагирующие с одной и той же массой водорода при образовании этих двух соединений, соотносятся между собой как небольшие числа: 16:32 = 1:2. На основе подобных результатов Дальтон сформулировал свой "закон кратных отношений". Согласно этому закону, если два элемента соединяются в разных пропорциях, образуя разные соединения, то массы одного из элементов, соединяющиеся с одним и тем же количеством второго элемента, соотносятся как небольшие целые числа. По второму закону Дальтона, "закону постоянных отношений", в любом химическом соединении соотношение масс входящих в него элементов всегда одно и то же. Большое количество экспериментальных данных, относящихся не только к газам, но также и к жидкостям и твердым соединениям, собрал Берцелиус, который провел точные измерения реагирующих масс элементов для многих соединений. Многочисленные опытные данные Берцелиуса подтвердили сформулированные Дальтоном законы и убедительно продемонстрировали наличие у каждого элемента наименьшей единицы массы.
Однако реальная структура атомов, в том числе и существование еще меньших частиц, составляющих атомы, оставалась неясной до открытия Дж.Дж.Томсоном электрона в 1897 году. Схема опыта изображена на рисунке.
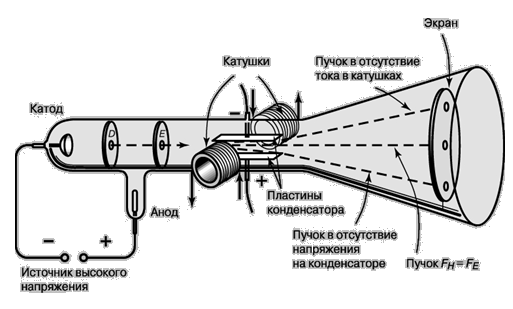
СХЕМА ОПЫТА ПО ОПРЕДЕЛЕНИЮ ОТНОШЕНИЯ ЗАРЯДА К МАССЕ ЭЛЕКТРОНА. Трубка, использованная английским физиком Томсоном для определения отношения заряда к массе для катодных лучей. Эти опыты привели к открытию электрона.
Электрическая сила FЭ действующая на заряд e со стороны электрического поля E, дается выражением FЭ= eE. Кроме того, в той же области трубки с помощью пары катушек с током могло создаваться магнитное поле, способное отклонять электроны в противоположном направлении. Сила FМ (сила Лоренца) действующая со стороны магнитного поля В, пропорциональна индукции магнитного поля, скорости частицы v и ее заряду e: FМ = Вev.
Этих двух соотношений оказалось достаточно для определения отношения заряда к массе частицы.
Еще раньше, Фарадеем в опытах по электролизу было обнаружено существование ионов с положительным и отрицательным зарядом, кратным некоторой величине. После опытов Томсона было доказано, что эта величина совпадает с зарядом электрона. Поэтому электрически нейтральный атом должен состоять из иона и электронов.
Окончательно, строение атома было открыто в опытах Резерфорда по рассеиванию положительно заряженных α-частиц на тонкой металлической фольге из золота. Рассеивание показало, что в атомах должно существрвать массивное положительное ядро малых размеров.
Схема опытов Резерфорда приведена на рисунке.
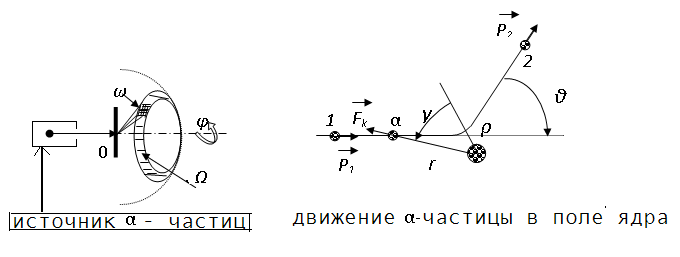
Для проверки распределения зарядов в атоме, Резерфордом был поставлен эксперимент по рассеянию частиц, пролетающих сквозь мишень. В качестве мишени была взята тонкая золотая фольга. Результаты подтвердили существование ядерной модели. В то же время, основываясь на классических законах механики и электродинамики, устойчивость такого атома должна быть недолговечной. Действительно, движение по окружности должно происходить с изменением скорости – направление движения все время меняется, а изменение скорости ведет к ускорению. Для планетарных систем и спутников такое движение может быть и устойчивым, но электрон – это не планета, он имеет заряд а неравномерное движение заряда равносильно переменному току или меняющемуся во времени электрическому полю. Порождается электромагнитная волна, которая уносит энергию в окружающее пространство. Так как эта энергия была порождена за счет движения электрона, то его кинетическая энергия должна убывать, скорость движения должна уменьшаться и электрон должен «упасть» на ядро. Атом прекращает свое существование. Его размеры становятся практически размерами ядра, которые оценивались по результатам опыта Резерфорда радиусом 10-15м.
Необычные свойства вещества в микромире потребовали и нового способа описания микрочастиц. Вначале, Планк создал квантовую теорию электромагнитного излучения, заменив волну на поток квантов (порций) с энергией Eγ = hν (h - постоянная Планка, а ν - частота излучения света). Затем Эйнштейн на основе этой теории объяснил необычные законы фотоэффекта и ввел для этого представление о реальной частице, которая была названа фотоном. Далее Нильс Бор использовал квантовую модель для объяснения процессов поглощения и излучения энергии атомами, то есть объяснил, каким образом «рождаются» кванты излучения – фотоны при переходе атомов из одного состояния в другое.
Теория Бора базируется на трех основных постулатах:
1. В атомной системе существуют такие стационарные состояния, находясь в которых атом не поглощает и не излучает эне6ргии;
2. Излучение и поглощение энергии при перехода атома из одного стационарного состояния в другое происходит порциями hν =ΔE.
3. Движение электрона происходит по разрешенным орбитам, момент импульса электрона, при этом, кратен целому числу ћ: mvrn = nћ, где n - квантовое число, равное 1, 2, 3, 4, … .
Для расчета величин энергии, радиуса орбиты и скорости движения электрона в атоме водорода решается система уравнений:
1. Второй закон Ньютона: mv2/r = k e2/r2;
2. Правило квантования момента импульса: mvnrn = nћ;
3. Полная энергия системы: En=mv2/2 – ke2/r.
Решая систему уравнений, получаем: En = - 1/n2 (me4/8ε02h2).
Расчет энергий состояний, в которых могут находиться атомы водорода, полностью объяснил эксперименты по спектральному анализу. Вот эти состояния (см.рисунок), которые нумеруются главным квантовым числом n, и их энергии, определяемые по формуле:
En = E1/n2; где E1 – отрицательная величина.
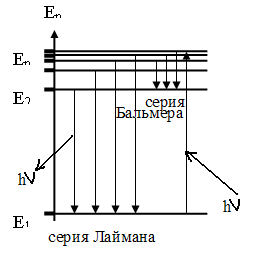
Рисунок. Схема энергетических уровней атома водорода
серия Лаймана , серия Бальмера
ΔЕ = Еm - Еn = hν (закон сохранения и превращения энергии).
Атом Фотон
Изменение энергии при переходе атома из одного состояния в другое «порождает» фотон, и наоборот, поглощенный фотон приводит атом в возбужденное состояние с большей энергией. Возбужденное состояние длится недолго, около 10-8с и атом, самопроизвольно, (или под действием другого фотона с той же энергией, при которой происходило возбуждение), возвращается обратно. Если атом возвращается обратно под действием фотона, поглощенного возбужденным атомом, то в результате появляются два фотона, согласованных друг с другом. Эти два могут быть поглощены еще раз возбужденным атомом, тогда излучается уже три фотона и т.д. Такой процесс, теоретически предсказанный Эйнштейном, называется индуцированным (наведенным) и используется при создании лазеров.
На этой стадии процесса изучения строения атома оставалось невыясненным, как движется электрон в атоме? На этот вопрос ответила зарождающаяся в это время квантовая механика.
При объединении атомов в молекулу, энергетические уровни «расщепляются», так как одинаковым электронам в одной системе нельзя находиться в одном состоянии. Это требование называется принципом Паули. Соответственно, при объединении молекул в структуру, которую можно назвать атомно-молекулярным кластером (нанокластером, наноструктурой, нанокристаллом)), количество электронных уровней с близкими значениями растет пропорционально числу обобщенных электронов. Наконец, при объединении атомов и молекул в твердое тело (кристалл), энергетические уровни объединяются в почти непрерывные «зоны», на которых распределяются электроны. Некоторые состояния (HOMO) будут заполнены электронами (с меньшей энергией), а некоторые (LUMO) – не заполнены (с большей энергией). При этом возможны три варианта соотношений между зонами, определяющими свойства соответствующего вещества:
Зоны заполненные электронами и незаполненные значительно отделены друг от друга. Такое вещество проявляет свойство «диэлектрика».
Зоны незначительно отделены, тогда вещество проявляет свойство «полупроводника».
Зоны не разделены или перекрываются, тогда вещество является «проводником» электрического тока.
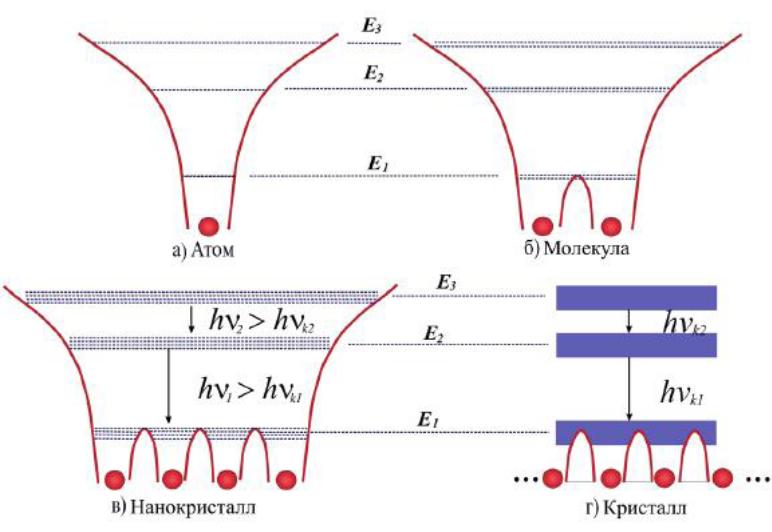
На рисунке для сравнения приведены варианты состояний атома, молекулы, нанокластера и кристалла.
Если величины энергий измерять в электронвольтах (эВ, eV), то оценочно, диэлектрик характеризуется энергетической «щелью» (HOMO-LUMO) ∆E > 5eV, у полупроводника –
∆E > 2eV<5eV, а у проводника - ∆E = 0 eV. Переходы между зонами и отдельными уровнями приводят к поглощению или излучению порций энергии ∆E = hν в виде фотонов. Очевидно, что излучение вещества в различных состояниях приводит к спектрам излучений (и поглощений) электромагнитных волн, которые определяются количеством атомов в системе, то есть зависимости свойств от размера атомно-молекулярной системы. Это различие называют «квантоворазмерным эффектом».

На рисунке показана зависимость окраски наночастиц от их размеров.
[по H. Weller (Institute of Physical Chemistry, University of Hamburg)]
С изменением размеров частиц происходят изменения и химической активности вещества. Эта зависимость названа «размерным эффектом», объяснение которого рассмотрим на практических занятиях.
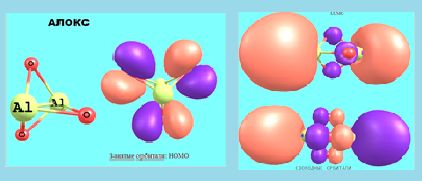
Большое значение при исследовании молекул и кластеров имеют квантовомеханические расчеты с помощью компьютеров, которые определяют распределение электронной плотности в пространстве. Одна из исследованных нами молекул алюмооксида (Алокса) представлена на рисунках, приведенных в заключение лекции.
ЛЕКЦИЯ 3. Электромагнитные основы нанотехнологии. Законы электродинамики. Электромагнитные волны. Фотонные кристаллы и голография.
Векторная модель электромагнитного поля позволяет дать описание основных экспериментальных фактов, связанных с объединением электрических и магнитных явлений в единую теорию (теорию Максвелла). Основные положения теории укладываются в систему дифференциальных уравнений Максвелла – Герца.
1. Вихревое магнитное поле в каждой точке пространства определяется токами проводимости и смещения (меняющимся во времени вектором индукции электрического поля) в этой же точке:
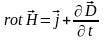 .
.
2. Вихревое электрическое поле в каждой точке пространства определяется меняющимся во времени вектором индукции магнитного поля в этой же точке:
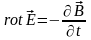 .
.
3. Источником расходимости электрического поля в каждой точке пространства является наличие в ней источника (заряда) с плотностью ρ :
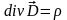 .
.
4. Ни в одной точке пространства магнитное поле не имеет источников расходимости:
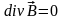 .
.
Часто используются в расчетах дополнительные соотношения, связывающие между собой отдельные параметры поля:
(а). Материальные
соотношения:
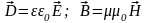 ;
;
(б). Закон Ома и уравнение непрерывности линий тока в проводнике:
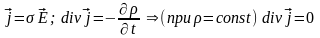 .
.
В однородной среде величины электрической и магнитной проницаемости, а также удельная проводимость постоянны (ε = const, μ = const, σ = const), поэтому учитывая материальные соотношения, уравнения Максвелла принимают вид:
1.
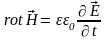 ,
2.
,
2.
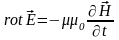 ,
3.
,
3.
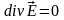 ,
4.
,
4.
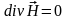 .
.
Применение к
полученной системе уравнений одной из
дифференциальных операций второго
порядка (двойной операции ротора),
позволяет разделить переменные
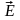 и
и
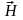 ,
затем приводит к двум независимым
уравнениям, определяющим поведение
электрического и магнитного полей в
пространстве и времени:
,
затем приводит к двум независимым
уравнениям, определяющим поведение
электрического и магнитного полей в
пространстве и времени:
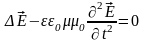 ;
;
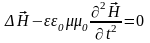 .
.
Решением этих уравнений, соответственно, являются функции вида:
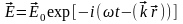 ,
,
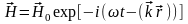 ,
,
которые
по формуле Эйлера (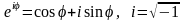 )
легко разложить на действительную и
мнимую часть, каждая из которых
представляет собой периодическую
функцию, являющуюся частным решением
волнового уравнения, что легко проверить
прямой подстановкой. Если, в частном
случае действительной компоненты
)
легко разложить на действительную и
мнимую часть, каждая из которых
представляет собой периодическую
функцию, являющуюся частным решением
волнового уравнения, что легко проверить
прямой подстановкой. Если, в частном
случае действительной компоненты
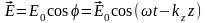 ,
зафиксировать координату z
(z
= 0), то функция будет описывать колебания
вектора напряженности в начале координат
с периодом Т
и частотой ω.
Действительно, при t0
= 0 Δt
= T
и по определению периода ωT
= 2π , то
,
зафиксировать координату z
(z
= 0), то функция будет описывать колебания
вектора напряженности в начале координат
с периодом Т
и частотой ω.
Действительно, при t0
= 0 Δt
= T
и по определению периода ωT
= 2π , то
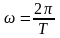 .
Рассуждая аналогично, при фиксированном
моменте времени (при «фотографировании»
процесса), получим в пространстве
периодическое распределение вектора
напряженности. Величина
.
Рассуждая аналогично, при фиксированном
моменте времени (при «фотографировании»
процесса), получим в пространстве
периодическое распределение вектора
напряженности. Величина
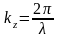 называется в данном случае волновым
числом, а в общем случае одной из проекций
волнового вектора
называется в данном случае волновым
числом, а в общем случае одной из проекций
волнового вектора
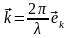 .
.
Так как процесс колебаний физической величины периодически распределенный в пространстве является определением волнового процесса, то полученные решения исходного дифференциального уравнения имеют право называться волновыми функциями, а дифференциальное уравнение волны – волновым уравнением. Таким образом, электромагнитное поле в вакууме существует в виде электромагнитной волны.
ЭЛЕКТРОМАГНИТНЫЕ СИГНАЛЫ. ПРЕОБРАЗОВАНИЯ ФУРЬЕ
При освещении
объекта электромагнитной волной, по
принципу Гюйгенса – Френеля, каждая
точка объекта с координатой x
становиться источником вторичных волн:
модулирует интенсивность падающей
волны в соответствии со своей рассеивающей
способностью ρ(xj)
и меняет фазу волны в соответствии с
координатой. В пространстве распространяется
вторичная волна, которая после усреднения
амплитуды по времени
может быть записана следующим образом:
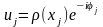 .
Если, для определенности, в качестве
объекта избрать дифракционную решетку,
то в пространстве образуется дифракционная
картина, порядки дифракции которой h,
заданные направляющими косинусами в
фиксированной системе координат, будут
характеризоваться интенсивностями,
полученными в результате сложения волн
от точек дифракционной решетки. Тогда
можно записать следующее выражение:
.
Если, для определенности, в качестве
объекта избрать дифракционную решетку,
то в пространстве образуется дифракционная
картина, порядки дифракции которой h,
заданные направляющими косинусами в
фиксированной системе координат, будут
характеризоваться интенсивностями,
полученными в результате сложения волн
от точек дифракционной решетки. Тогда
можно записать следующее выражение:
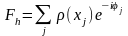 .
.
Если теперь на пути рассеянных волн с амплитудами Fh поставить собирающую линзу или любым другим способом (в том числе и математически) собрать (сложить) эти рассеянные волны, то мы снова получим образ объекта ρ(xj) в виде распределения в пространстве рассеивающих точек:
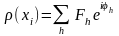 .
.
В общем случае, для произвольно взятого объекта величины координат и направляющих косинусов (проекций волнового вектора) меняются непрерывно, в фазу волны эти переменные входят симметрично (φj = φh=φ) , поэтому суммирование заменяется интегрированием. Выражения образуют пару соотношений, которые называются преобразованиями Фурье:
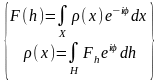 .
.
Так как экспоненциальная функция, входящая в эти преобразования может быть разложена по формуле Эйлера, то существуют косинусовое и синусовое преобразования Фурье. Выражения непрерывных преобразований Фурье. Функция F(h) называется «образом» функции ρ(x). Обобщение преобразований Фурье для трехмерного пространства является чисто техническим усложнением и может быть записано следующим образом:
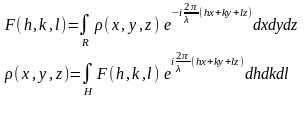 , где пространство
объекта R
задано векторами
, где пространство
объекта R
задано векторами
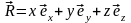 ,
а пространство образов H
задано волновыми векторами так называемого
«обратного пространства»
,
а пространство образов H
задано волновыми векторами так называемого
«обратного пространства»
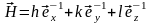 .
Числа h,k,l
иногда называют пространственными
частотами. Инверсия координат в
пространственной области равносильна
комплексному сопряжению в обратном
пространстве, так как в фазе замена
переменной x
на –x
приводит к появлению минуса перед
символом мнимой единицы:
.
Числа h,k,l
иногда называют пространственными
частотами. Инверсия координат в
пространственной области равносильна
комплексному сопряжению в обратном
пространстве, так как в фазе замена
переменной x
на –x
приводит к появлению минуса перед
символом мнимой единицы:
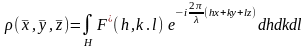 .
.
Символически,
после введения оператора фурье-преобразований
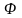 и обратных фурье-преобразований
и обратных фурье-преобразований
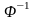 ,
формулы можно записать следующим
образом:
,
формулы можно записать следующим
образом:
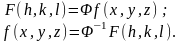
Все результаты, которые были выше рассмотрены для сигналов в пространственной области имеют аналогичные представления и во времени, так как фаза и амплитуда ЭМВ содержат симметричные пространственно-волновым (h,x) частотно-временные канонические переменные (ω,t). Поэтому, если зафиксировать координату или усреднить сигнал по пространственным переменным, то преобразования Фурье будут связывать между собой функции, зависящие от частоты и от времени:
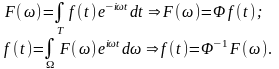
Соответственно в реальности, аппаратура для детектирования сигналов в этом случае отличается от аппаратуры для получения пространственных картин. В практике современного зондирования используются методы, основанные как на частотных (спектральных) характеристиках сигналов, так и на их пространственных (структурных) составляющих. Все чаще полнота полученной информации зависит от применения интегрального подхода в сочетании с вычислительными математическими методами обработки полученных в эксперименте данных. Картины рассеяния волн, а также эксперименты по интерференции и дифракции полностью описываются с помощью пары преобразований Фурье и приводят к уравнениям Лауэ и Вульфа-Брэгга, которые, в свою очередь, определяют оптические свойства фотонных кристаллов.
МЕТОДЫ ДИФРАКЦИИ
1.Метод Лауэ
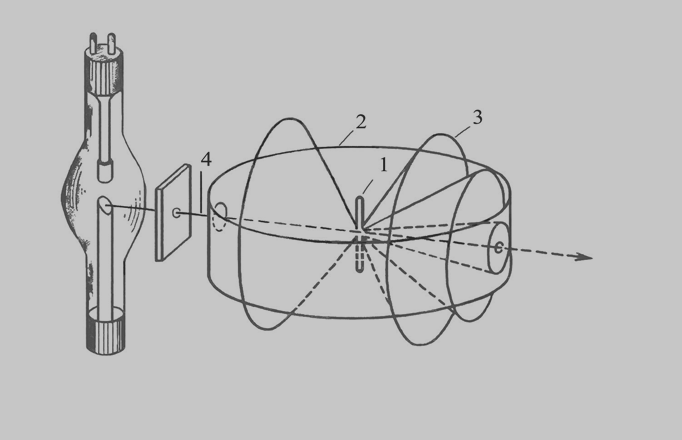
Уравнения Лауэ:
a (cosα – cosα0) = hλ;
b (cosβ – cosβ0) = kλ;
c (cosγ – cosγ0) = lλ.
Если направление рассеяния электромагнитных волн не удовлетворяют условиям Лауэ, то такие направления не могут распространяться. К такому же выводу приходим, если анализируем рассеяние ЭМ волн на атомных плоскостях (уравнения Вульфа-Брэгга).
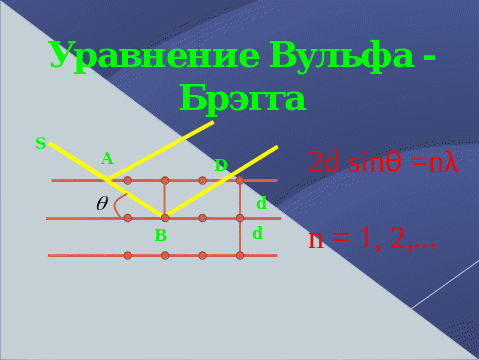

Если же длины волн, распространяющихся в кристалле удовлетворяют условиям Лауэ и Вульфа-Брэгга, то на фотоматериале фиксируется лауэграмма.
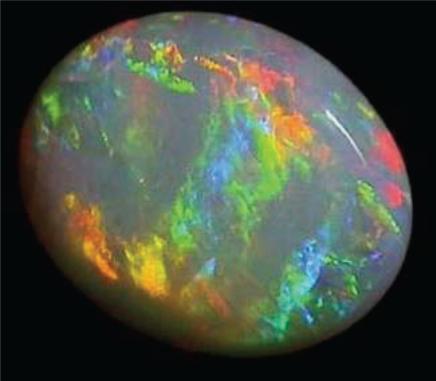

Природный фотонный кристалл – опал (рисунок слева) имеет периодическое внутреннее строение (справа), для которого также могут выполняться условия Вульфа-Брэгга. При этом, для различных направлений разные длины волн (цвет) могут оказаться и запрещенными. Этот факт объясняет зависимость окраски опала от угла, под которым производиться наблюдение.
Основы голографии.
Слово – голография – произошло от двух корней: голос, по-гречески означает «полный» или «весь», и графо – «пишу». Таким образом метод предполагает полную запись и восстановление трехмерного изображения объектов (нобелевская премия Денеша Габора 1960года). Простейшая схема голографии «на встречных пучках» с использованием ОКГ была предложена Ю.Н. Денисюком и позволяет получать при наличии высокоразрешающих фотоматериалов (записывающих до 6000 штрихов/мм) качественные трехмерные изображения реальных объектов. Метод основан на интерференции волн, идущих от объекта и от оптического квантового генератора (лазера).
|
Введем обозначения:
U1=U0eiφo - волна, идущая от источника к фотопластинке;
U2=U0eiφ - волна, идущая от предмета к фотопластинке;
U=(U1+U2) - результирующая волна в фотопластинке, при наложении (интерференции) волн U1 и U2.
После засветки и проявления на фотопластинке фиксируются почернения S(x,y,z), пропорциональные энергии результирующей волны, которая, в свою очередь, пропорциональна квадрату модуля волновой функции. Тогда S ~ Wэм ~ |U|2 = |U0eiφo+U0eiφ|2. Для комплексной функции квадрат ее модуля по правилам математики вычисляется как произведение самой функции на комплексно-сопряженную к ней. Следовательно, после замены i на -i (операция комплексного сопряжения), имеем:
S ~ (U0eiφo + U0eiφ)(U0e-iφo + U0e-iφ) =2U02 + U02ei(φo-φ) + U02ei(φ - φo).
При этом получается, что распределение почернений на фотопластинке содержит информацию о фазах волны, идущей от предмета к фотопластинке, что принципиально отличает голограмму от обычной фотографии объекта
(действительно, почернение S при обычном фотографировании определяется величиной |U1|2 = (U0eiφ)(U0e-iφ) = U02, то есть информация о фазах потеряна).
При восстановлении изображения объекта с помощию волны U1, идущей от источника, записанные на голограмме почернения модулируют падающий на них свет. В этом случае можно записать:
S·U1 = (2U02 + U02ei(φo-φ) + U02ei(φ - φo))·U0eiφo = 2U03eiφo + (U03ei2φo) e-iφ + + U03eiφ = A1eiφo + A2 e-iφ +A3eiφ.
Полученный результат показывает, что в пространстве восстановятся три волны: первая - идущая от источника с фазами φ0, вторая - предметная, с фазами -φ и третья - предметная с фазами φ, соответствующими волне U2, являющейся изображением объекта. Интересно отметить, что вторая волна может быть интерпретирована как изображение предмета, у которого произошла замена оси Ox на ось -Ox. Действительно, если вспомнить, что фаза φ = (ωt - kx) в случае плоской волны, то фаза –φ = (ω(-t) – k(-x)) в пространственной области будет иметь зеркальное отображение, так как x→(-x). Все выпуклое становится вогнутым. Чтобы увидеть это изображение, достаточно повернуть голограмму другой стороной по отношению к падающему от источника свету.
Неспециализированный эксперимент получения голограмм в условиях обычного образовательного учреждения. В качестве источника света используется гелий-неоновый лазер (ОКГ), который представлен на рисунке. Для получения светового пятна небольших размеров (диаметром до 10см) используем линзу с фокусным расстоянием F ~ 20см.
Расстояние от источника до объекта подбирается таким образом, чтобы объект "купался" внутри светового пятна. Основное требование к установке заключается в том, чтобы объект не смещался относительно фотопластинки, для чего штатив устанавливается на массивной металлической плите и при съемке объект слегка прижимается к эмульсионной стороне будущей голограммы. После засветки (время экспозиции измеряется для "свежих" пластин одной или несколькими секундами) и проявления, с использованием стандартных проявителей и фиксажа для обычной фотографии, голограмму сушат на воздухе при комнатной температуре. При проявлении можно использовать темнозеленый свет фонаря, так как специальные промышленные мелкозернистые (~ 6000 штрихов/мм) фотопластинки чувствительны к красной области спектра. Иногда объемные свойства голограмма приобретает только после сушки. Наблюдать голограммы следует в отраженном свете от любого проектора или в солнечных лучах.

Голограмма, полученная студентами в рамках НИРс ВлГУ.
Г олографические
методы получения фотонного кристалла.
В отличие от многих методов, где после
экспонирования образца излучением
часть вещества вытравливается, в
голографии не используется удаление
вещества. Фоточувствительный материал
вносится в поле интерферирующих лучей,
и в местах наибольшей интенсивности
света происходит его химическая
модификация. Это, в свою очередь, приводит
к пространственной зависимости показателя
преломления. Данным методом можно
получать кристаллы с пространственным
периодом, равным периоду записывающей
световой волны. Важным требованием в
голографии является когерентность
записывающих лучей, для обеспечения
которой необходимо конструировать
сложные оптические системы. Оптическая
система для создания фотонных кристаллов
методами голографии (заготовка помещается
сверху, в перекрестье 4-х лучей).
олографические
методы получения фотонного кристалла.
В отличие от многих методов, где после
экспонирования образца излучением
часть вещества вытравливается, в
голографии не используется удаление
вещества. Фоточувствительный материал
вносится в поле интерферирующих лучей,
и в местах наибольшей интенсивности
света происходит его химическая
модификация. Это, в свою очередь, приводит
к пространственной зависимости показателя
преломления. Данным методом можно
получать кристаллы с пространственным
периодом, равным периоду записывающей
световой волны. Важным требованием в
голографии является когерентность
записывающих лучей, для обеспечения
которой необходимо конструировать
сложные оптические системы. Оптическая
система для создания фотонных кристаллов
методами голографии (заготовка помещается
сверху, в перекрестье 4-х лучей).
ЛЕКЦИЯ 4. Методы исследования нанообъектов. Масс-спектроскопия. Растровый электронный микроскоп. Атомно-силовой микроскоп. Рентгеновские дифрактометры. Туннельный микроскоп.
Одним из экспериментальных методов получения структур нанокластеров является лазерная абляция, то есть удаление вещества с его поверхности под действием лазерного излучения. При мощном импульсном воздействии с поверхности наряду с испаряющимися атомами вещества вылетают целые кластеры. Затем поток гелия (см. рисунок) захватывает их и расширяется с охлаждением, выходя через сопло в вакуум. Уже в вакууме кластеры подвергаются воздействию УФ - излучения и ионизируются. Остальные задачи по разделению выполняет масс-спектрометр, в котором, в частности, под действием магнитного поля ионизированные кластеры распределяются по массам.
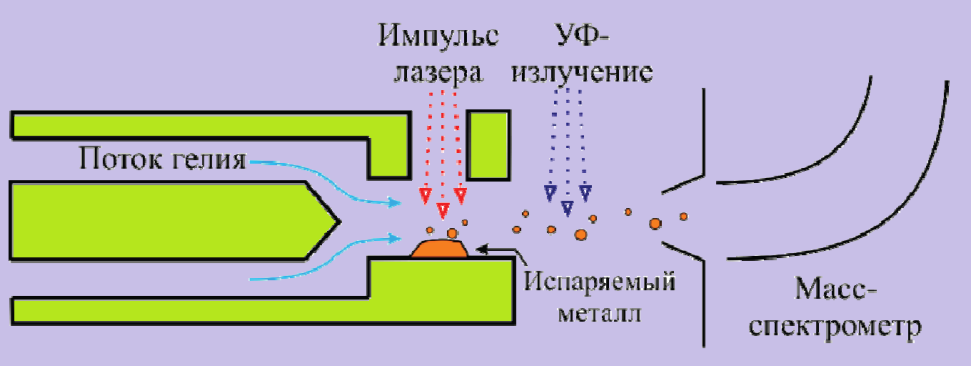
Принципиальная схема установки для проведения масс-спектрометрических исследований.
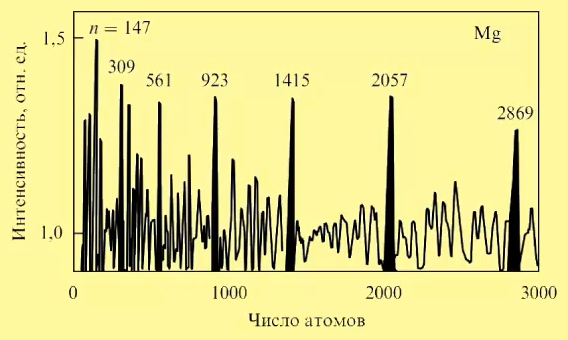
Масс-спектрограмма магния.
На рисунке приведена диаграмма распределения кластеров магния, полученная методом масс-спектроскопии. Выделенные над максимальными пиками числа называют «магическими». Они соответствуют устойчивым нанокластерам.
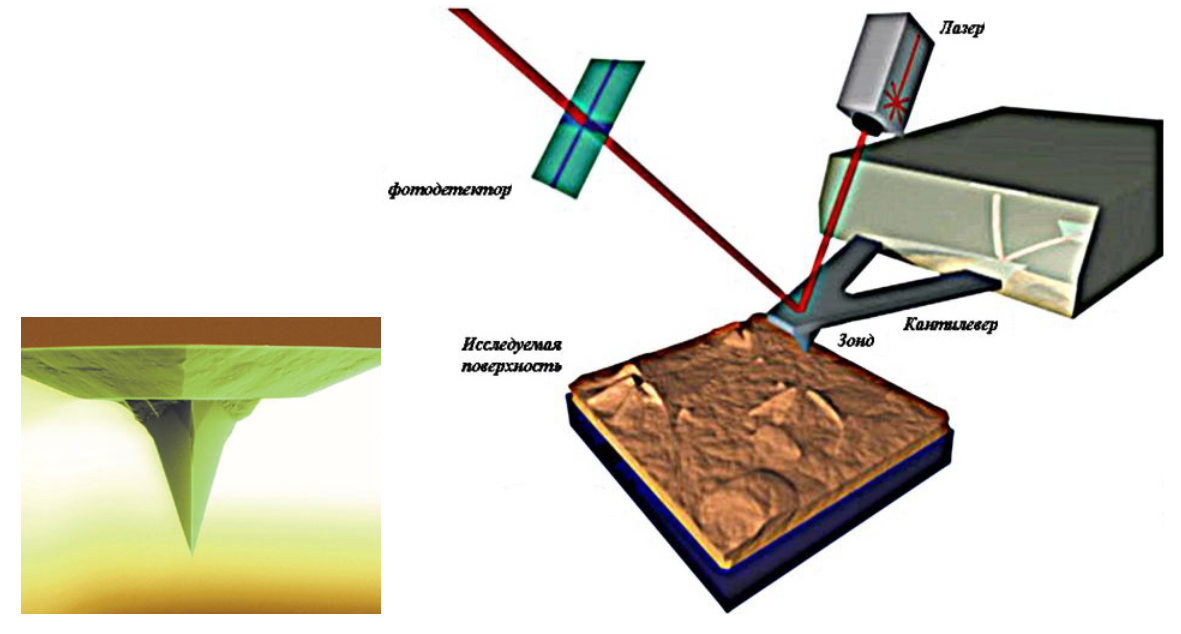
Атомно-силовой (сканирующий) микроскоп способен не только определять качество поверхности (до 1нм), но и захватывать отдельные атомы и молекулы, производя при этом сборку нанокластеров (см. рисунок).

Сборка нанокластеров ксенона на поверхности кремния

Поверхность анодированного алюмооксида в АСМ.

Растровый электронный микроскоп.

Снимок поверхности пористого анодированного алюмооксида. Размеры стенок пористой структуры приведены в нанометрах.

Рабочая часть рентгеновского дифрактометра фирмы «Брукер».
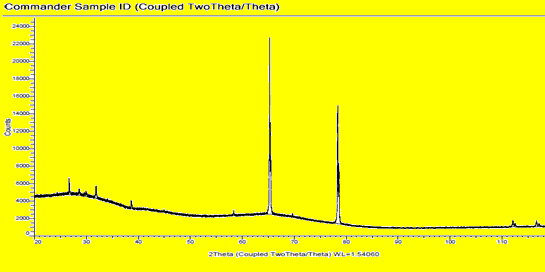
Результаты, проведенного с помощью дифрактометра анализа фазового состава анодированного алюмооксида.
Принцип работы туннельного микроскопа основан на решении кантовомеханической задачи на решение уравнения Шредингера, описывающего поведение микрообъектов в частности, электронов в электростатическом поле. Исторически, эта задача впервые решалась для частицы в ядре, для которой можно упростить решение, приняв потенциальную энергию в форме «потенциального барьера».
Решение этой задачи, впервые рассмотренной Г.Гамовым, привело к открытию «туннельного эффекта».
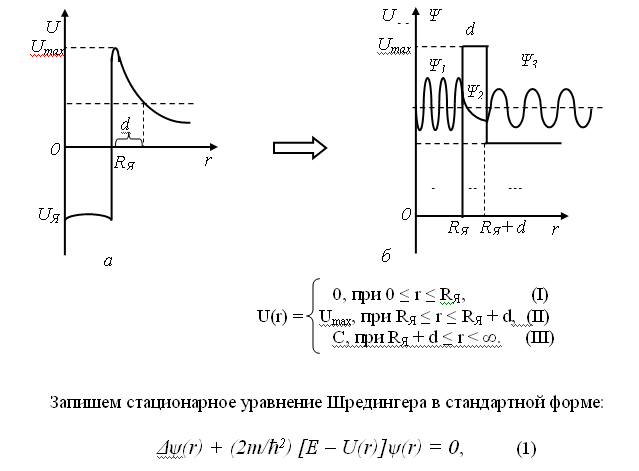


Атомно-силовой микроскоп может работать в режиме «туннелирования». Между иглой микроскопа и поверхностью , вследствие их близости, появляется туннельный ток.
 Магнитный
зонд спин-поляризованного сканирующего
туннельного микроскопа анализирует
магнитные свойства отдельных атомов.
Магнитный
зонд спин-поляризованного сканирующего
туннельного микроскопа анализирует
магнитные свойства отдельных атомов.
ЛЕКЦИЯ 5. Нанообъекты. Пути создания нанообъектов. Самоорганизация нанообъектов: «снизу-вверх». Наноструктурный анализ по дифракционным данным.
Процесс кристаллообразования представляет собой зарождение новой фазы кристаллических зародышей нанометрового размера «снизу-вверх», путем самоорганизации. Кристаллическая фаза характеризуется периодическим распределением вещества в пространстве, то есть, с точки зрения симметрии, является состоянием решетки. Рассмотрим вначале феноменологический подход к образованию кристаллического зародыша новой фазы в виде «нанокапли», включающей в себя несколько сотен атомов (молекул). В этом случае можно увидеть аналогию с капельной моделью атомного ядра Френкеля-Бора, но в которой близкодействие частиц определяется не сильным (ядерным) взаимодействием, а межмолекулярными силами. В гомогенном приближении, считая атомы или молекулы одинаковыми, величина энергии связи анализируемой термодинамической системы запишется как сумма «объемной» и «поверхностной» энергии следующим образом через средний радиус «нанокапли» R или через L –размер ребра кубика, если рост упрощенно рассматривать как объединение капель-«кубиков».
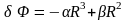 ,
,
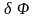 =
aL3+bL2 ,
=
aL3+bL2 ,
где
– изменение энергии системы
(термодинамического потенциала) при
переходе
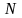 молекул (атомов, кластеров, …) из
несвязанного состояния (в среде) в
связанное (в кристалле), то есть энергия
связи;
молекул (атомов, кластеров, …) из
несвязанного состояния (в среде) в
связанное (в кристалле), то есть энергия
связи;
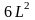 ,
,
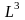 ,
соответственно, площадь поверхности
куба и объем куба.
,
соответственно, площадь поверхности
куба и объем куба.
Количество связей, то есть координация одной частицы равна 6, если кристалл строится из элементарных кубиков, соседствующих (связанных) друг с другом по граням. Это так называемая классическая модель роста Косселя, Странского, Каишева, Фолмера и других.
При атомно-молекулярном
подходе, число связей поверхностных
атомов в крупном ассоциате (агрегате)
при полном количестве частиц
существенно зависит от формы агрегата.
При определении скорости образования
зародышей (вероятностей
зарождения)
пользуются, как и при макроскопическом
подходе, расчетом минимальной работы
отрыва частиц
![]() от агрегата, то есть работой по преодолению
межмолекулярного взаимодействия. В
начале кристаллизации убыль энергии
взаимодействия будет характеризовать
переход к устойчивому процессу роста.
Основную роль в этом процессе будет
иметь размеры зародыша, определяемые
при росте кристалла конкуренцией
между поверхностной и объемной энергиями.
от агрегата, то есть работой по преодолению
межмолекулярного взаимодействия. В
начале кристаллизации убыль энергии
взаимодействия будет характеризовать
переход к устойчивому процессу роста.
Основную роль в этом процессе будет
иметь размеры зародыша, определяемые
при росте кристалла конкуренцией
между поверхностной и объемной энергиями.
Теплота
кристаллизации
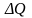 ,
измеряемая экспериментально,
характеризуется той частью энергии
системы, которая не является связанной
и может быть выделена (или поглощена) в
виде изменения энергии системы при
росте зародыша. Поэтому, используя
капельную молекулярную модель и первую
формулу, при условии
,
измеряемая экспериментально,
характеризуется той частью энергии
системы, которая не является связанной
и может быть выделена (или поглощена) в
виде изменения энергии системы при
росте зародыша. Поэтому, используя
капельную молекулярную модель и первую
формулу, при условии
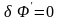 будем
иметь:
будем
иметь:
.
Максимум функции
(см.рисунок) определяет высоту
энергетического барьера (в точке
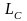 ),
преодоление которого ведет к уменьшению
энергии, и следовательно, к устойчивому
росту зародыша кристалла.
),
преодоление которого ведет к уменьшению
энергии, и следовательно, к устойчивому
росту зародыша кристалла.
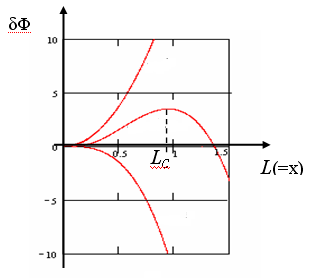
. Энергетический барьер процесса роста, как результат сложения отрицательной объемной и положительной поверхностной энергий связи
Метрическая модель послойно-секториального роста.
Представленные выше примеры моделей зарождения нанокапель, как термодинамические, статистические так и структурные, рассматриваемые на атомно-молекулярном уровне, не объясняют зарождения порядка, трансляционной симметрии и последующих процессов роста с сохранением самоподобия, то есть всего того, что характеризует кристаллическое состояние и его образование. Наиболее полно в науке рассмотрен лишь процесс роста отдельных граней, основанный на дефектах, в то время как закон постоянства углов, то есть проблема согласования роста граней, пока еще не решена. Кроме этого, очевидна ограниченность применения классической модели Косселя для молекулярных кристаллов, так как различные вещества реально приводят к отличающимся друг от друга многогранникам роста, а координационные связи, имеют в этой модели для всех структур одно и то же координационное число (равное шести). Такая жесткость модели не может объяснить разнообразия форм роста, или скорее, учесть индивидуальность каждого конкретного гомомолекулярного кристалла, а тем более кристаллов гетеромолекулярных соединений.
Исходную
идею геометрического подхода
послойно-секториального роста,
расширяющего возможности описания
различных структур, легко понять, если
сравнить процессы роста в условиях
«термодинамического беспорядка» и в
условиях «порядка». При структурном
хаосе движения молекул, в котором
равноправны все направления (при
изотропности внешних условий), рост
может привести к усреднению параметров
движения межфазной границы и появлению
окончательной формы в виде сферы:
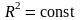 (изотропность). С другой стороны, в
упорядоченном периодическом пространстве
в самой сути состояния решетки заложена
анизотропия. Поэтому является вполне
естественным вопрос: «что собой
представляет «сфера» в дискретном
периодическом пространстве?». В качестве
ответа на этот вопрос рассмотрим сферу
координационную, так как именно
координация (ближайшее окружение), в
общем случае, анизотропна, дискретна,
индивидуальна и не противоречит
кристаллическому состоянию с трансляционной
симметрией. Однако эту координацию
нужно рассматривать не как некоторое
образование в комплексных соединениях,
в которых лиганды окружают
ядро-комплексообразователь, а как
межкомплексную, межмолекулярную,
межагрегатную, межкластерную и т.д.
координацию, переходя, очевидно, на
нанометровый уровень.
Кроме того, так же как обычную сферу
можно считать равновесной формой роста,
так и координационную
сферу логично
считать равновесной (идеальной) формой
роста в дискретном периодическом
пространстве. Построим координационную
сферу в периодическом пространстве.
(изотропность). С другой стороны, в
упорядоченном периодическом пространстве
в самой сути состояния решетки заложена
анизотропия. Поэтому является вполне
естественным вопрос: «что собой
представляет «сфера» в дискретном
периодическом пространстве?». В качестве
ответа на этот вопрос рассмотрим сферу
координационную, так как именно
координация (ближайшее окружение), в
общем случае, анизотропна, дискретна,
индивидуальна и не противоречит
кристаллическому состоянию с трансляционной
симметрией. Однако эту координацию
нужно рассматривать не как некоторое
образование в комплексных соединениях,
в которых лиганды окружают
ядро-комплексообразователь, а как
межкомплексную, межмолекулярную,
межагрегатную, межкластерную и т.д.
координацию, переходя, очевидно, на
нанометровый уровень.
Кроме того, так же как обычную сферу
можно считать равновесной формой роста,
так и координационную
сферу логично
считать равновесной (идеальной) формой
роста в дискретном периодическом
пространстве. Построим координационную
сферу в периодическом пространстве.
Как известно, поверхность обычной сферы в непериодическом пространстве формально определяется как множество точек, находящихся на эквидистантном расстоянии от одной точки (центра). Поэтому построение координационной сферы также можно начинать с понятия эквидистантности, но в периодическом пространстве. На рисунке представлен конкретный пример поиска части поверхности координационной «сферы» в секторе двумерного дискретного пространства, разбитого на квадраты (точки дискретного пространства). Произвольно выбранные девять шагов по геодезической, определяющей оптимальное число шагов между двумя точками в этом пространстве, выделяют целый набор «точек», отмеченных от точки, расположенной в начале координат штриховкой.
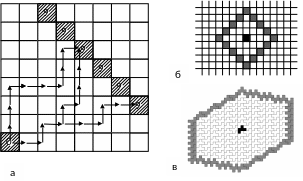
К определению формы роста.
Введем обозначение КЧП, что буквально означает – координационная числовая последовательность.
Если рассмотреть все четыре сектора роста, то можно увидеть образовавшийся на плоскости многоугольник роста в виде квадрата ( то есть, проведена координационная окружность «радиусом», равным четырем). Легко проверить простым построением, что при увеличении «радиуса» (числа шагов по геодезической) образовавшаяся форма растет самоподобным образом.. На следующем рисунке в дискретном пространстве, разбитом на молекулы-полимино по тому же принципу выбора эквидистантности точек, выделен шестиугольник роста (координационная окружность, проведенная «радиусом», равным семи). Индивидуальность формы полимино сказалась на полученном результате.
Компьютерный вариант трехмерной модели послойно-секториального роста представляет собой радиальный алгоритм последовательной сборки трехмерного полиэдра, производимой слой за слоем из элементов упаковки структуры (атомов, молекул, кластеров и т.д.), входящих в элементарную ячейку. Каждый элемент в программе заменен точкой – вершиной графа соседства кластеров, а выбранные в соответствии с анализом взаимодействия связи являются ребрами этого графа.
Применение трехмерной программы сборки показало, что как для модельных, так и для реальных структур результаты зависят от того, на какие фрагменты разбивается содержимое ячейки и какова координация каждого фрагмента. Этот этап был назван кластеризацией ячейки. Для некоторых исследованных структур комплексных соединений с карбамидом процедура разбиения содержимого ячейки на электростатически нейтральные кластеры, определила формы нанометровых зародышей, представленные на следующем рисунке.
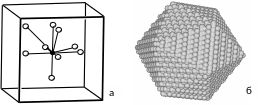
Рисунок
3D.
Модельная структура из 10 «атомов» в
ячейке (а) и соответствующая наноструктура,
представленная почти правильным
икосаэдром (б).
КЧП: 15, 33, 81, 177, 293, 399, 543, 795, 1173,….

При расчетах конкретного многогранника роста, центр масс каждой кластерной формы заменяется «цветной» точкой таким образом, чтобы координация точек (граф соседства) соответствовала разбиению ячейки на кластеры. Для любого из вариантов кластеризации в программе предусмотрен расчет «магических» чисел (КЧП) заполнения координационных сфер точками, которые для простейших многогранников отражают принцип плотнейшей упаковки кластеров и определяют дизайн поверхности каждой грани роста.

21-я
сфера из 1766 точек (а) и 15-я сфера из 1352
точек (б), полученные при расчете
нанометровых полиэдров роста,
соответственно, в структурах комплексных
соединений
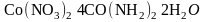 (КЧП:
6,10,38,34,102,74,198,130,,..) и
(КЧП:
6,10,38,34,102,74,198,130,,..) и
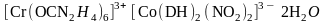 (КЧП: 8, 26, 56, 98, 152,..) .
(КЧП: 8, 26, 56, 98, 152,..) .
Очевидно, что физико-химические закономерности определяют взаимодействие молекул, взаимодействие определяет координацию, а координация определяет геометрию разбиения (или упаковки) пространства на исходные единицы, имеющие форму. Поэтому, зная атомную структуру и вид реального многогранника роста, можно определить из каких координирующих связей все это могло быть построено. При полноте перебора, получении «спектра решений», выбираем полиэдр, совпадающий с реальным многогранником. Вполне возможно, что при учете всех связей в структуре, равновесную форму роста нанозародыша будет характеризовать весь спектр вычисленных многогранников.
Ниже приведено несколько примеров реальных и модельных наноструктур, часть которых соответствует упаковочным многогранникам роста реальных кристаллов. Как показывает компьютерное моделирование, начиная с некоторого момента, индивидуального для каждой структуры, появляется четкая периодичность структуры, образующая волны координационной плотности. Так как образующаяся форма многогранника равновесная, то и плотность расположения молекул на гранях многогранника роста максимальна.
в
б
а
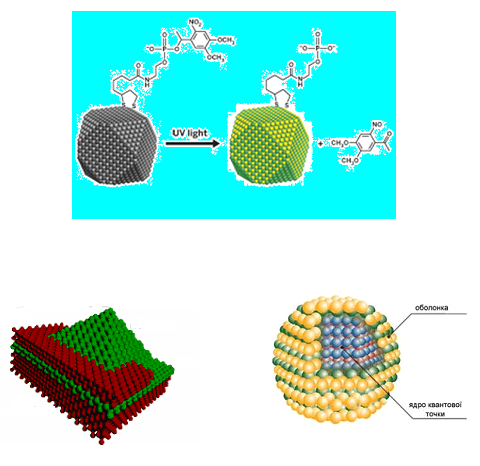
Примеры изображения наноструктур кристаллических зародышей (квантовых точек) по различным литературным источникам: (а) CdSe и органическая молекула; (б) пирамидка Ge на кремниевой платформе; (в) квантовая точка CdS .
Компьютерная сборка наноструктур моноклинной и ромбической серы, а также последующий рост многогранников, определяемых упаковкой молекул серы S8 в реальных структурах, показаны на рис.50.
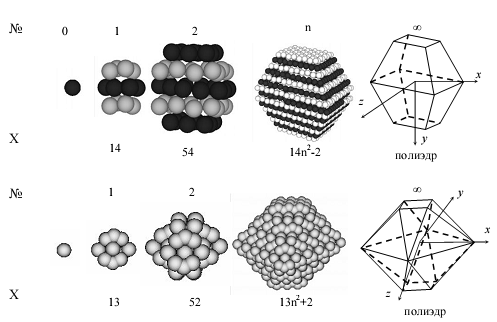
Последовательность заполнения молекулами координационных сфер моноклинной (а) и ромбической (б) серы (№ - номер координационной сферы, Х – количество молекул на поверхностях сфер).
При таком способе моделирования принципиально решается проблема совместимости веществ на основе их структурного соответствия, как часть исследований взаимодействий кристаллов с молекулами, кристаллов с кристаллами или наноструктур с наноструктурами и кристаллами. Создавая наносхемы, моделирующие элементы радиотехнических систем (фрактальных наноантенн, сверхрешеток, транзисторов и т. п.) и производя соответствующие расчеты физических характеристик этих установок, получаем инструмент для проектирования в наноэлектронике.
На следующем рисунке представлен результат компьютерной имитации процесса посадки наноструктуры антрацена, обладающего полупроводниковыми свойствами, на модельную платформу так, как если бы его можно было реально провести с помощью манипулятора в атомно-силовом микроскопе. Наноструктура антрацена рассчитана, так же, как и для серы, на основе знания координаций молекул антрацена, полученных из результатов исследования этого вещества методами рентгеновского дифракционного анализа.
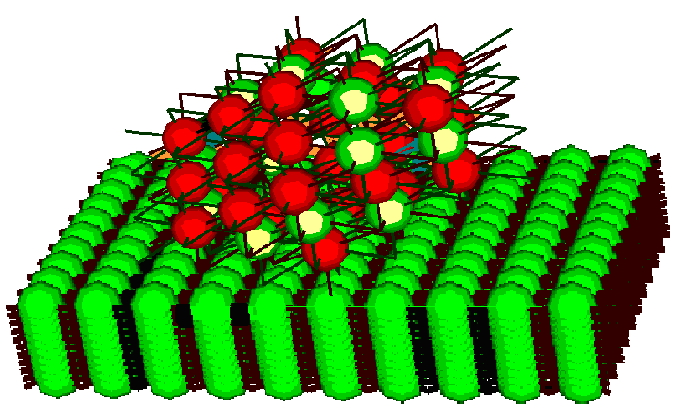
Имитация «посадки» наноструктуры антрацена на модельную платформу. Черным цветом показаны нескомпенсированные внешние координационные связи на поверхности антрацена.
Решая многоцентровую задачу роста зародышей при массовой кристаллизации, получаем результаты, которые отображаются в трехмерном пространстве так, как это показано наследующем рисунке.

Компьютерное моделирование роста наноструктур при массовой кристаллизации (многоцентровая задача роста).
В заключение кратко остановимся на основных отличиях наноструктурного состояния вещества от микро- и макроструктурного. Для наноструктур существенную роль играют два основных фактора.
Первый заключается в том, что отношение количества поверхностных молекул к их числу в объеме больше или соизмеримо с единицей, поэтому физико-химические свойства, в основном, определяются поверхностными молекулами. По числовым данным, приведенным на рис. 47, 48, 49 для количества точек (молекул) на поверхностях (КЧП), легко вычислить, что до четвертого координационного окружения в последовательности чисел соблюдается соотношение: X4 ≈ X3 + X2 + X1. После четвертого окружения количество молекул в объеме, как правило, превышает их число на поверхности. Если каждое последующее окружение отстоит от предыдущего на величину одного периода решетки, а средний период решетки молекулярных кристаллов составляет примерно 1нм, то линейный размер наноструктуры (диаметр) составит величину, равную 8нм. Таким образом, первый фактор играет существенную роль для наночастиц размерами (округляя) около 10нм.
Вторым, не менее существенным фактором является эффект размерного квантования состояний и энергетических уровней, о котором мы говорили во 2-й лекции. При уменьшении числа частиц, ограниченного размерами структуры агрегата, зонная теория крупных полупроводниковых материалов перестает давать правильные результаты. При анализе распределения фермионов (электронов) в металлах энергетический уровень зоны, заполненной электронами, определяется энергией Ферми, которая, в свою очередь соответствует концентрации частиц. При переходе к полупроводникам концентрация носителей (электронов и дырок) резко уменьшена и между зоной заполненной электронами и зоной проводимости появляется зона запрещенных энергетических состояний.
Уменьшение числа частиц в системе до нескольких десятков молекул, то есть переход к наноструктурам, приводит к увеличению этой энергетической щели. Вид валентной зоны и зоны проводимости так же меняются, больше напоминая молекулярные спектры. Если внутри полупроводниковой наноструктуры (часто называемой квантовой точкой) c n - типом проводимости внедрены «дефектные» слои из группы атомов с дырочной проводимостью, то образуются связанные состояния электрон-дырка, которые называются экситонами. Может образовываться экситонное состояние и на основе перехода слабо связанного электрона с массой me из зоны валентной в зону проводимости под действием фотона. На его месте образуется дырка с массой mg, с которой электрон взаимодействует. Всякая связь приводит к смещениям электронных уровней и в простейшей модели расчет показывает, что для экситона энергетические уровни смещаются до разности уровней ΔE:
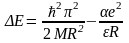 ,
,
где R
– средний размер квантовой точки, а
величина
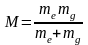 .
Из формулы (2.12.3) видно, что при малых
размерах частицы квантово-размерный
эффект расщепления уровней велик, а при
больших становится мало заметным.
.
Из формулы (2.12.3) видно, что при малых
размерах частицы квантово-размерный
эффект расщепления уровней велик, а при
больших становится мало заметным.
Эффект размерного квантования был обнаружен в экспериментах по наблюдению экситонного (электронно-дырочного) спектра, полученного от кристаллических наноструктур CdS.
Для проведения экспериментов применяется способ приготовления реальных полупроводниковых наночастиц в различных матрицах. Эти матрицы можно рассматривать как нанокамеры, ограничивающие предельный размер роста кристаллических кластеров. Так, например, в матрице из кристаллов цеолита диаметр нанокристаллитов определяется размером пор (в цеолите он обычно составляет величину около 2 нм). Для получения CdS в цеолите катионы натрия в цеолите заменялись катионами кадмия путем обработки цеолита водным раствором Cd(NO3)2 при рН = 5. Затем через образец пропускался газообразный сероводород (H2S).
В зависимости от содержания ионов кадмия в цеолите можно получить различные размеры кластеров CdS. При низких значениях отношения металл: :сероводород (1 : 1) образовывались кластеры CdS со средним размером менее 1,3 нм. В оптическом спектре от них наблюдался экситонный пик поглощения вблизи λ = 280 нм. При избытке кадмия индивидуальные кластеры объединяются в агрегаты с увеличенной структурой, заполняя внутренние полости цеолита. Это приводило к изменению оптического спектра, когда экситонный пик наблюдался вблизи участка спектра с длиной волны λ = 350 нм, что примерно соответствовало кластерам CdS диаметром 2,8 нм. Теоретическое исследование и изучение свойств наноструктур приведет к более широкому развитию нанотехнологии.
ЛЕКЦИЯ 6. Нанообъекты. Пути создания нанообъектов. Внешнее воздействие: «сверху-вниз»). Фуллерены.
План лекции:

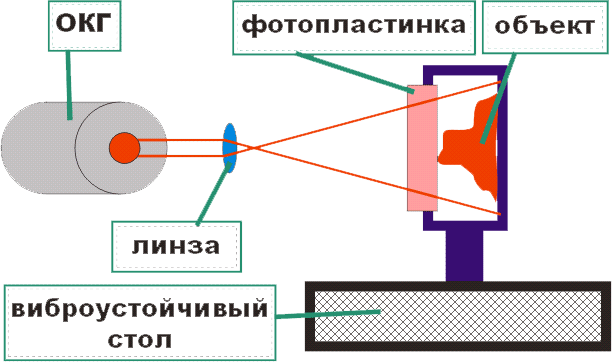 Схема
опытов по голографии. Метод Денисюка.
Схема
опытов по голографии. Метод Денисюка.