Базовые функции

Функция, которая определяет, как сильно форма кривой зависит от конкретной контрольной точки Вi, называется базовой функцией (basis function) этой контрольной точки.

Замечание

Собственно, в названии В-сплайнов буква "В" и означает "базовые" (basis).

Значение базовой функции представляет собой вещественное число. Необходимо учесть, что описание NURBS-кривой требует задания базовой функции для каждой контрольной точки.

Пример-метафора

Можно описать значения функции для выбранного значения параметра t, например, таким образом: 30% положения одной контрольной точки плюс 60% — другой и плюс 10% — третьей. Это, в частности, означает, что когда движущаяся частица удаляется от некоторой контрольной точки, она испытывает все меньшее воздействие. И наоборот, при приближении частицы к контрольной точке ее положение все больше от нее зависит. И такой эффект повторяется всякий раз, когда движущаяся частица проходит все контрольные точки.

Теперь следует сосредоточиться как раз на том, что подобное "влияние" контрольной точки может быть не только выражено числовыми значениями, но и визуализировано на графике (коль скоро это тоже функция). Таким образом, можно построить график базовой функции как зависимость влияния на движущуюся частицу, например в процентах, от значения 1(рис. 12.9).

Максимальный эффект (максимальное влияние) достигается в совершенно определенной точке и постепенно уменьшается по мере удаления. Форма кривой, описывающей эту зависимость, напоминает колокол.

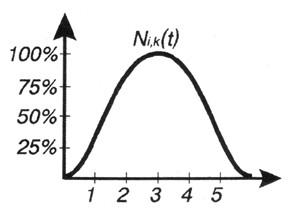
Рис. 12.9. Типичный график базовой функции отдельной контрольной точки

Поскольку каждая контрольная точка "обязана" иметь свою базовую функцию, NURBS-кривая, построенная, например, по пяти контрольным точкам, должна иметь пять таких функций, перекрывающих некоторую область результирующей кривой (рис. 12.10).

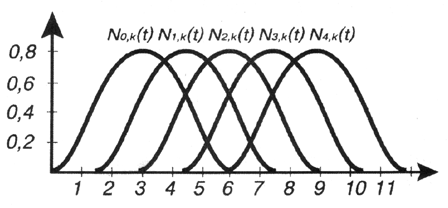
Рис. 12.10. Однородные базовые функции для множества контрольных точек

Узлы

На рис. 12.10 все базовые функции имеют одинаковую форму и размещены на равных расстояниях друг от друга. Это очень симметрично и элегантно, но на самом деле желательно варьировать длины интервалов таким образом, чтобы определенные контрольные точки влияли на значительно больший сегмент кривой, а определенные — на меньший. Это создает условие для неоднородности (Non-Uniform) в описании кривой.

Однако определение последовательности точек, на которые разбивается ось параметра t, является не очень легкой задачей. Ведь при изменении относительных интервалов между такими точками, вам представится возможность менять длительность воздействия контрольных точек на движущуюся вдоль кривой частицу.

Точки, разграничивающие интервалы, получили название узлов (knots), а их упорядоченный список — название узлового вектора (knot vector).

Узловой вектор базовой функции, представленный на рис. 12.11, имеет вид {0.0, 1,0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}.

Это пример однородного узлового вектора (uniform knot vector), в котором все функции определены на одинаковых временных интервалах.

Рис. 12.11. Пример однородного узлового вектора

Следующий рисунок (рис. 12.12) представляет пример кривой, созданной на основе такого узлового вектора.

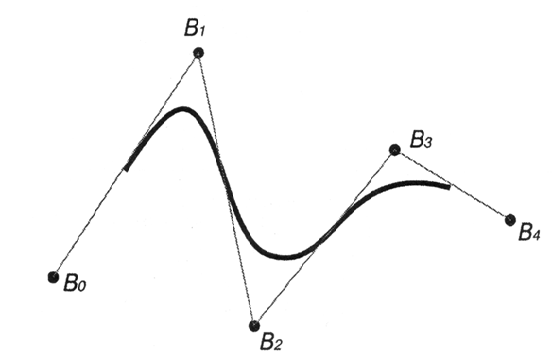
Рис. 12.12. NURBS-кривая с однородным узловым вектором

Если изменить узловой вектор, например, следующим образом: {0.0, 1.0, 2.0, 3.75, 4.0, 4.25, 6.0, 7.0}, то получится другое множество неоднородных (non-uniform) базовых функций (рис. 12.13) и, соответственно, другая форма кривой (рис. 12.14), которая строится на тех же контрольных точках, что и на рис. 12.12.

Рис. 12.13. Неоднородные базовые функции для множества контрольных точек

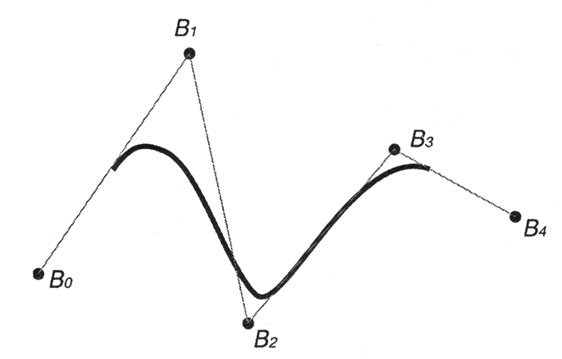
Рис. 12.14. NURBS-кривая с неоднородным узловым вектором

Характеристика семейства базовых функций

Для любого значения параметра t сумма всех базовых функций строго равна 1.

Если веса всех контрольных точек положительны, кривая лежит в области, полученной соединением крайних (внешних) контрольных точек. Такой "габаритный" контейнер получил название "выпуклой оболочки" (convex hull).

Рациональные кривые

Обратимся к ключевой букве в названии NURBS — "R", что означает "rational" (рациональный). Рациональные кривые, в сравнении с обычными (нерациональными — "non-rational") В-сплайнами, обладают двумя дополнительными и очень важными свойствами:

-они обеспечивают корректный результат при проекционных трансформациях (например, масштабировании), а нерациональные В-сплайны — только при аффинных трансформациях (например, перемещениях);

-их можно использовать для моделирования кривых любого вида, включая конические сечения (окружности, эллипсы, параболы и гиперболы).

Эти свойства (кстати, весьма значительные) достигаются за счет четырехмерного представления обычной трехмерной контрольной точки {х, у, z}. Это значит, что каждая контрольная точка представляется четырьмя координатами {х, у, z, w}. Последняя координата w означает вес (weight) контрольной точки, о котором уже упоминалось ранее (вспомним пример с гравитацией или холодильником).

Замечание

"Вес" в математическом смысле — это значение, важность, влияние, которое выражается особой функцией или числовым значением. Это одно из важных понятий в теории принятия решений.

Изначально координата w равняется единице, но при увеличении этого значения для контрольной точки увеличивается степень ее воздействия на форму кривой и последняя сильнее выгибается в сторону контрольной точки (рис. 12.15).

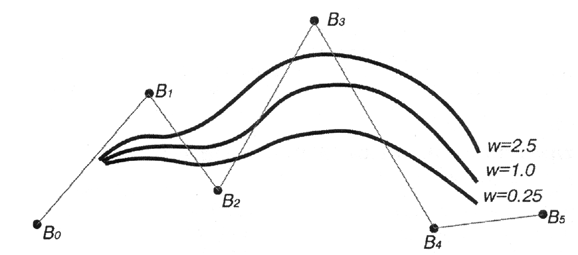
Рис. 12.15. Изменение формы кривой при изменении веса контрольной точки

Замечание

Важно заметить, что существенным является только относительное изменение весов контрольных точек. Если вдвое увеличить веса всех контрольных точек, то форма кривой не изменится.

Пример

Квадратичная (второй степени) NURBS-кривая определяется тремя контрольными точками (рис. 12.16). У всех трех кривых узловой вектор имеет вид {0.0, 0.0, 0.0, 1.0, 1.0, 1.0}. Веса первой и последней контрольных точек у каждой кривой равны 1. Если вес центральной вершины меньше 1, то результирующая кривая представляет собой сегмент эллипса (рис. 12.16, а). Если ее вес равняется 1, образуется парабола (рис. 12.16, б). Если же ее вес гораздо больше 1, то кривая преобразуется в гиперболу (рис. 12.16, в).

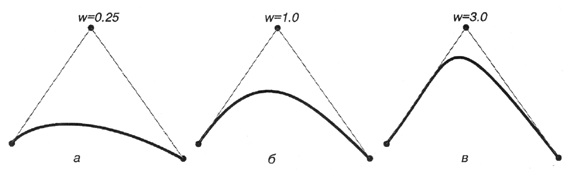
Рис. 12.16. NURBS-кривые с различными весами центральной контрольной точки

При всех своих непревзойденных свойствах NURBS-кривые все же обладают следующим громадным недостатком: расширенные возможности не могли не сказаться на уровне и сложности инструментария для их построения, а это, в свою очередь, требует от дизайнера повышенных условий для освоения, не говоря уже о необходимости определенного уровня математической подготовки (иначе трудно ожидать, что удастся разобраться во всех преимуществах и получить творческую свободу).

Кривая Безье (формулы и принципы построения)

В общем случае кривая Безье — это частный случай В-СПЛАЙНОВ (NURBS-кривых), которые можно определить как взвешенная сумма n+1 контрольных точек, где весовыми коэффициентами являются полиномы Бернштейна. Рассмотрим определения первых трех степеней кривой Безье.

Линейная кривая, кривая первой степени (прямая), определяется следующей параметрической формулой:

P(t) = (1 - t)P₀+tP₁

Это выражение представляет собой линейную интерполяцию между двумя точками (рис. 12.17).

Рис. 12.17. Кривая первой степени (прямая)

Квадратичная кривая, кривая второй степени, определяется формулой:

= (1 - t)²P₀ + 2(1 - t)tP₁ + t²P₂.

Это выражение представляет собой линейную интерполяцию между линейными интерполяциями между точками (рис. 12.18):

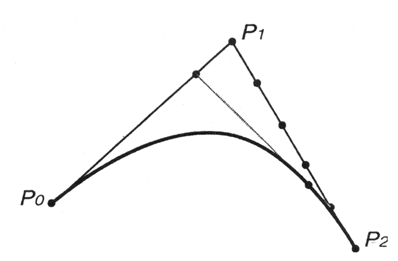
Рис. 12.18. Кривая второй степени (квадратическая кривая)

Кубическая кривая, кривая третьей степени, определяется формулой:

P(t) = (1 - t)³Р₀ + 3(1 - t)²tP₁ + 3(1 - t)t²P₂ + t³Р₃.

Это выражение представляет собой линейную интерполяцию между линейными интерполяциями между линейными интерполяциями между точками (рис. 12.19).

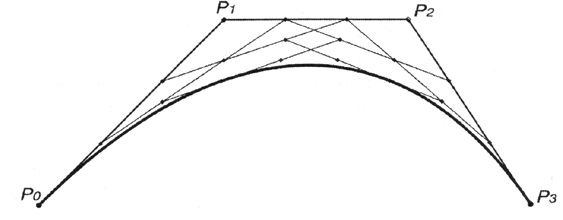
Рис. 12.19. Кривая третьей степени (кубическая кривая)

Свойства кривых Безье

Кривые Безье любой степени обладают следующими важными свойствами. Начальная и конечная контрольные точки лежат на кривой.

Кривая на всем протяжении непрерывна, у нее отсутствуют разрывы. Это важнейшее свойство, без которого кривая Безье вообще бы не рассматривалась.

Касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с другими двумя соседними контрольными точками, через которые в общем случае кривая не проходит.

Точки на краях касательных будут располагаться на кривой только в том случае, если последняя представляет собой прямую линию.

Поскольку кривая Безье представляет собой взвешенное усреднение всех ее контрольных точек с положительными весами, а сумма их равна единице, кривая всегда располагается внутри выпуклого многоугольника из ее контрольных точек (рис. 12.20), как и рассмотренная выше NURBS-кривая.

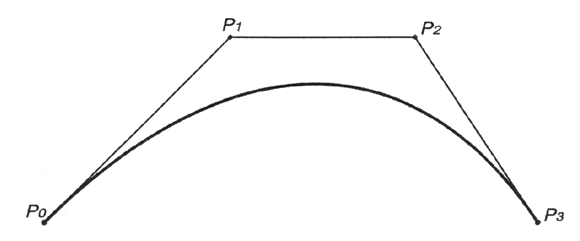
Рис. 12.20. Кривая в выпуклом многоугольнике

Кривую Безье можно рассматривать как пошаговое уточнение формы многоугольника, получаемого последовательным соединением ее контрольных точек (рис. 12.21—12.24). При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма определяется относительным расположением оставшихся точек, через которые в общем случае она не проходит.

Исходя из этого можно представить канонический вид кривой Безье, который обычно используется в графических редакторах плоской графики.

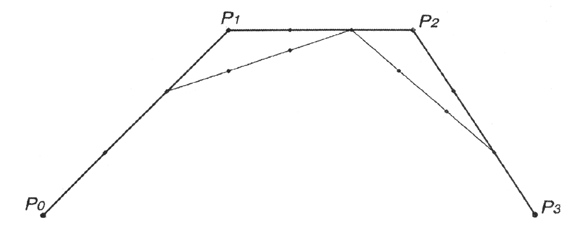
Рис. 12.21. Первый этап аппроксимации кривой

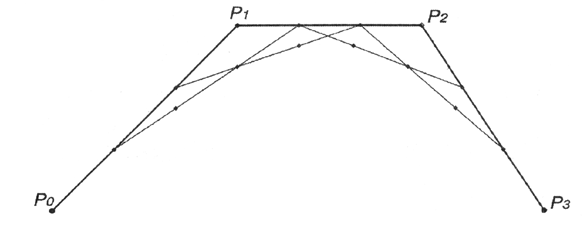
Рис. 12.22. Второй этап аппроксимации кривой

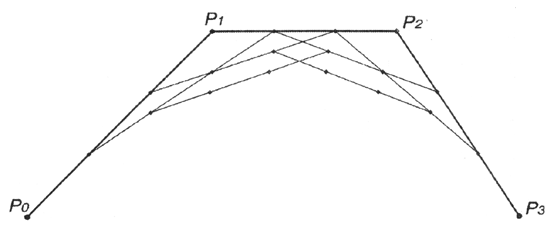
Рис. 12.23. Третий этап аппроксимации кривой

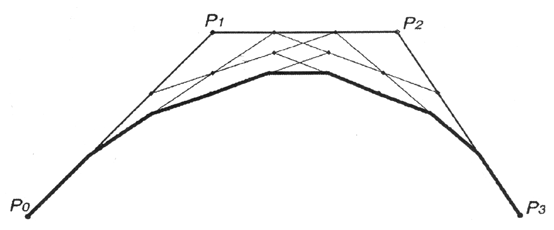
Рис. 12.24. Итоговая ломаная кривая

Канонический вид кривой Безье

Рассмотрим канонический вид кривой Безье и попытаемся понять, как из одной-единственной кривой получается бесконечно большое многообразие форм, которые используются в векторной компьютерной графике.

Общий вид кривой Безье имеет вот такую конструкцию (рис. 12.25).

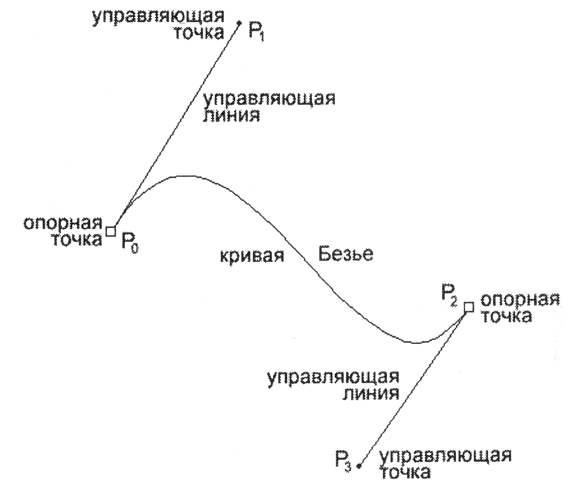
Рис. 12.25. Канонический вид кривой Безье

Причем, это уже не математическое описание, а сугубо прикладное отображение, именно то, которое знакомо всем пользователям векторных программ.

Замечание

Такое отображение все чаще используется и в программах пиксельной графики, а также в программах верстки.

Для построения этой кривой требуются четыре контрольные точки. Но кривая физически проходит только через две из них, они получили название опорных. Одна из точек называется начальной (start point), а другая — конечной (end point). Две точки остаются в стороне, они получили название управляющих (control point).

И для того чтобы их не "потерять" (особенно когда в документе кривых насчитываются многие десятки и сотни), в программах векторной графики, да и в любых других программах, управляющие точки соединяются с опорными точками какой-нибудь линией. Иногда пунктирной, иногда тонкой сплошной.

Почему кривая располагает начальной и конечной точками? Потому что, вообще говоря, кривая Безье — это, прежде всего, вектор.

Справка

Слово "вектор" латинского происхождения: "vector" переводится как "несущий", в математике используется для обозначения отрезка определенной длины и направления. Два вектора считаются равными лишь в том случае, если у них не только одинаковы длины, но и совпадают направления (то есть они параллельны и одинаково ориентированы). При изменении направления меняется знак вектора. В естественных науках векторы изображают величины, которые имеют направление, например сила, скорость, ускорение и т. д.

Направление кривой, может быть, не всегда очевидно для пользователей векторной программы, но для самой программы оно всегда существенно. Направление контуров находит свою реализацию в так называемых составных контурах (compound paths). Если два векторных объекта, например образующих букву "о" и расположенных друг на друге, направлены в противоположные стороны (рис. 12.26), то изображение получится "с дыркой посередине".

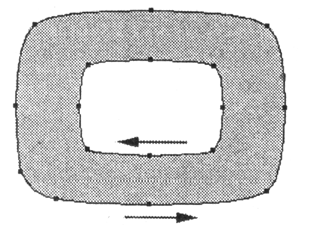
Рис. 12.26. Составной контур с разнонаправленными векторами

Если те же векторные контуры направлены в одну сторону, то в этом случае один контур просто перекрывает другой, не образуя прозрачной области (рис. 12.27).

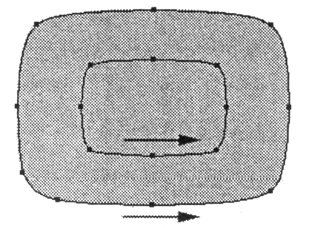
Рис. 12.27. Составной контур с однонаправленными векторами

Изменение формы кривой

Как же изменить форму канонической кривой Безье, чтобы с ее помощью получить огромное многообразие форм, из которых можно составить объект любой сложности?

В программах векторной графики существует единственный способ — это интерактивное перемещение опорных и управляющих точек. Если перемещаются начальная или конечная точки, то кривая станет соответствующим образом изменяться (вытягиваться или сжиматься как упругая резинка). Перемещение управляющих точек изменяет кривизну соответствующей "половинки" кривой Безье, входящей в начальную или конечную точки (рис. 12.28).

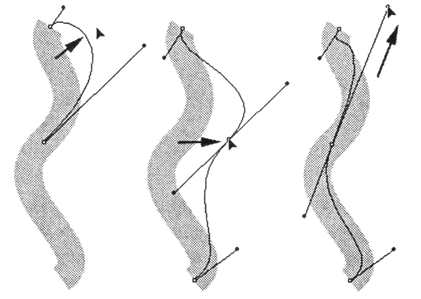
Рис. 12.28. Способы изменения формы сегмента

Таким образом, с помощью перемещения этих четырех точек получают неограниченное количество форм кривой Безье, которая может быть всего-навсего одним отдельным сегментом сложного секторного контура.

Разумеется, векторные редакторы позволяют работать одновременно с несколькими опорными точками (перемещать, вращать и т. п.).

Соединение нескольких секторов

Теперь необходимо рассмотреть, как создается многообразие контуров с помощью соединения нескольких канонических кривых Безье в связанную последовательность, часто даже замкнутую (рис. 12.29).

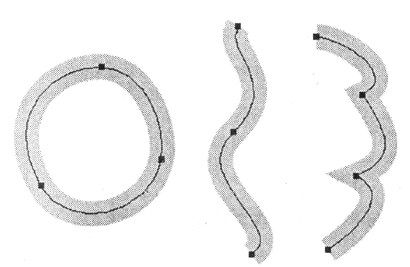
Рис. 12.29. Примеры векторных контуров, составленных из кривых Безье

В каждом сегменте можно добавлять опорные точки, в данном случае появляются две дополнительные управляющие точки с управляющими линиями, которые тоже позволяют изменять форму кривой. Добавление новых опорных точек в пределах одного сегмента кривой не противоречит тому условию, что отдельные кривые соединяются в цепь. Просто кривая Безье добавляется не к концу контура, а размещается внутри уже имеющегося контура.

Замечание

Для того чтобы отличать кривую как элементарную кривую, исходную кривую и кривую, которая уже находится в составе контура, последнюю чаще всего принято называть сегментом (сегментом контура или сегментом кривой).

По сути дела любая векторная конструкция (векторный контур или векторная форма) создается из векторных сегментов, каждый из которых идентичен отдельной элементарной кривой Безье.

Отсюда следует, что между ними образуются соединительные точки, которые иногда называются узлами (например, nodes — в графическом редакторе CorelDRAW). Метафора в этом случае очевидна: куски проволоки связываются узелками.

В других программах эти точки называются опорные точки (anchor point), дословно "якорные точки" (Adobe Illustrator), или просто точки (Macromedia FreeHand).

Для поддержки соотношения между элементарными сегментами существуют разные типы опорных точек.

Типы опорных точек

Соединительные точки между сегментами бывают нескольких типов. Действительно, можно предположить, что в одном случае требуется обеспечить соединение, скажем, криволинейного сегмента с прямым, в другом случае получить идеально гладкое сочленение (сопряжение), т. е. без стыка или перегиба.

В качестве образцов опорных точек составим таблицу для следующих векторных программ, использующих кривые Безье: CorelDRAW, Adobe Illustrator и Macromedia FreeHand.

Замечание

Типы опорных точек в трехмерной графике представлены ниже на примере Autodesk 3D МАХ.

Первый тип опорной точки, который соединяет два сегмента, обеспечивает независимость управляющих точек по направлению и длине друг от друга.

Такое состояние сегментов называется изгиб (рис. 12.30).

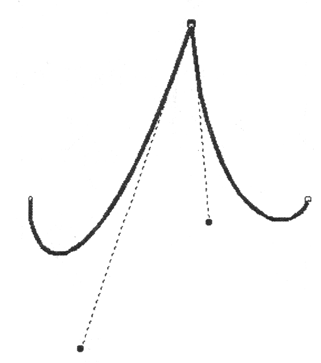
Рис. 12.30. Пример точки перегиба

В программе CorelDRAW такая точка называется перегиб (cusp). В других программах у нее более простое имя: угловая (corner). Помимо этого, в программе FreeHand при выделении угловая точка обозначается квадратиком.

Угловое сочленение сегментов (изгиб) далеко не всегда разумно и выгодно. Например, для создания окружности необходимо обеспечить соединение, которое в черчении и в геометрии называют гладким сопряжением, когда одна кривая плавно переходит в другую. Такое сочленение обеспечивает гладкая опорная точка (smooth) (рис. 12.31).

Условием этого являются управляющие линии, лежащие на одной прямой. У такой точки направление управляющих линий фиксировано относительно друг друга, при перемещении одной управляющей линии другая также движется синхронно как рычаг. Вместе с тем, такие управляющие линии могут различаться по величине.

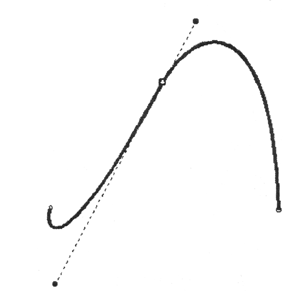
Рис. 12.31. Пример гладкой точки

У программы CorelDRAW предусмотрен подвид гладкого сочленения, который называется симметричный узел (symm от слова "symmetrical") (рис. 12.32). Суть его состоит в том, что управляющие линии фиксируют не только по направлению, но и по величине (длина направляющих всегда одинакова). Если одну из них увеличивать или уменьшать, другая будет синхронно повторять это действие.

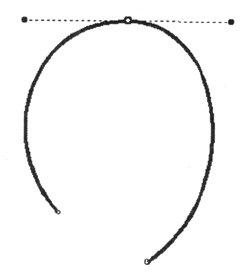
Рис. 12.32. Симметричная опорная точка

Замечание

В программах Adobe Illustrator и Macromedia Freehand такой тип опорной точки отсутствует, хотя его можно получить вручную.

В свою очередь, у программы FreeHand в отдельный вид опорных точек выделен случай гладкого сочленения прямолинейного и криволинейного сегментов (рис. 12.33). Такая точка получила название тангенциальной (connecter point). При выделении такая точка обозначается треугольником.

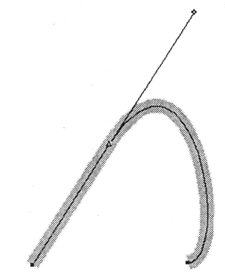
Рис. 12.33. Пример тангенциальной точки в программе FreeHand

Логика этой точки заключается в следующем: для того чтобы криволинейный сегмент гладко сопрягался с прямой линией, касательная криволинейного сегмента должна совпасть с продолжением прямого сегмента. Поэтому управляющая точка криволинейного сегмента способна двигаться только вдоль этой касательной.

Замечание

В программах CorelDRAW и Adobe Illustrator такое соединение также имеет место, но не выделено в специальный тип опорной точки.

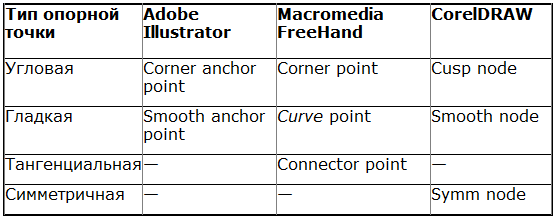
Типы опорных точек можно суммировать в виде следующей таблицы (табл. 12.1).

Таблица 12.1. Типы опорных точек в различных векторных программах

Типы опорных точек в трехмерной графике имеют ту же основу, но отличаются другими характеристиками (в качестве примера можно рассмотреть опорные точки в программе Autodesk 3D МАХ).

Smooth (гладкая): вершина, через которую кривая проходит "неуправляемо" гладко. Форма кривой определяется расстоянием между соседними вершинами.

Corner (угловая): вершина, в которой кривая получает излом.

Bezier (Безье): вершина Безье с управляющими рычагами, которые не равны по длине, но ориентированы строго в противоположных направлениях. Форма кривой зависит и от направления касательных, и от длины рычагов.

Bezier Corner (угловая Безье): все характеристики идентичны опорной точке Bezier, но угол между управляющими рычагами может быть произвольным, т. е. допускается излом на кривой.

Язык PostScript

ЯЗЫК описания страницы PostScript был создан в начале 80-х годов прошлого века фирмой Adobe. Его идеология состояла в том, что он был призван стать языком управления графическим устройством, например лазерным принтером, а не просто выполнять узкую задачу — позиционировать только черные точки, т. е. не только создавать битовую карту изображения с учетом разрешения выводного устройства (так работает язык PCL). Главная обязанность этого языка должна заключаться в передаче информации между прикладными программами (графическими редакторами, программами верстки) и устройствами визуализации (лазерными принтерами, фотонаборными автоматами и цифровыми офсетными машинами).

Поэтому формирование полной битовой карты страницы было перенесено в обязанность принтера, что вызвало необходимость включить в его состав как вычислительный блок, так и блок памяти.

В основу языка были положены следующие условия.

Основой векторного принципа кодирования графической информации приняты кривые третьего порядка (кривые Безье). И что очень важно, эти кривые использовались для описания как графики, так и шрифта, что обусловило единые алгоритмы обработки (с некоторыми небольшими отличиями).

С самого начала было принято решение разрабатывать PostScript как язык программирования высокого уровня, а не просто язык линейного управления внешним печатающим устройством. Поэтому были предусмотрены все возможности, свойственные классическим языкам программирования, например циклы, ветвления, подпрограммы и т. д. Кроме того, очень важно отметить, что PostScript это язык интерпретирующего типа (программа обрабатывается по мере поступления команд). Файлы в формате PostScript сохраняются в виде обычных текстовых символов (первая половина кодовой таблицы ASCII), что позволяет "рисовать" страницы в обычном текстовом редакторе, сейчас, конечно, это не имеет значения, но в свое время впечатляло. Поэтому, в сущности, документ, написанный на языке PostScript или сгенерированный из какого-либо приложения, — это программа, которая подлежит выполнению, и этим "занимается" интерпретатор языка, входящий в состав принтера. Такая программа может быть совсем короткой, и ее передача на принтер займет не так много времени (чего, впрочем, нельзя сказать о ее выполнении), а может быть и очень значительной и ее передача на принтер может происходить не один час.

Изображение, которое описывается с использованием языка PostScript, никаким образом не связано с разрешающей способностью конкретных устройств вывода. Процесс приспособления изображения к возможностям принтера (процессы растеризации и растрирования) происходит уже в самом принтере, тем самым добивается максимальное качество, на которое он способен. Заранее готовить изображение, приспособленное к конкретному принтеру, нет необходимости.

С точки зрения содержания язык PostScrip — это графика, основанная на кривых Безье. Кривые Безье — это воображаемые линии, которым можно присвоить обводку (stroke) и заливку (fill). Кроме того, возможны импортирование и обработка пиксельной графики.

Эти условия и их реализация вывели язык PostScript на позиции несомненного лидера и позволили ему стать основой всей области компьютерной графики и полиграфии.

Последующее развитие языка не изменило своей основы, но шло по пути интегрирования новых возможностей выводных устройств (цветная печать, систем управления цветом и т. д.).