Гладкие кривые

Все умные места кривые.

Мераб Мамардашвили

Одной из самых важных причин выбора в качестве средств векторной графики кривых Безье и NURBS-кривых является управляемая гладкость. Гладкость означает, что при моделировании на кривой не образуется петель и резких преломлений (тем более разрывов). Но при этом, не исключена возможность создания как гладкого сопряжения, так и изгибов, например острых углов.

Прекрасным примером такого сочетания гладких кривых и острых преломлений являются профили авиакрыла. Обсудим гладкость кривых.

Пример-метафора

Продолжая метафору частицы, перемещающейся по кривой, можно сказать, что у нее на пути вдоль параметрической кривой не должно быть остановок (кроме начала и конца) и внезапного изменения направления.

Для того чтобы представить направление движения частицы, можно мысленно "укрепить" на ней стрелку, которая непрерывно указывает направление движения вдоль параметрической кривой.

На математическом языке стрелка на частице называется касательной. Если касательная в соседних точках не меняет внезапно своего направления, такую кривую считают гладкой (рис. 12.4).

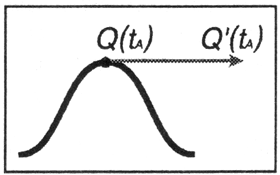
Рис. 12.4. Касательная на гладкой кривой

Если «на кривой имеется излом, то направление касательной в точке Q меняется практически мгновенно (рис. 12.5).

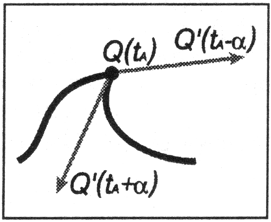
Рис. 12.5. Касательная на кривой с изломом

Теперь мы должны подробнее познакомиться с основами построения гладких кривых, применяющихся в векторной компьютерной графике. Начнем с NURBS-кривых, которые являются более общим (а соответственно, и более сложным) случаем таких кривых.

NURBS-кривая

Обсуждение стоит начать с объяснения термина NURBS, который является аббревиатурой (сокращением) и расшифровывается как Non-Uniform Rational B-spline, где:

"Non-Uniform" (неоднородный) означает, что область влияния контрольной точки на форму кривой может быть различной. Это очень важное свойство для моделирования иррегулярных кривых.

"Rational" (рациональный) означает, что математическое выражение, описывающее форму моделируемой кривой, есть отношение двух полиномов.

Эта особенность позволяет точнее моделировать различные кривые, например, конические сечения.

"B-spline" (basis spline, базовый сплайн) — способ математического описания кривой интерполяцией между тремя и более контрольными точками.

Замечание

Кривые Безье являются специальным (частным) случаем В-сплайна.

Контрольные точки

Для начала вспомним, что в определении параметрической кривой левая часть выражения, описывающая функцию q, выглядит так:

q(t) = ...,

где t — параметр, представляющий заданный набор значений определенного диапазона, как правило, от 0 до 1. Используя эти значения, получают последовательность пар {х, у}, по которым строится моделируемая кривая (рис. 12.6).

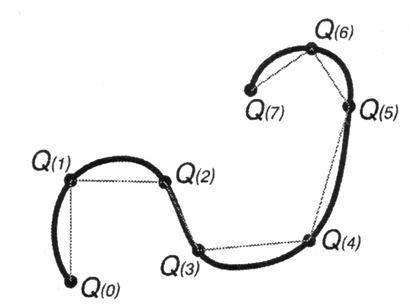
Рис. 12.6. Пример построения параметрической кривой

В указанном выше выражении не определена правая часть, т. е. собственно параметрическое уравнение, а точнее, параметрические уравнения.

Одной из основополагающих особенностей NURBS-кривой является то, что ее форма определяется расположением множества контрольных точек (control points). На рис. 12.7 эти точки обозначены как Bi.

Замечание

Контрольные точки соединены для наглядности прямыми линиями. Эта ломаная линия получила название управляющего многоугольника (control polygon).

Рис. 12.7. Множество контрольных точек, определяющих параметрическую кривую

Эта особенность NURBS-кривой важна, поскольку позволяет локализовать изменение формы кривой перемещением отдельных контрольных точек без изменения формы всей кривой в целом (рис. 12.8).

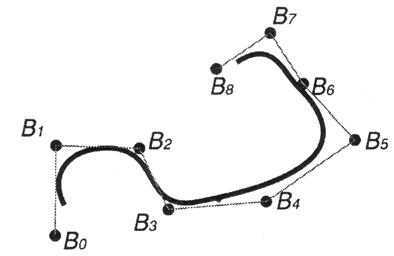
Рис. 12.8. Изменение формы фрагмента кривой, вызванное перемещением контрольной точки

Каждая контрольная точка определяет форму только той части кривой, которая находится в ее окрестности, и оказывает меньшее воздействие или вовсе не влияет на форму оставшейся части кривой.

Пример-метафора

В каждый данный момент положение движущейся частицы определяется как весовое усреднение положения всех контрольных точек. При этом контрольные точки, расположенные ближе к частице, оказывают большее влияние (как, например, большая масса небесного тела притягивает сильнее, поскольку сила гравитации у такого тела больше) при определении ее итогового положения в пространстве. Другими словами, для определения положения движущейся частицы необходимо просуммировать положение всех контрольных вершин (точек) с учетом меняющейся "значимости" (гравитации).

Если кому не очень ясен пример с гравитацией, можно предложить другую метафору. Выбор и покупка, скажем, холодильника определяются многими факторами (ценой, объемом, цветом и т. п.). Но эти факторы не равнозначны, каждый фактор имеет свою значимость, например цена важнее цвета, это значит, что у цены больший "вес" в сравнении с цветом. Если просуммировать "веса" всех факторов, то можно формально "вычислить", какой холодильник разумнее приобрести.