Преобразование дробей

В школе VIII вида учащиеся знакомятся со следующими преоб­разованиями дробей: выражением дроби в более крупных долях (6-й класс), выражением неправильной дроби целым или смешан­ным числом (6-й класс), выражением дробей в одинаковых долях (7-й класс), выражением смешанного числа неправильной дробью (7-й класс).

300

Выражение неправильной дроби целым или смешанным числом

Изучение данного материала следует начать с задания: взять 2 равных круга и каждый из них разделить на 4 равные доли, подсчи­тать количество четвертых долей (рис. 25). Далее предлагается

записать это количество дробью ( ) . Затем четвертые доли при­кладываются друг к другу и ученики убеждаются, что получился

целый круг. Следовательно, = 1. К четырем четвертям добавляет

ся последовательно еще по , и ученики записывают = 1, = 1 , = 1 , = 1 , = 2.

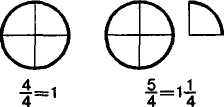
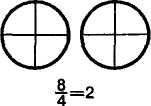
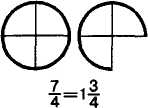
Рис. 25

Учитель обращает внимание учащихся на то, что во всех рас­смотренных случаях они брали неправильную дробь, а в результа­те преобразования получали или целое, или смешанное число, т. е. выражали неправильную дробь целым или смешанным чис­лом. Далее надо стремиться к тому, чтобы учащиеся самостоятель­но определили, каким арифметическим действием это преобразова- ние можно выполнить. Яркими примерами, приводящими к ответу

на вопрос, являются:

= 1, = 2 , = 1 , = 1 .

Вывод: чтобы выразить неправильную дробь целым или смешанным числом, нужно числитель дроби разделить на знаменатель, частное запи­сать целым числом, остаток записать в числитель, а знаменатель оставить тот же. Так как правило громоздкое, совсем не обяза­тельно, чтобы учащиеся заучивали его наизусть. Они должны уметь последовательно рассказать о действиях при выполнении данного преобразования.

Перед тем как познакомить учащихся с выражением непра­вильной дроби целым или смешанным числом, целесообразно по­вторить с ними деление целого числа на целое с остатком.

Закреплению нового для учащихся преобразования способству­ет решение задач жизненно-практического характера, например:

301

«В вазе лежит девять четвертых долей апельсина. Сколько целых апельсинов можно сложить из этих долей? Сколько четвер­тых долей останется?»

«Для изготовления крышек для коробочек каждый лист картона

разрезают на 16 равных долей. Получили . Сколько целых листов картона разрезали? Сколько шестнадцатых долей отрезали от следующего куска?» И т. д.

Выражение целого и смешанного числа неправильной дробью

Знакомству учащихся с этим новым преобразованием должно предшествовать решение задач, например:

«2 равных по длине куска ткани, имеющих форму квадрата, разрезали на 4 равные части. Из каждой такой части сшили

платок. Сколько получилось платков?» ( Запись: 2= , 2= ).

Далее учитель предлагает учащимся выполнить такое задание: «Возьмите целый круг и еще половину круга, равного по разме­ру первому. Разрежьте целый круг пополам. Сколько всего поло-

вин получилось? Запишите: было 1 круга, стало круга, значит, 1 = .

Таким образом, опираясь на наглядно-практическую основу, рассматриваем еще ряд примеров. В рассматриваемых примерах учащимся предлагается сравнить исходное число (смешанное или целое) и число, которое получилось после преобразования (непра­вильная дробь).

Чтобы познакомить учеников с правилом выражения целого и смешанного числа неправильной дробью, надо привлечь их внима­ние к сравнению знаменателей смешанного числа и неправильной

дроби, а также к тому, как получается числитель, например:

1 = ?, 1 = , да еще , всего ; 3 =?, 3= , да еще , всего будет . В итоге формулируется правило: чтобы смешанное число выразить неправильной дробью, надо знаменатель умножить на целое число, прибавить к произведению числитель и сумму запи­сать числителем, а знаменатель оставить без изменения.

Вначале нужно упражнять учащихся в выражении неправиль­ной дробью единицы, затем любого другого целого числа с указа­нием знаменателя, а уже затем смешанного числа:

302