44

МЕТРОЛОГИЯ

Единообразие средств измерении (СИ) – это такое состояние, когда все СИ проградуированы в узаконенных единицах, и погрешности СИ соответствуют нормам.

2. Научная или фундаментальная метрология – разрабатываются новые методы и СИ.

3. Практическая метрология – осуществляет непосредственное измерение физических величин (ФВ) с помощью СИ, их поверку, калибровку.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА КАК ОБЪЕКТ ИЗУЧЕНИЯ

ФВ – одно из свойств физического объекта, которая является общим для многих объектов в качественном отношении, но в количественном отношении индивидуально для каждого.

Истинное значение ФВ идеальным образом отражает в качественном и количественном отношениях соответствующее свойство объекта.

Нахождение истинного значения ФВ – это центральная проблема метрологии. Т.к. истинное значение ФВ определить невозможно, то на практике оперируют действительным значением в виде среднего, которое очень близко к истинному (при многократных измерениях одного и того же параметра).

Различают измеряемую ФВ, т.е. ту, которая подлежит измерению, и влияющую, т.е. ФВ, которая не измеряется СИ, но оказывает влияние на СИ или объект измерений.

Количественной характеристикой измеряемой величины служит ее размер. Получение информации о размере ФВ является содержанием любого измерения.

Шкала ФВ – упорядоченная последовательность значений ФВ, принятая по соглашению на основании результата измерений.

1) шкала наименований – основана на приписывании качественным свойствам объектов чисел, играющая роль имен. Эти числа нельзя использовать в математических операциях (атлас цветов)

2) шкала порядка – образована расположенными в порядке возрастания или убывания размерами измеряемых величин. Простейший способ получения информации о размере измеряемой величины с помощью шкалы порядка заключается в сравнении его с другим размером по принципу «больше или меньше», «лучше или хуже». Операция расстановки размеров в порядке их возрастания или убывания с целью получения измерительной информации по шкале порядка называется ранжированием. Для обеспечения измерений по шкале порядка некоторые точки на ней можно зафиксировать в качестве опорных (реперных) (шкала силы ветра – Бофорда, шкала для измерения вязкости Энглера, двенадцатибальная шкала Ритхера, шкала Мооса)

Недостатком реперных шкал является неопределенность интервалов между реперными точками.

3) шкала интервалов – разбита на крупные и мелкие интервалы. По ней можно судить не только о том, что один размер больше или меньше другого, но и о том, на сколько он больше или меньше. Однако при шкале интервалов невозможно оценить, во сколько раз один размер больше или меньше другого, т.к. известен только масштаб, а начало отсчета выбирается произвольно (шкала времени, температурные шкалы)

Шкалу интервалов величины Q можно представить уравнением

,

где Q₀ – начало отсчета шкалы; q – числовое значение величины; [Q] – единица рассматриваемой величины ; Q и Q₀ – опорные точки, просто реализуемые физически; n – целое число.

4) шкала отношений – шкала интервалов с естественным началом отсчета, которое соответствует полному отсутствию измеряемого признака. Она является наиболее совершенной. По ней можно судить, во сколько один размер больше или меньше другого. . Шкала Кельвина, шкала измерения массы.

5) абсолютная шкала – соответствует относительным единицам (коэффициентам). Такие шкалы характеризуются свойствами шкал отношений, но дополнительно имеют естественные однозначные единицы измерения, независящие от принятой системы единиц ФВ.

СИСТЕМЫ ЕДИНИЦ ФИЗИЧЕСКИХ ВЕЛИЧИН

Система единиц ФВ – совокупность основных и производных единиц, связанных между собой определенной зависимостью.

ПРИНЦИПЫ ПОСТРОЕНИЯ СИСТЕМЫ ЕДИНИЦ

1. основные единицы выбираются произвольно и независимо друг от друга. Их число минимально, но достаточно для образования всех производных единиц.

2. размер основных единиц должен быть удобен для практических целей.

3. все основные единицы обязательно должны иметь эталоны для хранения и воспроизведения этих единиц.

Система СИ состоит из следующих единиц измерения:

1) семь основных

2) свыше ста производных единиц

2.1) пятнадцать образованы из основных единиц (скорость, объем)

2.2) имеют специальные названия по фамилиям ученых (паскаль, ньютон)

2.3) две безразмерные произвольные единицы (до 1955 г. они назывались дополнительные) – единица измерения плоского угла – радианы, и телесного угла – стерадиан.

2.4) когерентные производные единицы, т.е. связан с другими единицами СИ уравнением, в котором числовой коэффициент принят равным единице (скорость).

3) внесистемные единицы

3.1) десять допускаются к применению наравне с единицами СИ

(масса – тонна и атомные единицы массы; время – сутки, угол – градус; минута, секунда град; объем – литры; длина – астрономические единицы, световая гора, парсеки; оптическая сила – диоптрии; площадь – гектары; энергия – электронные вольты, полная мощность – ар.)

3.2) временно допускаемые к применению (масса – карат (200 мг); длина – морские мили (1,852 км); давление – бар (10⁵ Па); скорость – узлы (0,514 м/с)).

Эти единицы подлежат отмене.

3.3) изъятые из употребления (лошадиные силы 1 л.с. – 735,499 Вт; миллиметры ртутного столба).

4) кратные и дольные единицы

Кратные – в целое число раз больше,

Дольные – в целое число раз меньше.

К ним существуют соответствующие приставки.

Достоинства СИ:

1) охвачены все единицы измерения в области науки

2) проведена унификация единиц ФВ

3) основные производные единицы имеют удобные размеры для использования.

Виды измерений

1. Прямые многократные измерения – измерения, при которых значение измеряемой ФВ может быть определено непосредственно из опытных данных.

2. Косвенные – при них измеряемую ФВ определяют на основании известной зависимости между этой величиной и величинами, значения которых получены при помощи прямого измерения.

3. Совокупные измерения – при них числовые значения измеряемой ФВ определяются решением системы уравнений. Эти уравнения получаются из совокупности зависимостей. Найденных при измерении одноименных величин в различных сочетаниях.

4. Совместные измерения – предусматривают одноименные измерения двух или нескольких неодноименных величин с целью отыскания зависимости между ними.

5. Прямые однократные измерения. Однократные измерения более характерны для производственных процессов, многократные производятся в лабораторных и исследовательских целях. Однократные измерения производят, если:

- при измерении происходит разрушение объекта измерений;

- нет возможности повторного измерения;

- имеет место экономическая целесообразность.

Однократные измерения возможны при следующих условиях:

- объем априорной информации об объекте измерений достаточен;

- модель объекта и измеряемый параметр не вызывают сомнений;

- изучен метод измерений, возможности погрешности устранены;

- метрологические характеристики СИ соответствуют нормам.

За результат прямого однократного измерения принимается измеренная величина. Доверительная вероятность принимается равной 0,95.

До измерения проводится априорная оценка составляющих погрешностей:

А) погрешность СИ, рассчитанная по метрологическим характеристикам

Б) субъективная личная погрешность оператора

В) погрешность метода измерений. Если две последние составляющие не превышают 15% основной погрешности СИ, то за погрешность результата принимают погрешность применяемого СИ.

В наиболее общем случае, когда влияющие величины соответствуют нормальным условиям, погрешность результата однократного измерения равна пределу основной погрешности СИ.

Если условия измерения отличаются от нормальных, то следует определять и учитывать пределы дополнительной погрешности.

6. Абсолютные измерения – основаны на прямых измерениях величин или использовании физических констант. F = mg.

7. Относительные – измерение отношения величин к одноименной величине, выполняющую роль единицы.

8. Равноточные измерения – ряд измерений какой-либо ФВ, выполненных одинаково по точности СИ в одних и тех же условиях.

9. Неравноточные измерения – ряд измерений какой-либо ФВ, выполненных различающимися по точности СИ и/или в разных условиях.

Методы измерений

Метод измерения – совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений (физическое явление или процесс, положенное в основу измерения).

1. Метод непосредственной оценки. Значения измеряемой величины определяют по отсчетному устройству прибора.

2. Метод сравнения с мерой. Измеряемую величину сравнивают с величиной воспроизводимой меры.

   1. Метод дополнения. Значение измеряемой величины дополняются мерой этой же величины с таким расчетом, чтобы на прибор сравнения действовала их сумма, равная заранее заданному значению.

   2. Метод замещения. Сравнение с мерой, в котором измеряемую величину замещают известной с помощью воспроизводимой меры

3. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной с помощью воспроизводимой меры. Метод позволяет получить результат высокой точности при использовании относительно грубых СИ.

Пример

L a x = ? x = L + a а – измеряемая величина

Действительное значение а_д будет отличаться от измеренного а на величину погрешности Δ.

L >> a, <<

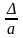
L = 1000 мм; а = 10 мм; Δ = 0,1 мм

% %

4. Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю. При этом метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины (мосты для измерения сопротивлений, неравноплечие весы). В общем случае совпадения сравниваемых величин регистрируют ноль-индикатором.

Кроме того, можно выделить нестандартизованные методы:

1. Метод противопоставления. Измеряемая величина и величина воспроизводимой меры одновременно воздействуют на прибор сравнения.

2. Метод совпадения. Разность между сравниваемыми величинами измеряют, используя совпадения отметок шкал или периодичность сигналов (измерение длины штангенциркулем).

Кроме того, если весь измеряемый параметр фиксируется непосредственно СИ, то это абсолютный метод, а если СИ фиксирует лишь отклонения параметра от установочного значения, то это относительный или пороговый между измерениями.