Раздел 4. Основы теории комплексных чисел

37. Какое числовое множество называют множеством комплексных чисел? Как это множество связано с остальными числовыми множествами? Какова геометрическая интерпретация комплексных чисел? Возможно ли на множестве решение квадратных уравнений с отрицательным дискриминантом?

38. Какая форма комплексного числа называется алгебраической? Какие операции можно выполнять над комплексными числами в алгебраической форме? Приведите примеры.

39. Какая форма комплексного числа называется тригонометрической? Что называют модулем и аргументом комплексного числа? Какие операции можно выполнять над комплексными числами в тригонометрической форме? Приведите примеры.

40. Какая форма комплексного числа называется показательной? Что называют модулем и аргументом комплексного числа? Какие операции можно выполнять над комплексными числами в показательной форме? Приведите примеры.

Задания для подготовки к экзамену

1. Вычислите определитель: а) ; б) ; в) .

2. Найдите матрицы А+В, 2А, 2А-3В, А·В, если А = , В = .

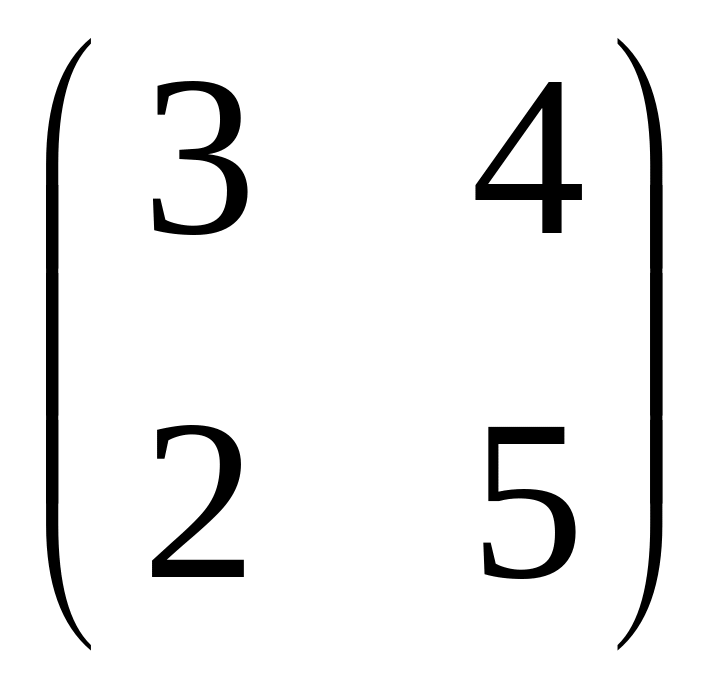3. Найдите матрицы, обратные данным: А = , В = .

4. Найдите ранг матрицы: а) ; б) .

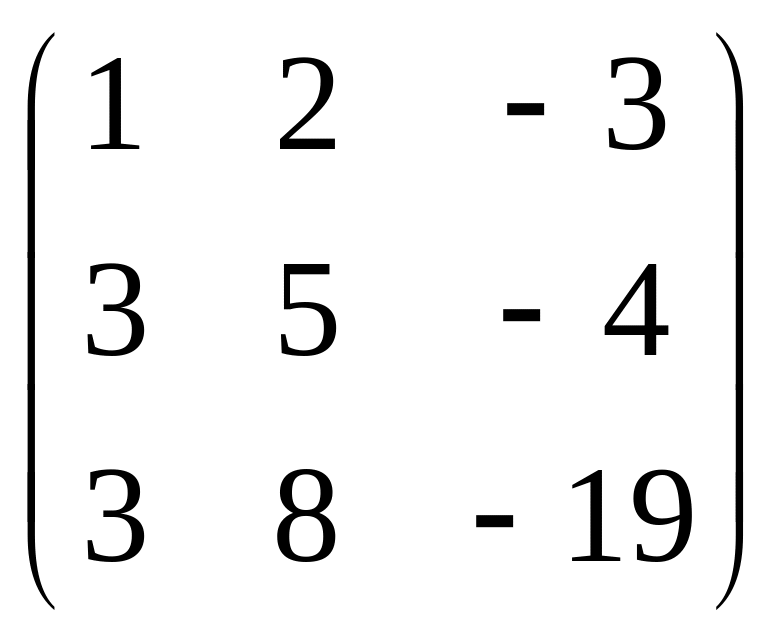5. Решите систему линейных уравнений по правилу Крамера и методом Гаусса:

а)

6. Известны координаты вершин треугольника: А(-3;2), В(2;-3), С(1;4). Составьте каноническое и параметрическое уравнение: а) сторон АВ и ВС, б) медианы ВМ, в) прямой, проходящей через точку В параллельно АС; г) прямой, проходящей через точку С, с угловым коэффициентом 5.

7. Постройте кривую второго порядка:

а) х²- =1; б) х²+ =1; в) (х–1)² + (у+4)² = 9; г) у=4х².

8. Вычислите предел: а) 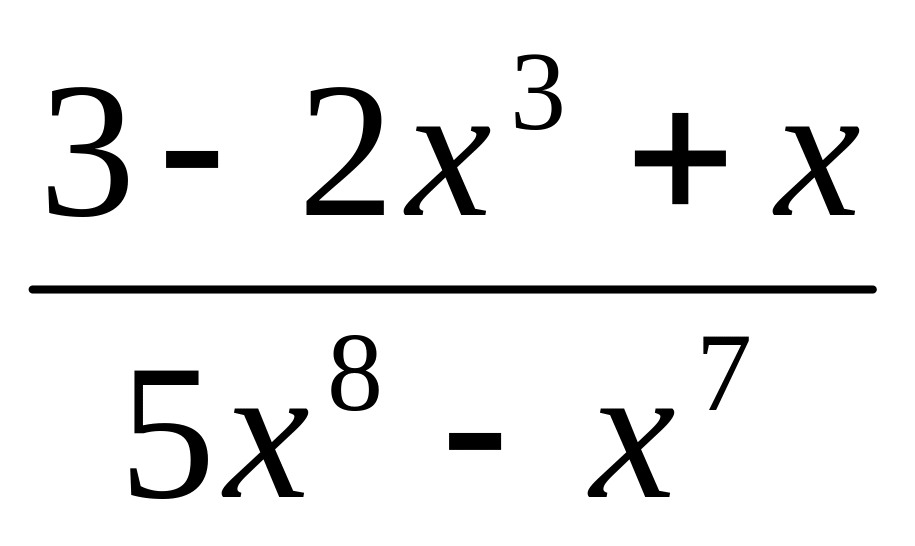; б) ; в) ;

г) ; д) ; е) .

9. Найдите точки разрыва функции и определите их род: а) у = , б) у = .

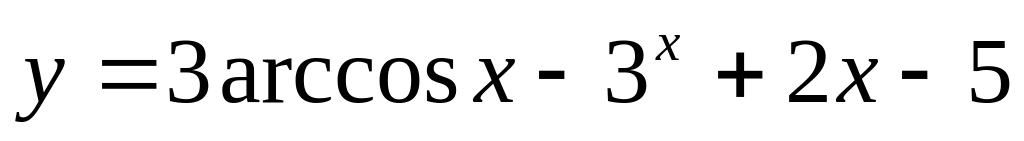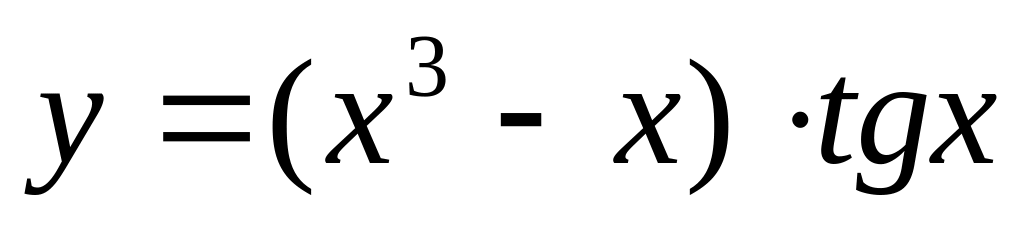10. Найдите производную функции: а) ; б) ; в) в точке х = 1; г) ; д) .

11. Найдите промежутки возрастания, убывания и экстремумы функции:

а) ; б) ; в) у = ; г) у = х – lnх.

12. Найдите промежутки выпуклости и вогнутости, точки перегиба графика функции:

а) у =х³ + 3х²; б) у = 3х⁴ - 8х³ + 6х; в) у = ln²х; г) у = х – lnх.

13. Найдите асимптоты графика функции: а) у = ; б) у = ; в) у = .

14. Найдите интегралы:

1) как интегралы от некоторых сложных функций: а) ; б) ;

в) ; г) ; д) ; е) ; ж) ;

2) методом подстановки: а) ; б) ; в) ; г) ; д) ;

3) методом по частям: а) ; б) ; в) .

15. Найдите площадь фигуры, ограниченной линиями: а) , , , ;

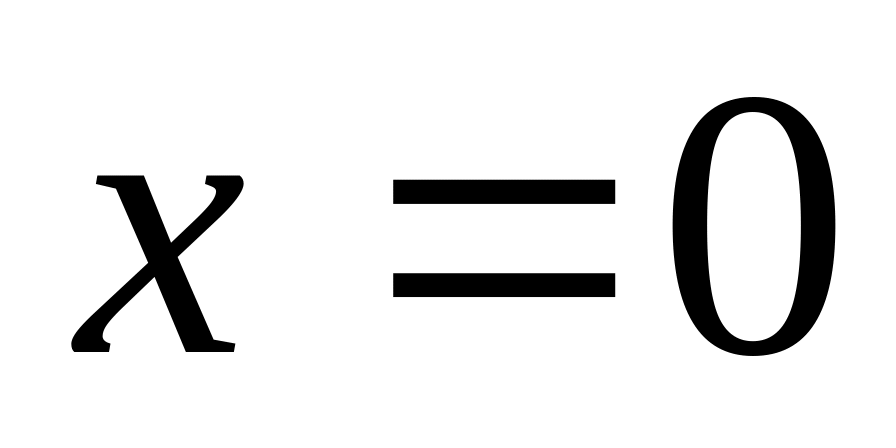б) , ; в) , , , , .

16. Найдите частные производные и дифференциалы первого и второго порядка для функций двух переменных: а) z=хсоsy+ y²; б) z=e^xarcsiny – 3^ylnx; в) z=x·y·e^x; г) z=сos(x³ – 4y²).

17. Вычислите двойные интегралы по прямоугольной области σ:

а) , где σ: 0≤х≤π/4, 1≤y≤2; б) , σ: 3≤х≤4, 1≤y≤е.

18. Вычислите двойной интеграл по произвольной области σ: х = 0, у = 0,

у = 3 – 3х.

19. Исследуйте на сходимость числовые положительные ряды с помощью

1. необходимого признака сходимости: а) ; б) ;

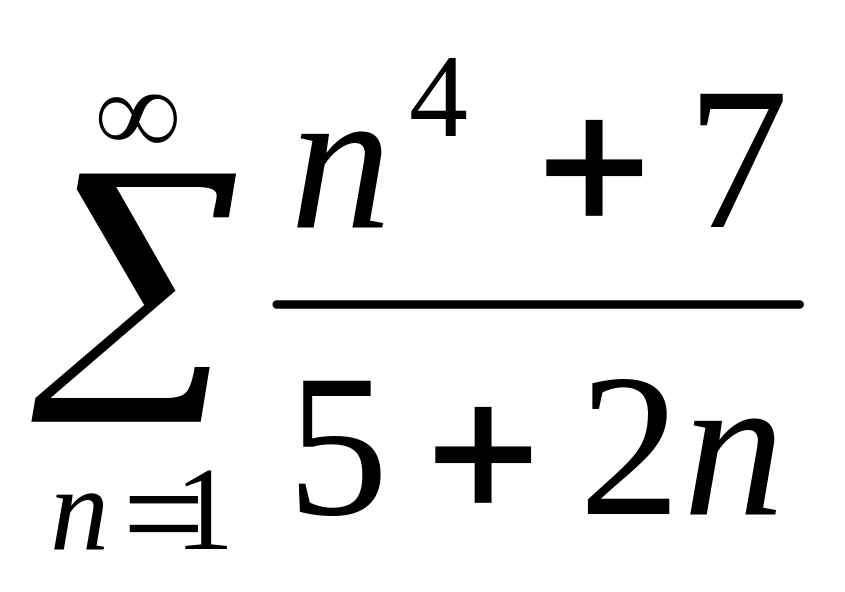2) признака сравнения (свойств рядов): а) ; б) ; в) ;

3) признака Даламбера: а) ; б) ; в) ; г) ;

4) признака Коши: а) ,б) .

20. Исследуйте на абсолютную и условную сходимость знакочередующиеся ряды:

а) ; б) .

21. Найдите радиус и интервал сходимости степенных рядов: а) ; б) .

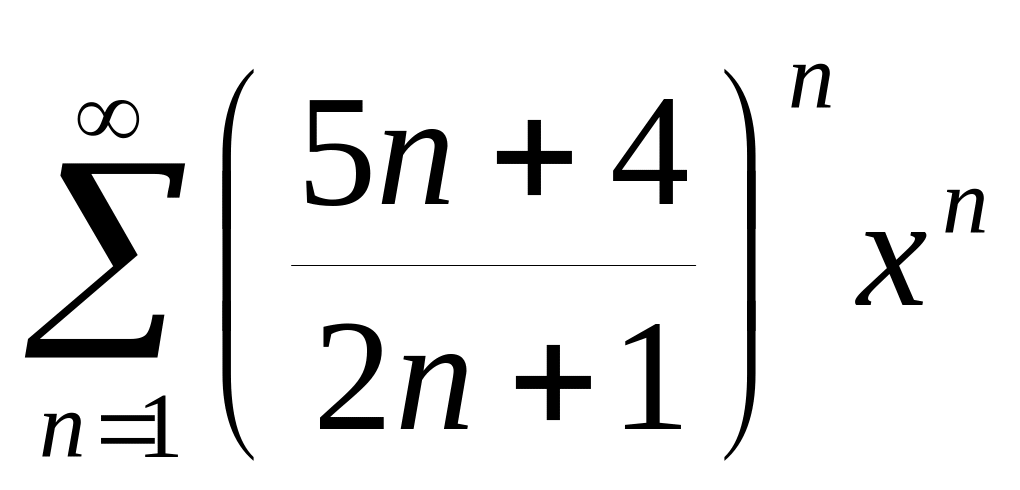22. Запишите разложения в ряд Маклорена для функций: а) у = е^4х; б) у = tgx; в) у = хе^6x.

23. Найдите решение дифференциальных уравнений:

1) простейших: а) у’ = , у(3)=2; б) у’ = е^3х + 1, у(0)=-3;

2) с разделяющимися переменными: а) у’ = х²у - х²; б) е^х(1 + е^у) + у’ е^у(1 + е^х) = 0;

3) однородных: а)(2х – 5у)dx + 3xdy = 0; б) (х² + ху + у²)dx - хуdy = 0;

4) линейных: а) у’ – 3у/х = -х/2; б) у’ + 2у = 4х; в) у’ - у = е^х;

5) простейших второго порядка: а) у’’ = 1/х²; б) у’’ = е^х - е^-х, у’(0) = 2, у (1) = 1/е;

6) линейных однородных второго порядка: а) у’’ - 10 у’ + 16у = 0; б) у’’ - 8 у’ + 16у = 0;

в) у’’ - 6 у’ + 10у = 0.

24. Представьте комплексное число в тригонометрической и показательной форме:

а) 3i; б) -1+ i; в) ; г) ; д) –5.

25. Представьте комплексное число в показательной и алгебраической форме:

а) ; б) .

26. Представьте комплексное число в тригонометрической и алгебраической форме:

а) ; б) .

27. Выполните действия: а) z₁₊ z₂, z_1· z₂, z_1:z₂, z₁², если z₁ = 3 – 8i, z₂ = -1 + 2i;

б) z_1· z₂, z_1:z₂, z₁⁴, , если z₁ = , z₂= ;

в) z_1· z₂, z_1:z₂, z₁⁶, , если z₁ = , z₂ = .

28. Решите уравнение: а) ; б) ; в) .