1. Определим неизвестные величины.

Неизвестными являются объемы перевозок.

Обозначим х_ij объем перевозок с i-й фабрики в j-й центр распределения, с_ij –соответствующая стоимость перевозки.

2. Определим целевую функцию Функция цели – это суммарные транспортные расходы, которые нужно минимизировать.

z =  с_ij х_ij

3. Установим ограничения модели.

-Объемы перевозок не могут быть отрицательными - х_ij>=0

-Так как условились рассматривать сбалансированную модель, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть удовлетворены. Обозначим а_i – объем производства на i-ой фабрике, b_j- спрос в j – м центре распределения. Ограничение для j-го центра - х_ij =b_j Ограничение для i-й фабрики - x_jj=a_i

Оформите решение задачи на листе EXCEL

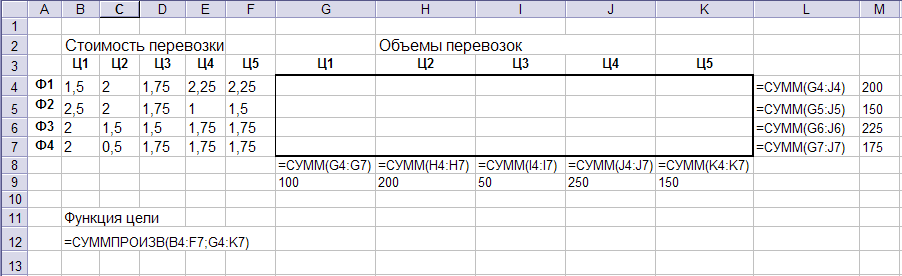
-Введите известные переменные - стоимость перевозок.

-Отведите блок ячеек под значения неизвестных – это объемы перевозок.

-Справа от блока неизвестных в ячейки введите формулы суммирования по строкам, для того чтобы сравнить эти суммы с заданными мощностями фабрик.

-Внизу блока неизвестных отдельно просуммируйте объем продукции, ввозимой в каждый центр распределения. Эти суммы также известны.

-Отведите ячейку под целевую функцию, для написания которой используйте функцию СУММПРОИЗВ.

Заполните диалоговое окно Поиск решения.

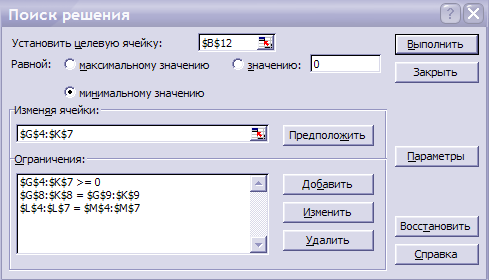
Установить целевую ячейку -

Равной - Минимальному значению.

Изменяя ячейки – неизвестными объемами перевозок.

Добавьте описанные выше ограничения:

-Ячейки с объемами перевозок больше или равны нулю.

-Ячейки, в которых будут суммироваться объемы продукции, вывозимой с фабрик равны ячейкам, в которых введены объемы производств на 4-х фабриках.

-Ячейки, в которых будет суммироваться объемы ввозимой продукции, равны ячейкам, в которых введена потребность продукции в 5 центрах распределения.

В Параметрах не забудьте установить флажок Линейная модель.

Нажмите кнопку Выполнить. Поиск решения рассчитает оптимальный план поставок продукции и соответствующие ему минимальные транспортные расходы.

Случай 2. Модель перевозок не сбалансирована. Это может проявиться либо в перепроизводстве, либо в дефиците продукции.

В случае перепроизводства продукции необходимо ввести фиктивный пункт потребления, стоимость перевозки единицы продукции в который будет равна стоимости складирования, а объемы перевозок – объемам складирования излишек продукции на фабриках.

В случае дефицита продукции необходимо ввести фиктивную фабрику. Стоимость перевозки едꗬÁ䀵Й15ዸ¿1515က1515؀15訂

߂161616퍪16IJ16騚161616騚16"16騼161616騼161616騼161616鬛161616鬛161616鬛161616퉽1616퉿161616퉿161616퉿161616퉿161616퉿161616퉿16$16풜16ɒ16훮16z16튣16161616161616161616ޮ161616鬛1616161616161616161616鬗1616鬛161616鬛161616鬛161616튣1616ктов потребления продукции. Стоимость перевозки единицы продукции из пункта производства в пункт распределения приведены в таблице (строка- пункт производства, столбец – пункт потребления). При этом, в конце каждой строки указан объем производства в соответствующем пункте производства, а внизу каждого столбца указан спрос в пункте распределения.

Нужно составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.