6. Задача о назначениях

Четверо рабочих могут выполнять четыре вида работ. Стоимость выполнения i-м рабочим j-й работы приведены в таблице:

Рабочие	Виды работ
	1	2	3	4
1	1	4	6	3
2	9	10	7	9
3	4	5	11	7
4	8	7	8	5

Необходимо составить план выполнения работ так, чтобы все виды работ были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполненных работ была минимальной.

Решение.

1. Определим переменные для построения математической модели задачи. Стоимость выполнения j-ой работы i- м рабочим обозначим C_ij Введем переменную X_ij, которая равна 1, если i-й рабочий выполняет j-ю работу и равна 0, если i-й рабочий не выполняет j-ю работу.

2. Определим функцию цели. Модель, которую нужно минимизировать имеет следующий вид:

Z =  C_ij* X_ij

Где Z - суммарная стоимость выполнения всех работ.

3. Опишем ограничения модели:

 X_ij = 1 при i {1,4} - каждая работа должна быть выполнена только один раз.

 X_ij = 1 при j {1,4} - каждый рабочий должен выполнить только одну работу.

Оформим задачу на листе EXCEL.

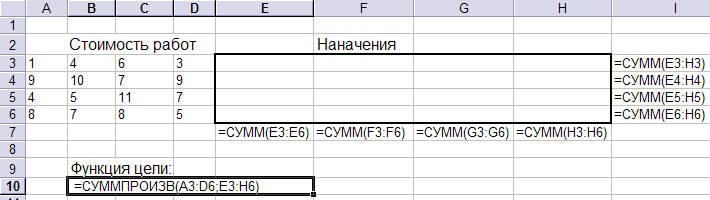
Внесите известные переменные C_ij в ячейки А1:D6.

Отведите под неизвестные переменные X_ij ячейки Е3:Н6

В ячейку В10 введите целевую функцию =СУММПРОИЗВ(А1:D6; Е3:Н6). Для написания формулы обратитесь к мастеру функций и не пишите вручную адреса ячеек – это основной источник ошибок в формулах.

Внизу и справа от ячеек с переменными X_ij запишите формулы, которые проверяют ограничения модели: суммы по строкам и столбцам переменных X_ij . В дальнейшем зададим их равными 1.

Вызовите Сервис/Поиск решения и заполните диалоговое окно c помощью мышки как показано ниже. Не забудьте в параметрах выставить линейную модель.

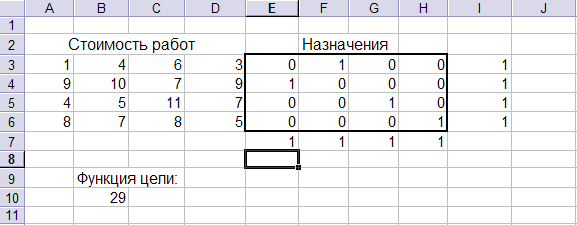
Поиск решения найдет решение:

7. Транспортная задача

Постановка задачи:

Фирма имеет 4 фабрики (Ф1,Ф2,Ф3,Ф4) и 5 центров распределения ее товаров (Ц1,Ц2,Ц3,Ц4,Ц5).

Фабрики имеют производственные мощности в 200, 150, 225 и 175 единиц продукции ежедневно, соответственно.

Центры распределения имеют ежедневную потребность в продукции в 100, 200, 50, 250 и 150 единиц продукции ежедневно.

Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в 0,75 ден. единицы в день, а штраф за просроченную поставку единицы продукции в центр распределения составляет 2,5 ден. единицы в день.

Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице:

Транспортные расходы, ден. единиц.

	Ц1	Ц2	Ц3	Ц4	Ц5
Ф1	1,5	2	1,75	2,25	2,25
Ф2	2,5	2	1,75	1	1,5
Ф3	2	1,5	1,5	1,75	1,75
Ф4	2	0,5	1,75	1,75	1,75

Цель: спланировать перевозки, сведя к минимуму суммарные транспортные расходы.

Случай 1. Условимся, что данная модель сбалансирована, т.е. суммарный объем произведенной продукции равен суммарному объему потребности центров.

Решение: