8. Основная формула фотограмметрии
Ф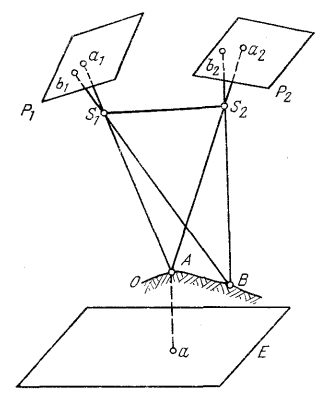
отограмметрия
- определяет формы, размеры и положение
объектов по их фотографическим
изображениям. Форму, размеры и положение
объекта можно определить, если
сфотографировать его с двух точек (рис.
1). Пусть
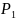и
—
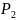пара снимков объекта О, полученная с
точек
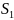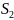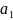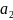и
;
,
и
,
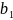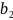-изображения
точек А и В объекта. Вообразим, что
объект после фотографирования удален.
По снимкам можно получить модель
объекта. Для этого достаточно придать
снимкам то положение, которое они
занимали относительно друг друга во
время съемки, и восстановить по ним
связки лучей, существовавшие в момент
фотографирования. Тогда каждая пара
соответственных лучей, например
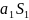и ,
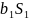или
и
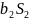будет пересекаться, в результате чего
образуется модель, подобная объекту.
Изменяя расстояние
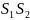между вершинами связок, можно получить
модель в любом масштабе. Модель используют
для измерения объекта. В частности,
после ориентирования модели относительно
планшета Е составляют карту. Точка а
на планшете получена в результате
ортогонального проектирования точки
А модели и указывает положение
соответствующей точки объекта на карте.
Метод измерения объектов, основанный
на использовании свойств пары снимков,
называется стереофотограмметрическим.
--------------------------------------------------------------------------------------
9. Средняя высота фотографирования
Фотосъёмка — фотографирование территории с большой высоты при помощи фотоаппарата, установленного на летательном аппарате:
1) на небольших высотах: на самолёте, вертолёте, беспилотном летательном аппарате;
2) на большой высоте: на спутнике или специальной ракете.
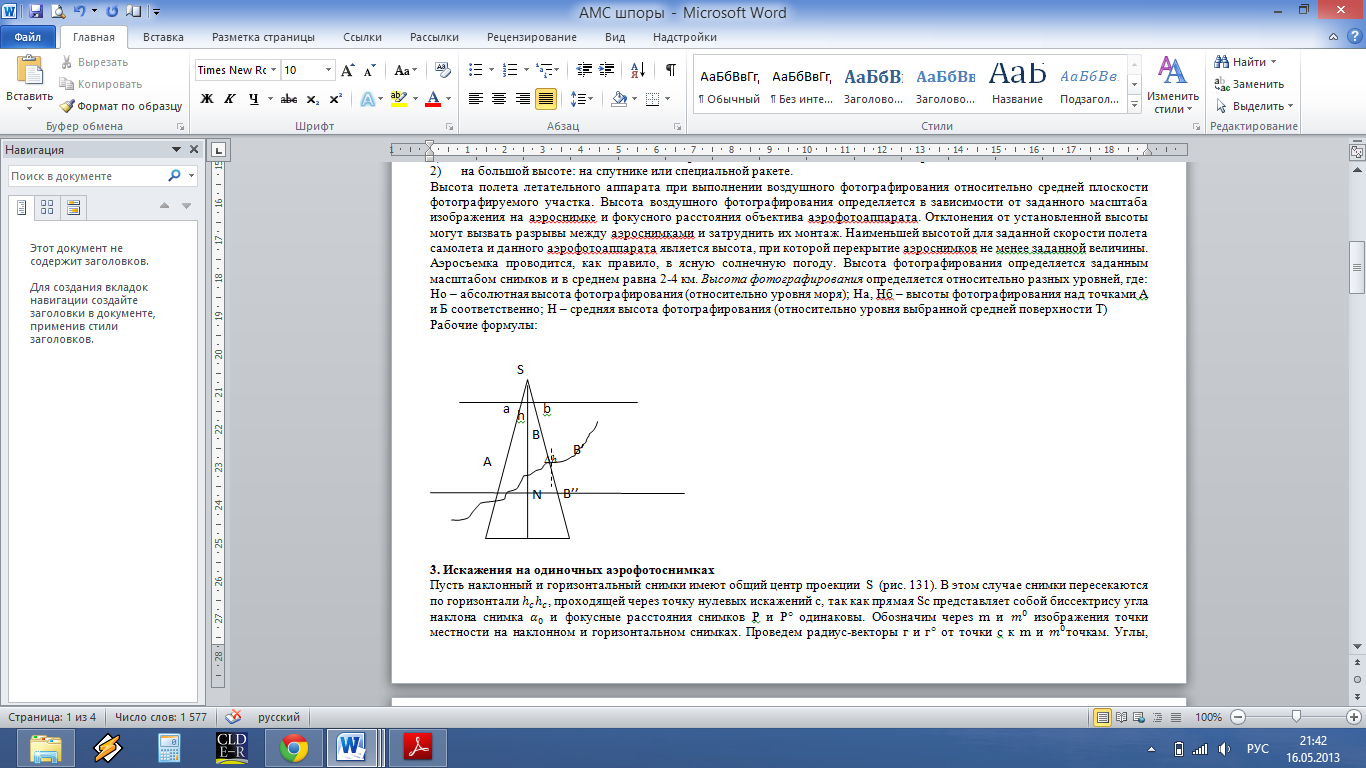
Высота полета летательного аппарата при выполнении воздушного фотографирования относительно средней плоскости фотографируемого участка. Высота воздушного фотографирования определяется в зависимости от заданного масштаба изображения на аэроснимке и фокусного расстояния объектива аэрофотоаппарата. Отклонения от установленной высоты могут вызвать разрывы между аэроснимками и затруднить их монтаж. Наименьшей высотой для заданной скорости полета самолета и данного аэрофотоаппарата является высота, при которой перекрытие аэроснимков не менее заданной величины. Аэросъемка проводится, как правило, в ясную солнечную погоду. Высота фотографирования определяется заданным масштабом снимков и в среднем равна 2-4 км. Высота фотографирования определяется относительно разных уровней, где: Но – абсолютная высота фотографирования (относительно уровня моря); На, Нб – высоты фотографирования над точками А и Б соответственно; Н – средняя высота фотографирования (относительно уровня выбранной средней поверхности Т)
-------------------------------------------------------------------------------------
10. Искажения на одиночных аэрофотоснимках
Пусть
наклонный и горизонтальный снимки
имеют общий центр проекции S
(рис. 131). В этом случае снимки пересекаются
по горизонтали
,
проходящей через точку нулевых искажений
с, так как прямая Sс
представляет собой биссектрису угла
наклона снимка
и фокусные расстояния снимков Р и Р°
одинаковы. Обозначим через m
и
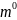изображения точки местности на наклонном
и горизонтальном снимках. Проведем
радиус-векторы г и г° от точки с к m
и
точкам.
Углы, составленные г и г° с линией
,
одинаковы. Поэтому если снимок Р
повернуть вокруг горизонтали
и совместить со снимком Р°, то радиус-вектор
г совпадет с г°, а точка m
наклонного снимка будет смещена
относительно точки m°
горизонтального снимка по радиусу-вектору
(рис. 132).
Таким образом, наклон снимка вызывает радиальные смещения точек. Точка m, лежащая выше линии неискаженного масштаба при наклоне снимка приближается к точке нулевых искажений с.
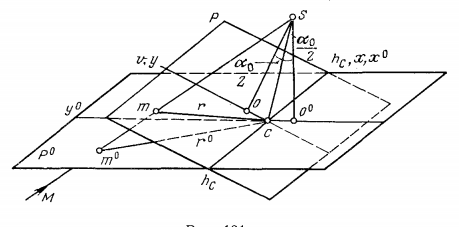
Рис.131
Если наклонный снимок совместить с горизонтальным, вращением его вокруг линии неискаженных масштабов (рис. 33.) то соответствующие точки окажутся на одном луче, проходящем через точку нулевых искажений c.
Разность
называется смещением точки за наклон
снимка. И понятно, что направлено оно
вдоль луча, проходящего через точку c.
Формула
величины смещения
(50)
Величина
смещения зависит и от фокусного
расстояния снимка. С его увеличением
она уменьшается. Для планового снимка
( 3°) величину максимального смещения
точек можно оценивать по приближенной
формуле:
.
Оно приводит к ошибкам в определении
по снимкам направлений, расстояний и
площадей.
Введя
дополнительно линию Ea на наклонном
снимке и, соответствующую ей линию, на
горизонтальном снимке. Как было
показано, точки на линии неискаженных
масштабов не смещаются, что относится
и к точке E, а точка
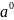изменила свое положение. В результате
изменилось направление E
на
угол δA. Этот угол и называют искажением
горизонтального направления на наклонном
снимке. Не трудно заметить
и с учетом приближенного соотношения
(50), а также того, что
получим
.(52)
Формула
(52) подтверждает, что направления не
искажаются, если они проходят через
точку нулевых искажений (т.е. при r=0), а
также показывает, что и направления
горизонталей не искажены (ɸ=90). Искажение
максимально приɸ=90. И если снимок
плановый, то его можно оценить по
приближенной формуле:
Рельеф
местности также вызывает смещение
точек, причем по направлениям проходящим
через точку надира n,в
которую сходятся изображения отвесных
прямых. То есть, если h - превышение
точки А над точкой В, расположенной
в плоскости предмета, и отрезок АВ
отвесный, то точка а на снимке сместится
относительно точки b на величину ab
= δ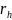
(рис. 35). При h > 0 смещение происходит
от точки надира, когда h < 0, – к точке
надира.
Данная формула дает хорошую оценку величины смещения точек за рельеф и для плановых снимков. Значит, по измеренной на плановом снимке величине смещения δ можно в ряде случаев с достаточной для практики точностью определить высоту отдельных объектов (дерева, столба, здания, трубы и т. д.).
Смещение точек за рельеф приводит на снимке и к искажению направлений отрезков, иногда довольно значительному.
------------------------------------------------------------------------------