14 10Ая система счисл

Десяти́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.

Один десятичный разряд в десятичной системе счисления иногда называют декадой. В цифровой электронике одному десятичному разряду десятичной системы счисления соответствует один десятичный триггер.

Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:

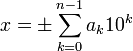, где   — это целые числа, называемые цифрами, удовлетворяющие неравенству 

Обычно для ненулевого числа x требуют, чтобы старшая цифра   в десятичном представлении x была также ненулевой.

Например, число сто три представляется в десятичной системе счисления в виде:

С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до  , то есть, всего   различных чисел.

Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:

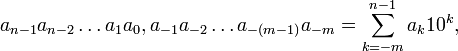
где n — число разрядов целой части числа, m — число разрядов дробной части числа.

15 Переход

Целая часть

Последовательно делить целую часть десятичного числа на основание, пока десятичное число не станет равно нулю.

Полученные при делении остатки являются цифрами нужного числа. Число в новой системе записывают, начиная с последнего остатка.

Дробная часть

Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.

Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.

Пример

 переведём в двоичную систему:

44 делим на 2. частное 22, остаток 0

22 делим на 2. частное 11, остаток 0

11 делим на 2. частное 5, остаток 1

5 делим на 2. частное 2, остаток 1

2 делим на 2. частное 1, остаток 0

1 делим на 2. частное 0, остаток 1

Частное равно нулю, деление закончено. Теперь записав все остатки снизу вверх получим число

 

16 Двоичная система счисления

Чт, 2009-12-31 13:43 — tech

Раздел: 

 Системы счисления

Номер темы: 

 2

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе: 0 – это ноль 1 – это один (и это предел разряда) 10 – это два 11 – это три (и это снова предел) 100 – это четыре 101 – пять 110 – шесть 111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 - это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

100010012 = 13710

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток) 38 / 2 = 19 (0 остаток) 19 / 2 = 9 (1 остаток) 9 / 2 = 4 (1 остаток) 4 / 2 = 2 (0 остаток) 2 / 2 = 1 (0 остаток) 1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

17 Высказывание — (термин из математической логики) это утверждение, которое является либо истинным, либо ложным. Логическое высказывание принято обозначать заглавной латинской буквой.

Высказывательной формой называется логическое высказывание, в котором один из объектов заменён переменной. При подстановке вместо переменной какого-либо значения высказывательная форма превращается в высказывание.

Пример: «В городе x идёт дождь.» — высказывательная форма, «В городе Архангельске идёт дождь.» — высказывание.

Содержание   [убрать]  1 Виды высказываний 2 Связь с математической логикой 3 Основные операции над логическими высказываниями 4 См. также 5 Примечания 6 Литература

Виды высказываний [править]

Логические высказывания принято подразделять на два вида: элементарные логические высказывания и составные логические высказывания.

Составное логическое высказывание — это высказывание, образованное из других высказываний с помощью логических связок.

Логическая связка — это любая логическая операция над высказыванием. Например, употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если… , то», «тогда и только тогда» являются логическими связками.

Элементарные логические высказывания — это высказывания не относящиеся к составным.

Примеры: «Петров — врач», «Петров — шахматист» — элементарные логические высказывания. «Петров — врач и шахматист» — составное логическое высказывание, состоящие из двух элементарных высказываний, связанных между собой при помощи связки «и».

Связь с математической логикой [править]

Обычная логика двухзначна, то есть приписывает высказываниям только два возможных значения: истинно оно или ложно.

Пусть   — высказывание. Если оно истинно, то пишут  , если ложно, то  .

Тождественно истинное высказывание обозначают символом 1, тождественно ложное — символом 0.

Существуют также многозначные логики (Яна Лукасевича, С. Клини и др.).

Основные операции над логическими высказываниями [править]

Отрицание логического высказывания — логическое высказывание, принимающее значение «истинно», если исходное высказывание ложно, и наоборот.

Конъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны.

Дизъюнкция двух логических высказываний — логическое высказывание, истинное только тогда, когда хотя бы одно из них истинно.

Импликация двух логических высказываний A и B — логическое высказывание, ложное только тогда, когда B ложно, а A истинно.

Равносильность (эквивалентность) двух логических высказываний — логическое высказывание, истинное только тогда, когда они одновременно истинны или ложны.

Кванторное логическое высказывание с квантором всеобщности ( ) — логическое высказывание, истинное только тогда, когда для каждого объекта x из заданной совокупности высказывание A(x) истинно.

Кванторное логическое высказывание с квантором существования ( ) — логическое высказывание, истинное только тогда, когда в заданной совокупности существует объект x, такой, что высказывание A(x) истинно.

18 Нетрудно привести примеры формул, которые «выражают одно и то же». Таковы, например, формулы XY и YX. Подобные формулы мы будем называть равносильными. Прежде, чем дать соответствующее определение, условимся о следующем обозначении.

Определение. Формулы F и G называются равносильными, если для любой интерпретации  выполняется равенство (F)=(G).

Убедимся в том, что формулы F=XY и G=XY равносильны. Ясно, что если интерпретации  и  совпадают на X и Y, то (F)=(F) и (G)=(G). Следовательно, для проверки равенства (F)=(G) из определения равносильности надо рассмотреть лишь интерпретации, которые различаются на X и Y (а таких интерпретаций четыре) и вычислить соответствующие значения (F) и (G). Другими словами, надо составить совместную таблицу истинности формул F и G (см. таблицу 1.2).

Таблица 1.2

X	Y	F=XY	X	G=XY
1	1	1	0	1
1	0	0	0	0
0	1	1	1	1
0	0	1	1	1

В таблице 1.2 для удобства вычисления значения интерпретаций на G введен промежуточный столбец X. Мы видим, что столбцы формул F и G совпадают. Это означает, что формулы F и G равносильны.

Близким к понятию равносильности является понятие тождественной истинности.

Определение. Формула F называется тождественно истинной если для любой интерпретации  выполняется равенство (F)=1.

Например, формула F=X&YX является тождественно истинной. Для проверки равенства (F)=1 не надо рассматривать все интерпретации, а лишь четыре, которые различаются на атомарных формулах X и Y. Для таких интерпретаций надо вычислить значение формулы F, т.е. составить таблицу истинности формулы F (см. таблицу 1.3). Таблица 1.3 для удобства вычисления значения (F) содержит промежуточный столбец X&Y.

Таблица 1.3

X	Y	X&Y	F=X&YX
1	1	1	1
1	0	0	1
0	1	0	1
0	0	0	1

Мы видим, что столбец формулы F состоит из одних единиц. Это означает, что формула F тождественно истинна.

Теорема 1.1. Формулы F и G равносильны тогда и только тогда, когда формула FG является тождественно истинной.

Доказательство. Предположим, что формулы F и G равносильны и рассмотрим интерпретацию . Ясно, что (FG)=(F)(G). Поскольку значения истинности (F) и (G) совпадают, то по таблице истинности эквиваленции имеем равенства (F)(G)=1. Это означает, что формула FG тождественно истинна.

Предположим теперь, что формула FG тождественно истинна и рассмотрим интерпретацию . Имеем, что 1=(FG)=(F)(G). Но из таблицы истинности эквиваленции следует, что если (F)(G)=1, то (F)=(G).

Теорема доказана.

В логике высказываний довольно часто приходится проводить преобразования формул, сохраняющие равносильность. Для таких преобразований используются так называемые законы логики высказываний. Приведем список этих законов.

Пусть F,G и Н – некоторые формулы логики высказываний. Тогда следующие формулы равносильны:

1) F&1 и F;	2) F1 и F;
3) F&0 и 0;	4) F0 и F;
5) F&F и F;	6) FF и F;
7) F&G и G&F;	8) FG и GF;
9) F&(G&H) и (F&G)&H;	10) F(GH) и (FG)H;
11) F&(GH) и (F&G)(F&H);	12) F(G&H) и (FG)&(FH);
13) F&(FG) и F;	14) F(F&G) и F;
15) F&F и 0;	16) FF и 1;
17) (F&G) и FG;	18) (FG) и F&G;
19) F и F;	20) FG и FG;
21) FG и (FG)&(GF).

Доказательство этих равносильностей (законов логики высказываний) легко получается с помощью таблиц истинности. Отметим, что в примере на определение равносильности мы фактически доказали закон 20.

Прокомментируем список законов. Законы 5 и 6 называются идемпотентностью, 7 и 8 – коммутативностью, 9 и 10 – ассоциативностью соответственно конъюнкции и дизъюнкции. Ассоциативность конъюнкции означает, что в конъюнкции трех формул скобки можно ставить как угодно, а, следовательно, вообще не ставить. Из этого утверждения следует, что в конъюнкции четырех, пяти и т.д. любого конечного числа формул скобки можно ставить как угодно и поэтому вообще не ставить. Аналогичное замечание можно сделать и для дизъюнкции.

Законы 11 и 12 называются дистрибутивностями. Более точно, закон 11 – дистрибутивность конъюнкции относительно дизъюнкции, а закон 12 – дистрибутивность дизъюнкции относительно конъюнкции. Для применения этих законов в преобразованиях формул удобно иметь в виду следующий аналог. Заменим в законе 11 формулы F,G и Н соответственно буквами a,b и с, знак & заменим умножением *, а знак  – сложением+. Мы получим известное числовое тождество

a*(b+c)-a*b+a*c (*)

Это тождество есть дистрибутивность умножения чисел относительно сложения. В школе применение этого равенства слева направо называется раскрытием скобок, а справа налево вынесением общего множителя. Отличие операций над высказываниями & и  от числовых операций * и+состоит в том, что для высказываний выполняются обе дистрибутивности, а для чисел только одна. Сложение не дистрибутивно относительно умножения.

Закон 15 называется законом противоречия, закон 16 – законом исключенного третьего, закон 19 – снятием двойного отрицания. Законы 13 и 14 называются законами поглощения, а законы 17 и 18 – законами де Моргана в честь известного французского математика и логика 19 века.

Имея законы логики высказываний, мы получаем еще один способ доказательства равносильности двух формул, наряду с построением совместной таблицы истинности. Этот способ состоит в переходе от одной формулы к другой с помощью законов. В его основе лежит следующее легко доказываемое утверждение: если в некоторой формуле F заменить подформулу G равносильной ей формулой G′, то получим формулу F′, равносильную исходной формуле F. Проиллюстрируем второй способ на следующем примере: доказать равносильность формул

F=[X&(ZY)][(XZ)&Y] и

G=(XY)&(YZ).

В силу закона 20, формулы ZY и XZ равносильны соответственно формулам ZY и XZ, поэтому формула F равносильна формуле

F1=[X&(ZY)][(XZ)&Y].

Дважды применив дистрибутивность (закон 11) и пользуясь ассоциативностью связок & и , получим, что формула F1 равносильна формуле

F2=(XXZ)&(ZYXZ)&(XY)&(ZYY).

В силу коммутативности дизъюнкции, законов 16 и 2, формулы XXZ и ZYXZ равносильны 1. Применив теперь законы 1 и 6 и коммутативность дизъюнкции, получим, что формула F2 равносильна G.

19 Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.[1] Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.

Формулы в КНФ:

Формулы не в КНФ:

Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:

Построение КНФ [править]

Алгоритм построения КНФ [править]

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения КНФ [править]

Приведем к КНФ формулу

Преобразуем формулу F к формуле не содержащей → :

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

По закону дистрибутивности получим КНФ:

k-конъюнктивная нормальная форма [править]

k-конъюнктивной нормальной формой называют конъюнктивную нормальную форму, в которой каждая дизъюнкция содержит ровно k литералов.

Например, следующая формула записана в 2-КНФ:

Переход от КНФ к СКНФ [править]

Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение :  (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:

Таким образом, из КНФ получена СКНФ.

Формальная грамматика, описывающая КНФ [править]

Следующая формальная грамматика описывает все формулы, приведенные к КНФ:

<КНФ> → <дизъюнкт>

<КНФ> → <КНФ> ∧ <дизъюнкт>

<дизъюнкт> → <литерал>;

<дизъюнкт> → (<дизъюнкт> ∨ <литерал>)

<литерал> → <терм>

<литерал> → ¬<терм>

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Формулы в ДНФ:

Формулы не в ДНФ: