4.1.Теорема Блоха

Из трансляционной симметрии кристалла следует, что при трансляции кристалла на вектор решётки кристалл совмещается сам с собой. Поэтому волновые функции электрона до трансляции и после трансляции на вектор решётки описывают физически эквивалентные состояния. Из квантовой механики известно, что физически эквивалентные состояния определены с точностью до фазового множителя . Действительно, для эквивалентных состояний плотности вероятности должны быть одинаковы

, (1)

откуда следует, что

. (2)

Поскольку левая часть этого равенства зависит от и , то фаза должна быть функцией вектора решётки, т.е. . Для исследования этой зависимости представим произвольный вектор решётки в виде суммы векторов и , тогда

.

С другой стороны,

.

Откуда получаем условие линейной связи между и

.

Так как – величина скалярная и безразмерная, то линейную связь между и вектором решётки можно представить в виде скалярного произведения вектора на некоторый вектор с размерностью, обратной размерности вектора решётки, т.е. м^-1:

. (3)

Подставляя в (2), окончательно имеем

. (4)

Теорема Блоха (1-ая формулировка): для любой волновой функции , удовлетворяющей уравнению Шрёдингера, существует такой вектор , что трансляция на вектор решётки эквивалентна умножению этой функции на фазовый множитель .

Часто используют другую, эквивалентную формулировку.

Теорема Блоха (2-ая формулировка): состояние электрона в кристалле описывается плоской волной, амплитуда которой есть периодическая функция с периодом, равным вектору решётки:

, (5)

где амплитуда .

Докажем эквивалентность 2-ой и 1-ой формулировок теоремы Блоха. Запишем формулу (2) для состояния электрона в точке :

_.

Откуда следует 1-ая формулировка теоремы Блоха: .

Поскольку правая часть формулы (5) зависит от вектора , то волновую функцию также необходимо обозначить индексом « ».

4.2. Понятие квазиимпульса

Итак, соответствие с теоремой Блоха, состояние электрона в кристалле описывает «блоховская» волна:

. ( )

Как видно, блоховская волна отличается от состояния свободно движущейся частицы

, (6)

тем, что в последнем случае амплитуда волны не зависит от координат, т.е. А=const.

«Обычная» плоская волна де Бройля (6), как известно, является собственной функцией оператора импульса и оператора Гамильтона для однородного пространства, т.е.

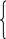
, при

Поэтому в состоянии сохраняется импульс частицы и полная энергия , которая совпадает с её кинетической энергией.

Силовое поле кристалла является периодической функцией координат, т.е. , поэтому импульс электрона в кристалле не сохраняется. Но из теоремы Блоха (5) следует, что сохраняется некоторый вектор с размерностью импульса . Этот вектор называется квазиимпульсом, а квазиволновым вектором.

По определению квазиимпульс есть вектор , сохранение которого следует из трансляционной симметрии кристалла, т.е. из инвариантности гамильтониана относительно трансляции на вектор решётки.

Это отличает его от обычного импульса , сохранение которого следует из полной трансляционной симметрии однородного пространства, т.е. из инвариантности гамильтониана относительно трансляции на любой вектор.

Очевидно, что при выглаживании потенциального рельефа кристалла, например, при стремлении к нулю параметра решётки , , пространство станет однородным и квазиимпульс станет равным импульсу, который теперь будет хорошим интегралом движения электрона.

Поэтому оператор квазиимпульса удобно представить в виде суммы оператора импульса и некоторого оператора , который должен стремиться к нулю при выглаживании потенциального рельефа кристалла, т.е.

. (7)

Так как в кристалле сохраняется квазиимпульс электрона , то блоховские волны будут собственными функциями оператора квазиимпульса

. (8)

Подставляя в (8) формулы (7) и ( ), получим

,

откуда:

. (9)

Окончательно оператор квазиимпульса запишем в виде:

. (10)

При выглаживании потенциального рельефа амплитуда блоховской волны будет стремиться к константе, т.е. и , поэтому оператор квазиимпульса будет иметь вид , что совпадает с оператором импульса и соответственно квазиимпульс перейдёт в импульс .

Отличительной чертой квазиимпульса является его неоднозначность. Для рассмотрения этого свойства квазиимпульса необходимо использовать понятие обратной решётки.