3.5. Законы Дебая и Дюлонга-Пти

При низких и высоких температурах интерполяционная функция Дебая выражается через простые функции.

Рассмотрим область низких температур, . В этой области х_пр>>1 и верхний предел в интеграле формулы (18) можно положить равным бесконечности, тогда для интеграла получим табличное значение

(19)

Для тепловой энергии одного моль вещества соответственно получим

, (20)

а для молярной теплоёмкости

(21)

Формула (21) выражает закон Дебая в области криогенных температур.

Рассмотрим теперь область высоких температур, , х_пр<<1, а следовательно и переменная х<<1, что позволяет разложить функцию е^х в ряд Маклорена по малому параметру х: . Интеграл в правой части выражения (18) будет равен , а само выражение для тепловой энергии будет линейной функцией температуры Е(Т)=9N_атk_BT. Для теплоёмкости одного моля вещества в твёрдом состоянии получается закон Дюлонга-Пти:

(22)

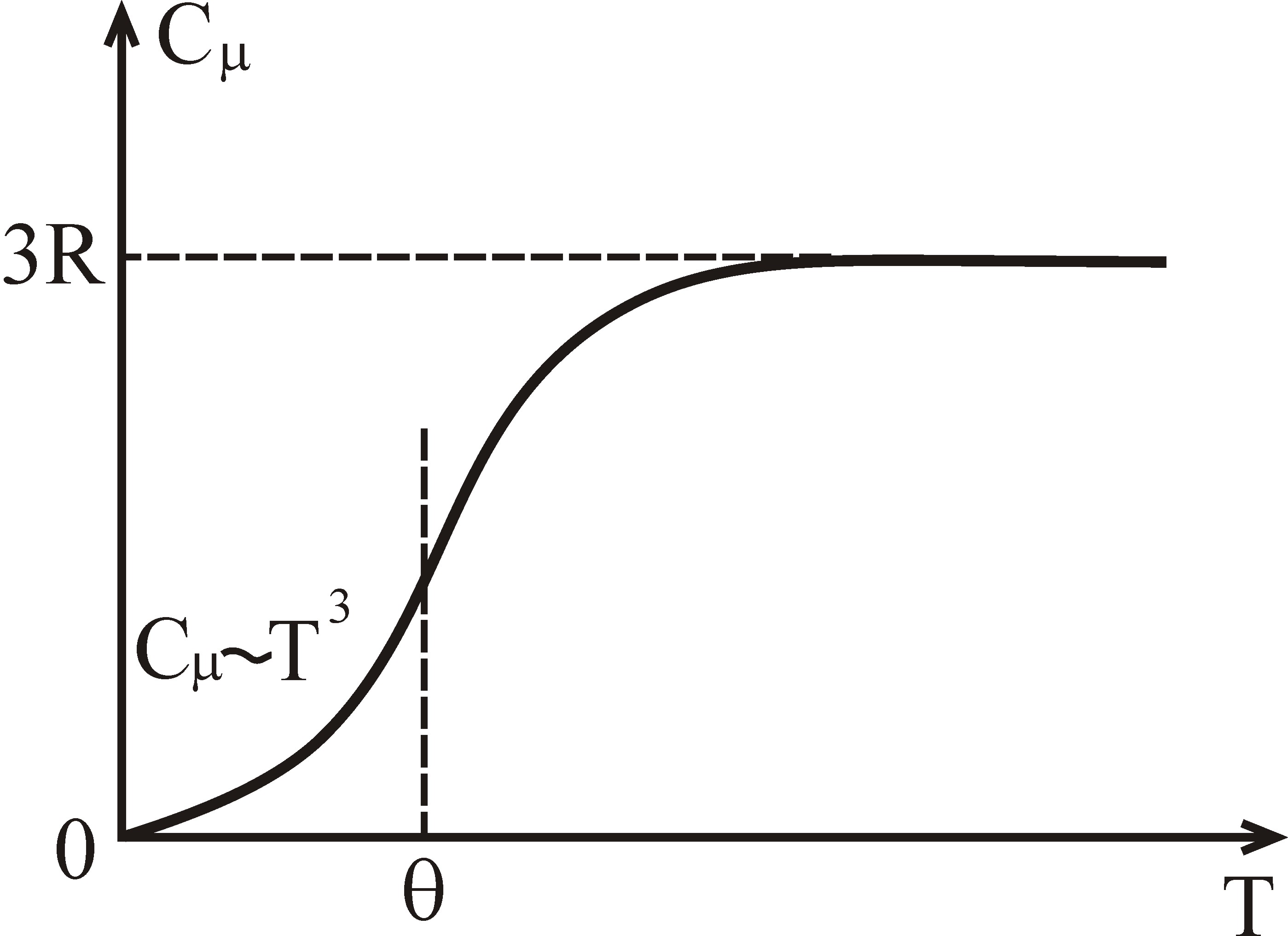
Рис. 3.3. Температурная зависимость теплоёмкости кристалла по теории теплоёмкости Дебая

На рис. 3.3 представлена зависимость от температуры молярной теплоёмкости кристалла в соответствии с квантовой теорией теплоёмкости Дебая, которая хорошо объясняет экспериментальную зависимость теплоёмкости диэлектриков за исключением области предплавильных температур, где наблюдается отклонение от закона Дюлонга-Пти из-за сильного ангармонизма колебаний атомов решётки.

Экспериментальные данные по температурной зависимости теплоёмкости металлов хорошо аппроксимируются следующей формулой:

. (23)

Первый член, линейный по температуре, обусловлен вкладом в теплоёмкость электронов проводимости, а второй – кубический, обусловлен колебаниями атомов решётки.

3.6. Физический смысл температуры Дебая

Температура Дебая разделяет температурную область, при которой существует кристалл (от 0 К до температуры плавления ) на две области: при нагревание кристалла носит дискретный, квантовый характер; в кристалле последовательно с ростом температуры заполняются фононами частотные уровни от 0 до предельной частоты . При температурах в основном возбуждаются дебаевские фононы, т.е. фононы с предельной частотой , что соответствует представлениям классической теории теплоёмкости кристалла. Таким образом, при высоких температурах нагревание кристалла носит квазиклассический характер. Для количественной оценки температуры Дебая в формулу для дебаевской температуры подставим выражение (16) для предельной частоты и получим:

. (24)

Для одноатомного кристалла с простой кубической решёткой атомный объём равен объёму элементарной ячейки, т.е. а³. В этом случае имеем:

.

Полагая, для примера а 0.3 нм, 3 км/с, получим К.

Глава 4. ЭлЕктронные состояния в кристалле

Уравнение Шрёдингера для кристалла представляет многочастичную задачу. Проблема многих тел – одна из трудных проблем теоретической физики. С помощью адиабатического приближения и приближения самосогласованного поля уравнение Шрёдингера для кристалла сводится к одночастичному уравнению Шрёдингера. Оно состоит в нахождении собственных функций и значений энергии электрона в самосогласованном поле. Явный вид потенциала этого поля построить невозможно из-за большого количества частиц, участвующих в его формировании, включая рассматриваемый электрон.

Самосогласованное (эффективное) поле, однако обладает трансляционной симметрией кристалла, что позволяет исследовать основные свойства электронных состояний и дисперсионных соотношений для электрона в кристалле. С симметрией потенциального рельефа всегда связаны некоторые законы сохранения. Из трансляционной симметрии кристалла следует сохранение величины с размерностью импульса, называемой квазиимпульсом. Квазиимпульс является интегралом движения электрона в идеальном кристалле и выполняет роль квантового числа, классифицирующего собственные функции и собственные значения энергии электрона.