3.2. Плотность состояний фононного спектра

Выражение для тепловой энергии кристалла (1) представляет сумму большого числа (порядка или более числа Авогадро), слагаемых, поэтому это выражение удобно записать в интегральной форме. Для того, чтобы перейти от суммы к интегралу вводится функция плотности состояния фононного спектра.

Пусть N есть число состояний с частотами от 0 до . Тогда производная , называемая плотностью состояния фононного спектра, есть число состояний, приходящихся на единичный интервал частот, а dN – число состояний с частотами от до . Энергия фононов dE на этом бесконечно малом участке спектра очевидно равна

, (5)

где энергия фононного уровня, вероятность заполнения этого уровня, которая определяется распределением Планка (4), а число квантовых состояний, приходящихся на интервал . Интегрируя (5) по всем нормальным частотам, получим тепловую энергию кристалла

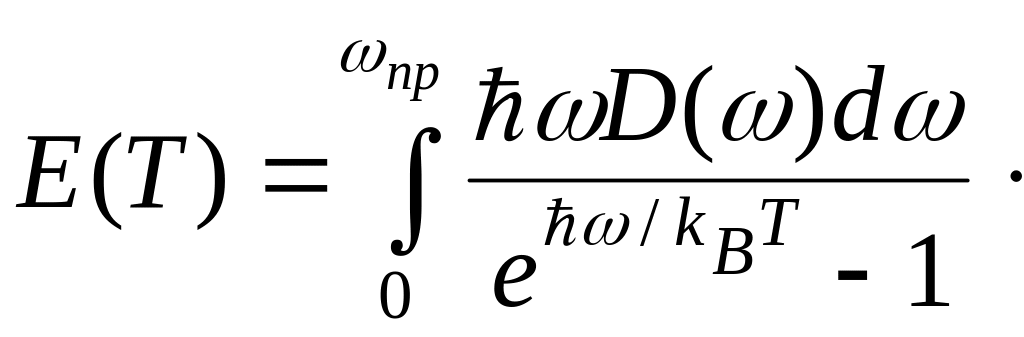(6)

Для расчёта функции используют граничные условия Борна-Кармана и предположения относительно линейности и изотропности закона дисперсии фононов.

3.3. Циклические граничные условия Борна-Кармана

Для того, чтобы исключить поверхностные эффекты для кристалла конечных размеров, используют циклические граничные условия, путем сшивания упругой волны смещения (волновой функции фонона) на границе кристалла:

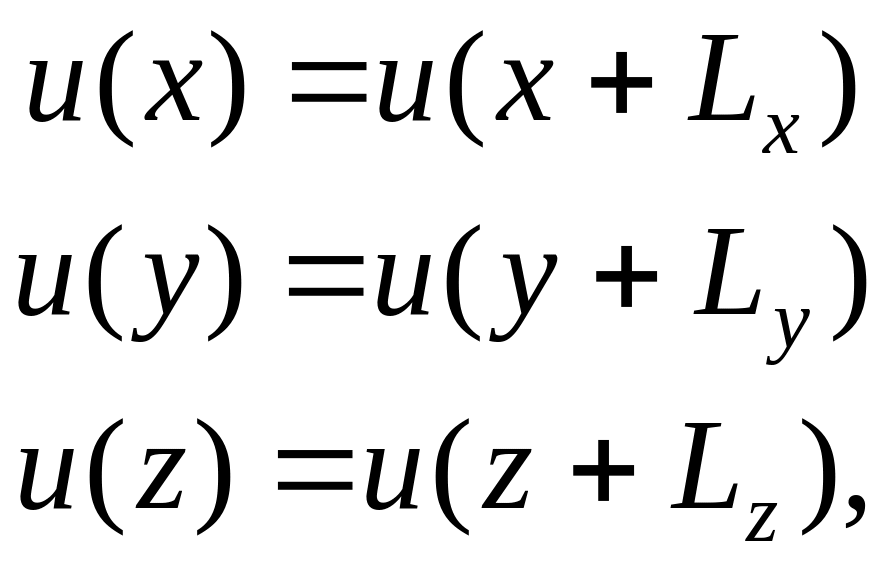(7)

где L_x, L_y, L_z – размеры кристалла в направлениях x, y, z.

В одномерном случае упругая волна смещения имеет вид

. (8)

Подставляя её в граничное условие (8), получим

. (9)

С учетом формулы Эйлера , получим решение (9) в виде

, где п= .

Таким образом, на одно квантовое состояние на оси k_x приходится отрезок , не зависящий от квантового числа п. Повторяя эти вычисления для упругих волн в направлениях y и z получим соответственно: . Поэтому в трёхмерном случае на одно квантовое состояние в k-пространстве приходится объём , определяемый следующей формулой

, (10)

где V=L_xL_yL_z – объём кристалла.

3.4. Интерполяционная формула Дебая

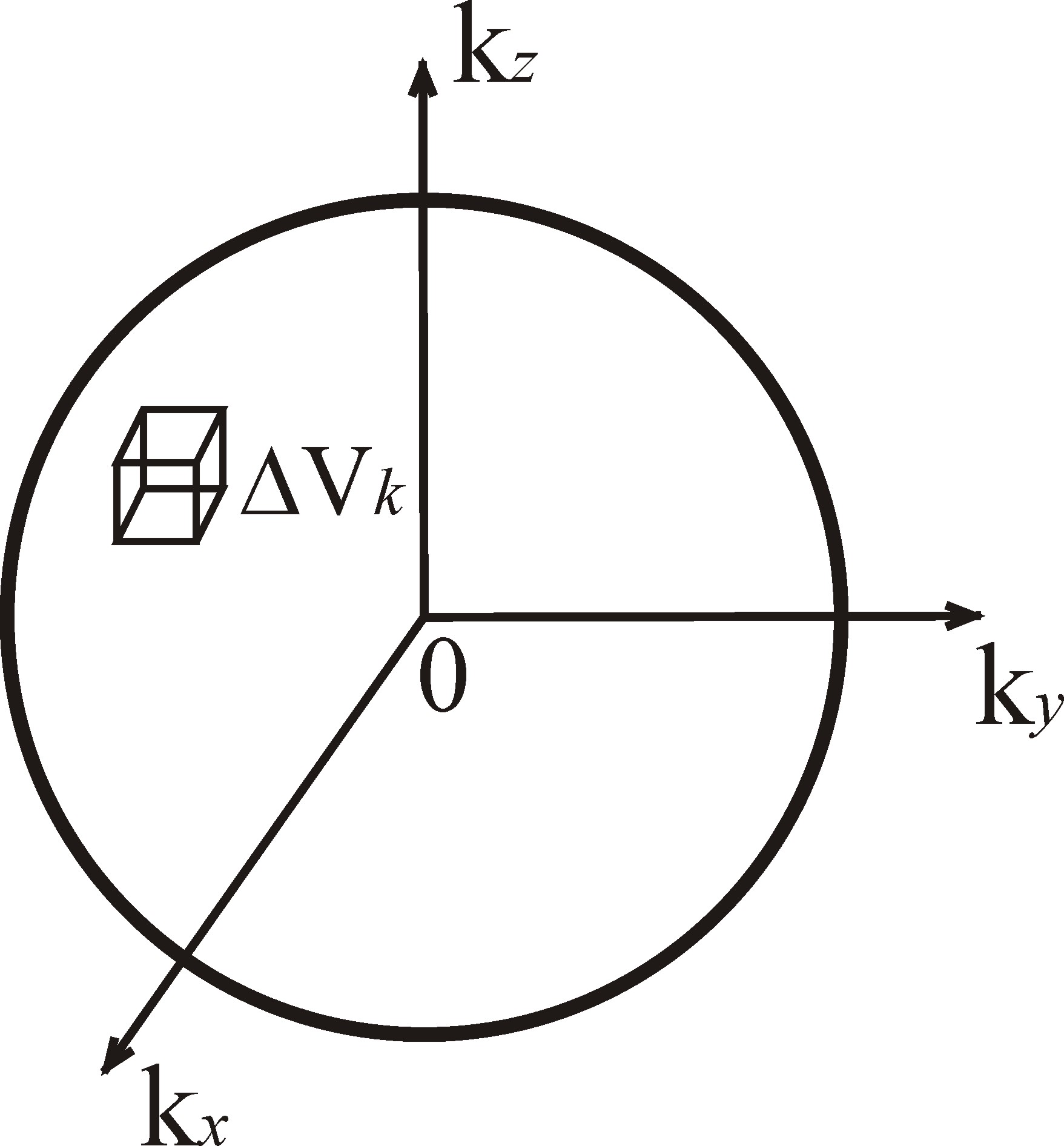
Для вычисления явного вида функции плотности состояния вычислим сначала количество квантовых состояний N c частотами от 0 до . Из линейного закона дисперсии фононов следует, что поверхность постоянной частоты в k-пространстве есть сфера (Рис. 3.2). Внутри этой сферы находятся все состояния с частотами от 0 до .

Рис. 3.2. Поверхность постоянной частоты в k-пространстве для трёхмерного кристалла с изотропным законом дисперсии фононов

Количество таких состояний можно подсчитать, поделив объём k-пространства, в котором находятся все состояния с частотами от 0 до , т.е. объём шара радиусом , на объём , приходящийся на одно квантовое состояние. В результате получим

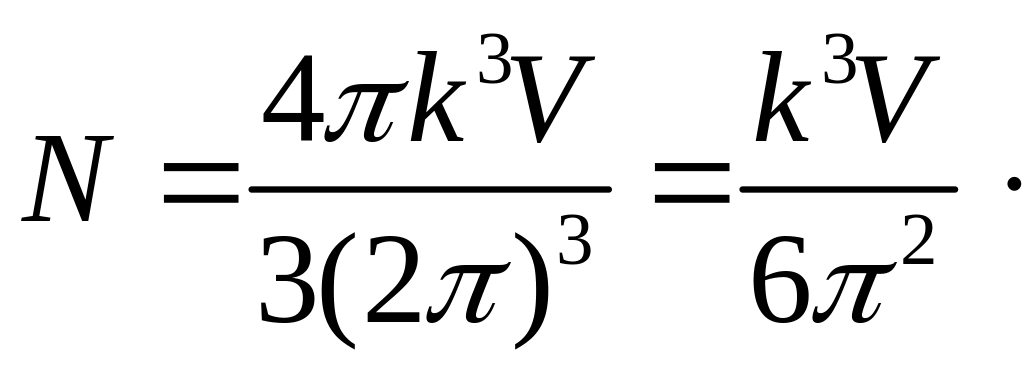(11)

Зависимость можно получить из (11) с использованием закона дисперсии фононов :

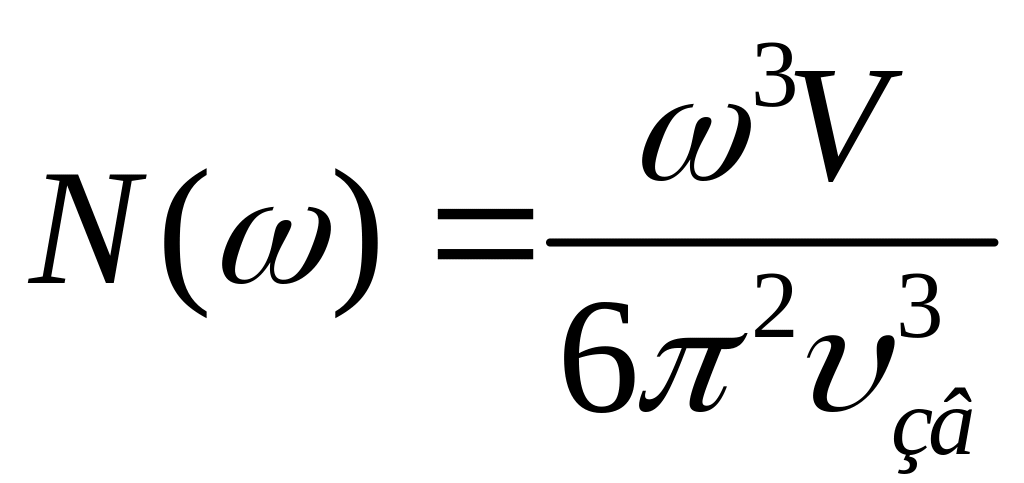, (12)

откуда для функции плотности состояний фононного спектра , имеем:

(13)

До сих пор мы учитывали только один тип колебаний кристалла. В трёхмерном одноатомном кристалле необходимо учитывать три моды акустических колебаний: продольную моду колебания и две поперечные моды. (Для кристалла с базисом, когда элементарная ячейка содержит два и более атома, надо ещё учитывать три моды оптических колебаний). С учётом этих рассуждений функция плотности состояний фононного спектра трёхмерного одноатомного кристалла будет иметь вид

, (14)

где множитель 3 учитывает три моды акустических колебаний. Функция плотности состояний должна удовлетворять условию нормировки

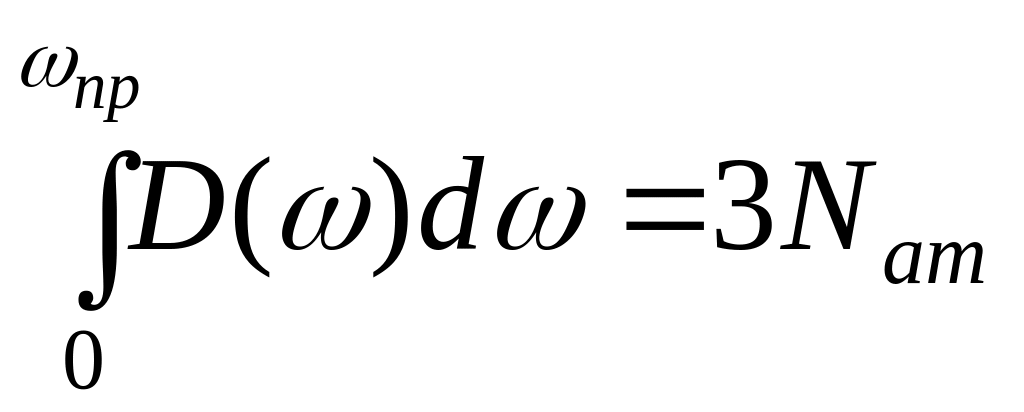, (15)

где 3N_ат есть число степеней свободы трёхмерного кристалла за вычетом 6-ти степеней свободы кристалла как целого: трёх степени свободы, связанных с поступательным движением кристалла, и трёх – с вращательным. Подставляя (14) в (15), получим выражение для предельной частоты фононного спектра

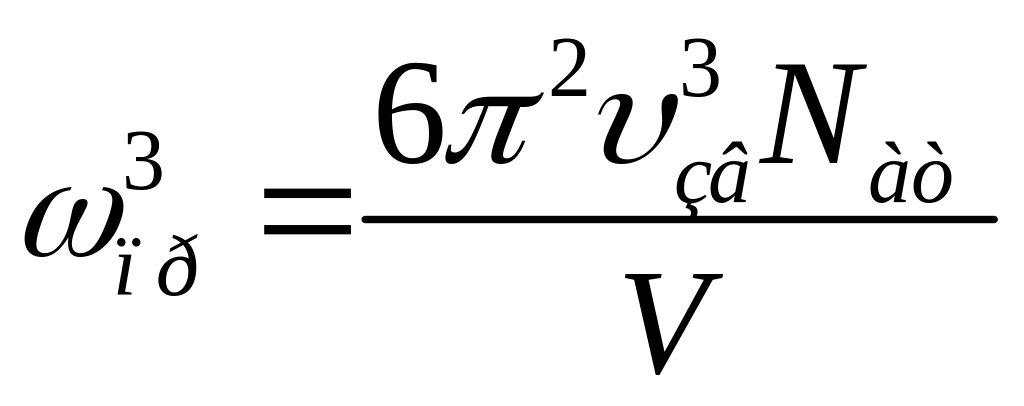. (16)

Подставим теперь полученную функцию плотности состояния (14) в выражение для тепловой энергии кристалла (6):

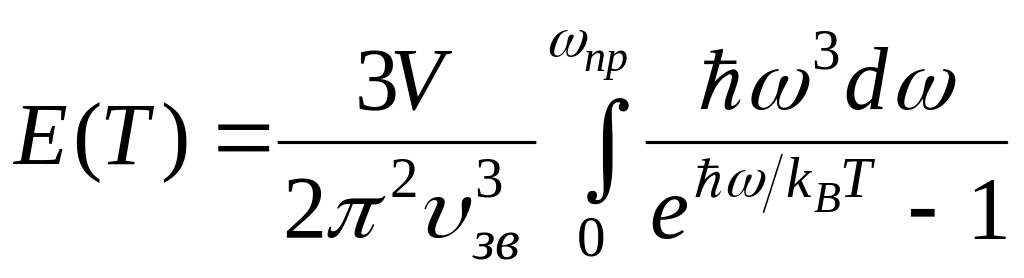. (17)

Обозначим через х переменную , тогда . Из условия , можно заключить, что существует характеристическая температура , называемая температурой Дебая, при которой возбуждается предельная частота в спектре . Следовательно, предельное значение величины х можно выразить как отношение дебаевской температуры к текущей температуре, т.е. . Перепишем формулу для тепловой энергии, учитывая выражение для предельной частоты (16), в результате получим

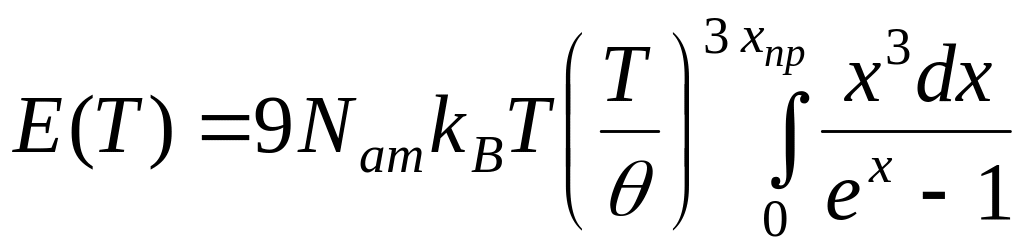. (18)

Это выражение называется интерполяционной формулой Дебая. Она позволяет численным методом построить зависимость Е(Т) при любых температурах.