Глава 3. Квантовая теория тЕплоёмкосТи кристалла

Классическая теория теплоёмкости кристаллической решётки основана на предположениях, что при любой температуре атомы кристалла совершают колебания относительно своих положений равновесия с одинаковой частотой, а на одну степень свободы колебательного движения атома в среднем приходится энергия . При этих предположениях теплоемкость кристалла оказалась независящей от температуры и для одного моля вещества имеет значение , (где R – универсальная газовая постоянная) – закон Дюлонга-Пти (1819 г.).

Закон Дюлонга-Пти подтверждается экспериментально для различных веществ в широкой области температур, от комнатной до предплавильных. Однако эксперименты в области низких температур показали, что при уменьшении температуры до значения, близкого к абсолютному нулю, теплоёмкость различных кристаллов стремится к нулю по закону . Это так называемый закон Дебая. Низкотемпературные измерения теплоёмкости твёрдых материалов были выполнены впервые в Лейдене (Голландия) после создания Камерлинг-Оннесом в 1907 г. лаборатории низких температур на базе станции получения жидкого гелия.

Первая квантовая теория теплоёмкости кристалла была предложена А.Эйнштейном в 1907 г. Теория теплоёмкости Эйнштейна основана на предположении о том, что в частотном спектре кристалла существует единственная частота , вероятность заполнения которой определяется квантовым распределением Планка. Теория Эйнштейна предсказывала стремление к нулю теплоёмкости при , однако она давала температурную зависимость теплоёмкости, не согласующуюся с экспериментальными данными в области низких температур.

Более успешная квантовая теория теплоёмкости была развита Дебаем в 1912 г. Теория Дебая учитывала возбуждение всего спектра нормальных частот кристалла при нагревании и хорошо описывала температурную зависимость теплоёмкости кристаллов от температур, близких к абсолютному нулю до предплавильных температур.

3.1. Модель Дебая

В гармоническом приближении тепловая энергия кристалла представляет сумму энергии фононов с нормальными частотами от 0 до .

. (1)

В строго гармоническом приближении фононы с различными частотами не взаимодействуют между собой, а совокупность невзаимодействующих фононов не образует идеальный газ, поскольку для установления теплового равновесия в газе необходимо некоторое взаимодействие, потенциальная энергия которого должна быть много меньше средней кинетической энергии частиц газа. Взаимодействие между фононами возникает при учёте ангармонических членов разложения потенциала парного взаимодействия атомов решётки.

В гармоническом приближении число фононов n с данной энергией сохраняется, так как оператор числа фононов коммутирует с оператором Гамильтона осциллятора, т.е. . В слабо ангармоническом приближении оператор ангармоничности играет роль возмущения, которое нарушает условие коммутативности операторов и , т.е. . Поэтому в ангармоническом приближении число фононов в данном состоянии не является интегралом движения. Несохранение числа фононов с частотой при сохранении полной энергии кристалла означает, что фононы обмениваются состояниями с различными частотами и можно говорить лишь об их среднем значении в данном состоянии, . Поэтому в слабо ангармоническом приближении тепловая энергия кристалла имеет вид

. (2)

Несохранение числа фононов с частотой означает взаимодействие фононов, в результате которого часть фононов выбывает из состояния с одной частотой, а число фононов с другой (другими) частотой (частотами) увеличивается. При этом возможны реакции распада фонона на два и более фононов или, напротив, рождение одного фонона в результате взаимодействия двух и более фононов.

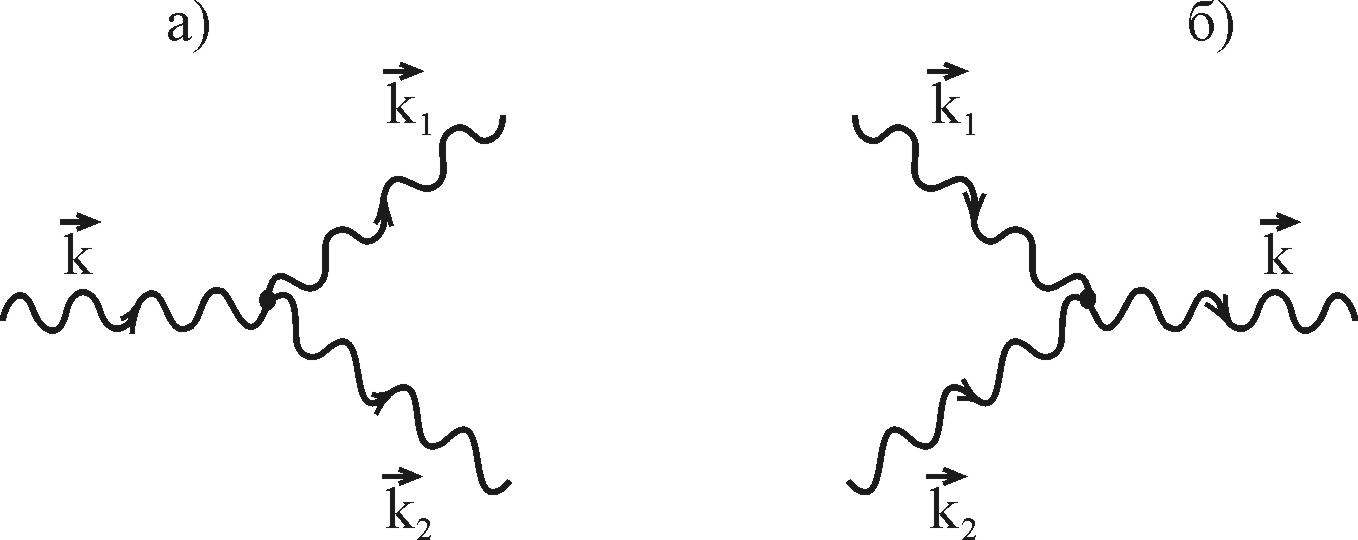
Рис. 3.1. Типичные двухфононные процессы: распад фонона (а) и рождение фонона в результате взаимодействия двух фононов

В результате фонон-фононного взаимодействия фононы помимо частоты, волнового вектора и поляризации будет характеризоваться ещё временем жизни и длиной свободного пробега.

Взаимодействие фононов обеспечивает установление теплового равновесия фононного газа. В соответствии с квантово-корпускулярным дуализмом фононам как квазичастицам соответствуют упругие волны смещения атомов кристалла. С ростом температуры в кристалле возбуждаются упругие волны с более высокими частотами. Этому процессу соответствует рождение фононов с более высокими частотами вплоть до предельной частоты . Упругие волны и соответствующие им фононы возбуждаются (и исчезают) по одиночке. Поэтому фононы являются бозонами. Как известно бозоны (частицы с целым спином) рождаются (исчезают) по одиночке, а фермионы (частицы с полуцелым спином) – парами. Это непосредственно связано с законом сохранения углового момента в квантовой механике и правилами его квантования. Таким образом, фононы образуют бозе-газ и подчиняются статистике Бозе-Эйнштейна. Запишем функцию распределения Бозе-Эйнштейна

, (3)

где среднее число частиц с энергией , химический потенциал бозе-газа. По определению , где F – свободная энергия газа, а N – число частиц.

При нагревании кристалла возбуждаются фононы с различными частотами, поэтому фононный газ представляет собой систему с переменным числом частиц. Общим условием термодинамического равновесия газа с переменным числом частиц является минимальное значение свободной энергии системы, т.е. . Но это означает, что в условиях равновесия химический потенциал фононного газа равен нулю. В этом случае, как и в случае фотонного газа, распределение Бозе-Эйнштейна (3) переходит в распределение Планка

(4)

Таким образом, в квантовой теории теплоёмкости Дебая кристалл при температуре Т моделируется как ящик с идеальным газом фононов, статистика которых определяется функцией распределения Планка (4). В теории Дебая предполагается, что закон дисперсии фононов линейный и изотропный, т.е. .