2.3. Колебания одномерного кристалла с двумя атомами в элементарной ячейке

На рис. 2.6 показано схематическое изображение участка одномерного двухатомного кристалла, в элементарной ячейке которого имеются различные атомы массой т и М.

Рис. 2.6. Одномерный двухатомный кристалл

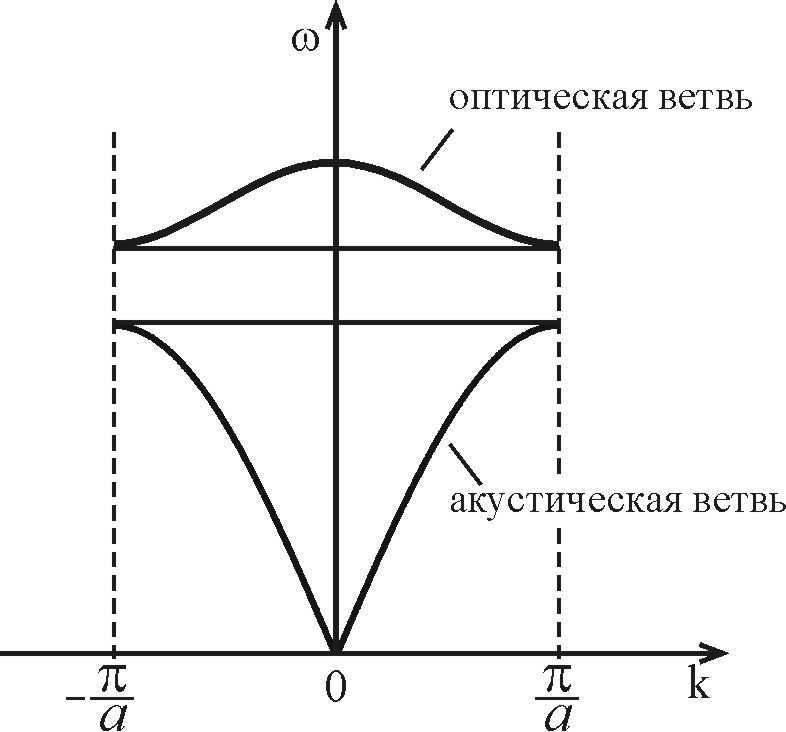
В таком кристалле возможны два типа колебаний: акустические и оптические. В акустических колебаниях осциллируют центры масс элементарных ячеек. При оптических колебаниях центры масс ячеек остаются неподвижными, а атомы, образующие элементарную ячейку, осцилируют друг относительно друга. Оптическая ветвь закона дисперсии отделена запрещённой зоной от акустической ветви и имеет максимальную частоту , где приведённая масса элементарной ячейки.

Рис. 2.7. Законы дисперсии оптических (верхняя кривая) и акустических (нижняя кривая) колебаний кристалла

В одномерном кристалле существуют только продольные волны, а в трёхмерном кристалле, кроме того, – две поперечных. Таким образом, в трёхмерном кристалле существуют шесть мод колебаний: три в акустической ветви и три в оптической ветви.

Оценим количественно характерные частоты в спектре акустических и оптических колебаний. Предельную частоту в спектре акустических колебаний выразим через скорость звука : . Скорость продольных и поперечных упругих волн составляет обычно 3-5 км/с, а межатомное расстояние м. Полагая, для примера, , а=3 10^-10 м, получим оценку предельной циклической частоты акустических колебаний , что соответствует максимальной частоте колебаний Гц и периоду колебаний c. Оптические колебания характерны, например, для ионных кристаллов типа NaCl и возбуждаются световой волной в инфракрасном диапазоне. В переменном электрическом поле световой волны катионы и анионы элементарной ячейки движутся в противоположные стороны, что приводит к поглощению энергии световой волны и возбуждению оптических колебаний ионного кристалла. Массы атомов элементарной ячейки обычно отличаются не более чем в два раза, поэтому предельная частота оптических колебаний превосходит предельную частоту акустических колебаний не более, чем на десятки процентов, т.е. является величиной того же порядка .

Минимальную частоту акустической ветви обычно полагают равной нулю, что соответствует бесконечной длине волны с учётом линейного закона дисперсии в длинноволновой области спектра . Для кристалла размером L_x минимальная циклическая частота есть , а обычная частота колебаний . Для кристалла размером L_x=1 см получим Гц, т.е. на семь порядков меньше предельной частоты Гц. Обычно минимальную частоту считают равной нулю, так как реально , что, строго говоря, соответствует приближению бесконечного кристалла.

2.4. Колебания атомов в трехмерном кристалле

Рассмотрим колебания атомов в трёхмерном кристалле с одним атомом в элементарной ячейке. Сила, действующая на атом в трёхмерном кристалле, получается в результате сложения упругих сил со стороны других атомов кристалла. Обозначим вектор смещения n-ого атома из положения равновесия в момент времени t как , где радиус вектор n-ого атома в момент времени t, а  вектор решётки, определяющий положение равновесия n-ого атома в одноатомном трёхмерном кристалле. Уравнение движения n-ого атома запишем в виде

, (1)

где т – масса атома, а с_nl – жесткость упругой связи («пружины») между атомами под номерами n и l. Так как массы всех атомов одинаковы, поделим уравнение (1) на т и введём динамическую матрицу . Элементы динамической матрицы имеют размерность квадрата частоты с^-2. Перепишем (1) в виде:

(2)

Здесь индексы n и l независимо друг от друга пробегают один и тот же ряд значений n,l=1,2…N_ат. Поэтому (1) или (2) есть система зацепляющихся дифференциальных уравнений. Одним из эффективных методов решения таких систем является метод нормальных координат.

Суть его состоит в следующем: вместо переменных вводятся новые обобщённые координаты . Переход от одних координат к другим в общем случае осуществляется с помощью унитарного преобразования

, (3)

(4)

где b_nm и – матрицы прямого и обратного унитарного преобразования соответственно, а n и m независимо друг от друга пробегают значения: 1,2…N_ат. Преобразования (3) и (4) можно записать в более компактной, операторной форме:

, ( )

, ( )

где и – векторы в пространстве, размерность которого равна числу степеней свободы трёхмерного кристалла N=3N_ат. (Строго говоря, число степеней свободы кристалла есть N=3N_ат – 6, где учитываются три вращательные степени свободы и три, связанные с поступательным движением всего кристалла. Так как число атомов в 1 см³ порядка , то обычно принимают N=3N_ат.). и операторы прямого и обратного унитарного преобразования.

Унитарные преобразования, как известно, не изменяют скалярного произведения векторов, в частности, модуля вектора и соответственно его размерности. Основное свойство унитарного преобразования состоит в следующем

, (5)

где – единичный оператор.

Систему зацепляющихся дифференциальных уравнений (2) удобно также записать в операторной форме

, (6)

где – «динамический» оператор; в результате его действия на вектор получается вектор ускорения, взятый со знаком минус, т.е. .

Подставим ( ) в (6) и подействуем слева на полученное уравнение оператором обратного унитарного преобразования :

. (7)

Здесь мы учли, что унитарный оператор действует только на пространственные координаты, поэтому . Используя условие унитарности (5) и обозначая оператор , получим

. (8)

До сих пор все преобразования (2) – (8) носили тождественный характер. Выберем теперь унитарный оператор таким, чтобы вектор был собственным вектором оператора , т.е.

. (9)

Так как унитарное преобразование не изменяет размерности, то размерность собственных значений оператора должна совпадать с размерностью элементов динамической матрицы, т.е. иметь размерность квадрата частоты. Поэтому из соображения размерности обозначим и запишем уравнение (8) в виде

. (10)

Спроектируем это уравнение на j-ую степень свободы:

, (11)

где q_j – компонента вектора в N-мерном пространстве, т.е. , а j пробегает значения: 1,2,3…N, где, как и ранее, N=3N_ат – число степеней свободы кристалла. Учитывая, что в преобразованиях (3) и (4) введены векторы , перепишем (11) в векторной форме

, (12)

где т пробегает значения: 1,2…N_ат.

Совокупность уравнений (11) представляет собой уравнения одномерных гармонических осцилляторов, которые независимо друг от друга колеблются с частотами .Частоты называются нормальными частотами кристалла, а коллективные координаты q_j – нормальными координатами или нормальными колебаниями кристалла.

Таким образом, нормальные координаты, определяемые условием (9), позволяют преобразовать систему зацепляющихся дифференциальных уравнений (1), описывающих колебания отдельных атомов, к совокупности уравнений нормальных колебаний кристалла. Из определения (4) и уравнения (12) следует, что нормальное колебание есть коллективное колебание всего кристалла.

Так как нормальные колебания независимы, то энергию кристалла можно представить как сумму энергий отдельных нормальных осцилляторов:

, (13)

где n_j – число фононов (квантов возбуждения осциллятора) в состоянии с нормальной частотой , а суммирование ведётся по всем степеням свободы кристалла: j=1,2…3N_ат. Сумму (13) можно представить в виде суммы энергии основного состояния Е₀ и энергии возбуждённого состояния, т.е. тепловой энергии Е(Т):

, (14)

где энергия нулевых колебаний кристалла, а тепловая энергия есть суммарная энергия всех фононов кристалла

. (15)

Таким образом, в гармоническом приближении тепловая энергия кристалла есть сумма энергии всех фононов кристалла, а фонон с энергией есть квант возбуждения коллективного (нормального) колебания кристалла.

Между фононом и фотоном существует глубокая аналогия. В квантовой электродинамике электромагнитное поле (ЭМП) рассматривается как квантовая система с бесчисленным числом степеней свободы. Основное (невозбуждённое) состояние характеризуется нулевыми флуктуациями вакуума, а квантами возбуждения ЭМП являются фотоны, которым согласно квантово-корпускулярному дуализмому соответствуют электромагнитные волны. Кристалл представляет собой квантовую систему с очень большим (порядка или больше числа Авогадро, т.е. N>10²³) числом степеней свободы. Поэтому кванты возбуждения кристалла и различных его подсистем (решёточной, электронной, спиновой и т.д.) обладают свойством частиц: энергией, импульсом, спином и т.д. Их называют квазичастицами. В отличие от структурных частиц, образующих кристалл, атомных ядер и электронов, квазичастицы не могут покинуть кристалл, квантами возбуждения которого они являются. Современная физика твёрдого тела оперирует с несколькими видами квазичастиц: фононами, плазмонами, магнонами, поляронами, флуктуонами и т.д.

Фононы – кванты возбуждения коллективных колебаний атомов кристаллической решётки. В соответствие с квантово-корпускулярным дуализмом им соответствуют упругие волны смещения в кристалле

. (16)

С точностью до нормировочной постоянной упругая волна (16) является волновой функцией фонона. Представления о фононе были предложены И.Е. Таммом в 1931 г. по аналогии с фотоном как квантом возбуждения ЭМП.

Плазмоны – квазичастицы, являющиеся квантами возбуждения колебательной степени свободы электронной системы металла. Им соответствуют волны зарядовой плотности. Спиновым волнам в ферромагнетиках соответствуют магноны и т.д.

Представление о квазичастицах позволяет приближённо решить проблему многих тел – проблему описания системы большого числа сильновзаимодействующих частиц, электронов и ядер, образующих кристаллические материалы. Основное положение метода квазичастиц состоит в том, что реальный кристалл в условиях теплового, электромагнитного и других видах внешних воздействий моделируется как ящик с газом квазичастиц и для описания его физических свойств используется статистическая физика газов.