Глава 2. Колебания атомов кристаллической решётки

2.1. Гармоническое приближение

Динамика кристаллической решётки играет большую роль во многих областях физики твёрдого тела. Тепловое движение заставляет атомы (или ионы) решётки колебаться относительно своих положений равновесия. Возвращающими силами являются силы химической связи и/или силы Ван-дер-Ваальса.

Если сообщить энергию одному из ионов решётки, то в результате межатомного взаимодействия эта энергия распределится на всю решётку. Таким образом, возбуждение локального колебания приводит к коллективному колебанию атомов всего кристалла. Этот процесс полностью определяется потенциалом парного взаимодействия атомов кристалла U(R). Для любых типов связи эта функция имеет минимум в положении равновесия R=R₀; при R>R₀ преобладают силы притяжения, а при R<R₀ – силы отталкивания. Разложим в ряд Тейлора потенциал парного взаимодействия в окрестности положения равновесия:

(1)

При рассмотрении малых колебаний важную роль играет гармоническое приближение, в котором этот ряд ограничивают термом, содержащим вторую производную. Приближение, в котором учитывают производные более высокого ранга, называют ангармоническим.

Обозначим смещение атома из положения равновесия u=R–R₀, а потенциальную энергию относительно минимального значения W=U(R) – U(R₀) и учитывая, что в минимуме функции , получим

, (2)

а для возвращающей силы:

, (3)

где − жёсткость квазиупругой связи между атомами.

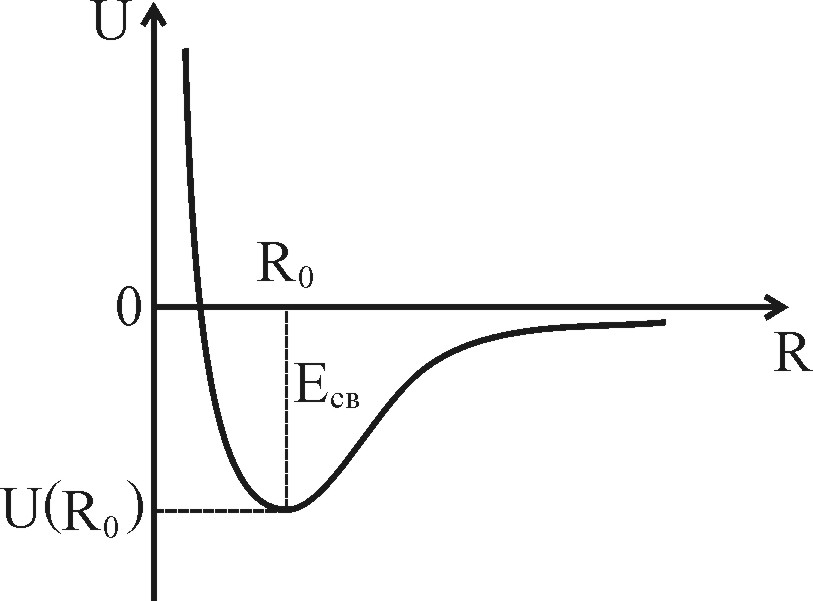
Рис. 2.1. Потенциала парного взаимодействия атомов кристалла

Таким образом, в гармоническом приближении взаимодействие атомов кристалла считается чисто упругим и соседние атомы можно моделировать шариками массой m, соединёнными упругими пружинами (Рис. 2.2).

Рис. 2.2. Модель взаимодействия атомов в кристалле

2.2. Колебания атомов одномерного кристалла с одним атомом в элементарной ячейке

Рассмотрим бесконечный одномерный одноатомный кристалл, т.е. цепочку атомов массой m, равновесные положения которых определяются вектором решётки , где n=1,2,3…N_ат, − параметр решётки. В гармоническом приближении связи между соседними атомами будем считать чисто упругими. При классическом рассмотрении при температуре Т=0 К атомы неподвижны и находятся в положении равновесия. При нагревании атомы начинают совершать тепловое движение (рис. 2.3.). Единственным типом движения в цепочке атомов с упругими связями могут быть упругие волны смещения атомов из положения равновесия:

, (1)

где k, и А – волновой вектор, циклическая частота и амплитуда упругой волны соответственно.

Рассмотрим силы, действующие на n-ый атом в одномерном кристалле в произвольный момент времени t.

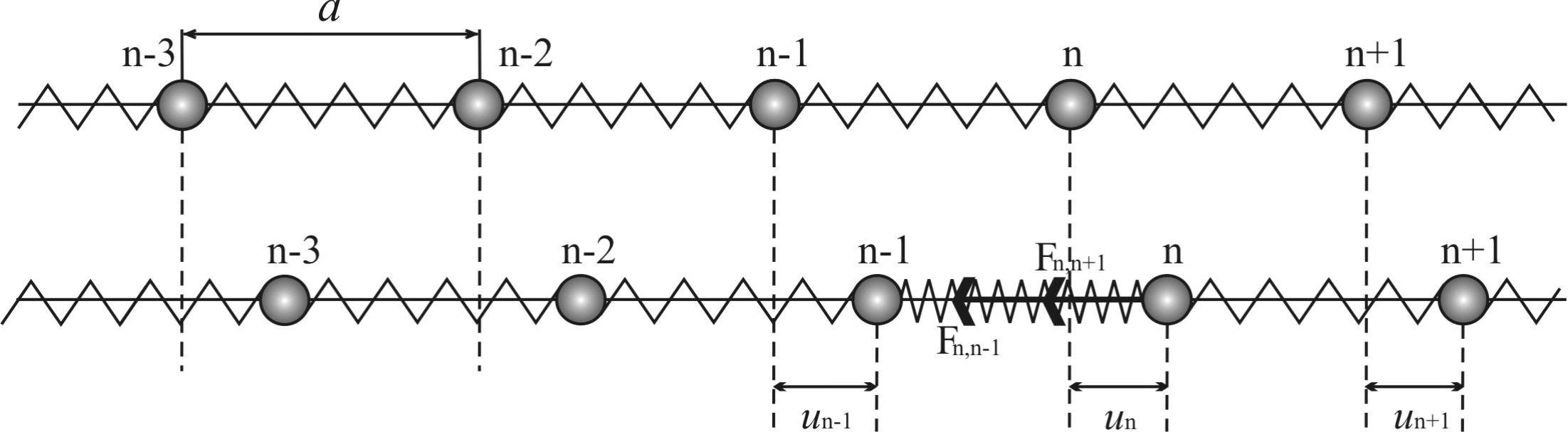
Рис. 2.3. Схема, поясняющая возникновение возвращающей упругой силы, которая действует на n-ый атом при его смещении из положения равновесия на расстояние u_n

Величина силы, действующей на n-ый атом со стороны (n+1)-ого атома есть , а со стороны (n − 1)-ого атома сила равна . Запишем уравнение движения n-ого атома

. (2)

Будем искать решение этого уравнения в виде упругой волны (1). Вычислим сначала ускорение n-ого атома: . Для смещения соседних атомов u_n+1 и u_n-1 соответственно имеем: . Подставляя эти выражения в уравнение (2), получим:

. (3)

Используя формулу Эйлера: , преобразуем (3) к виду

(4)

и окончательно:

, (5)

где – максимальная (предельная) частота в спектре колебаний атомов одномерного кристалла.

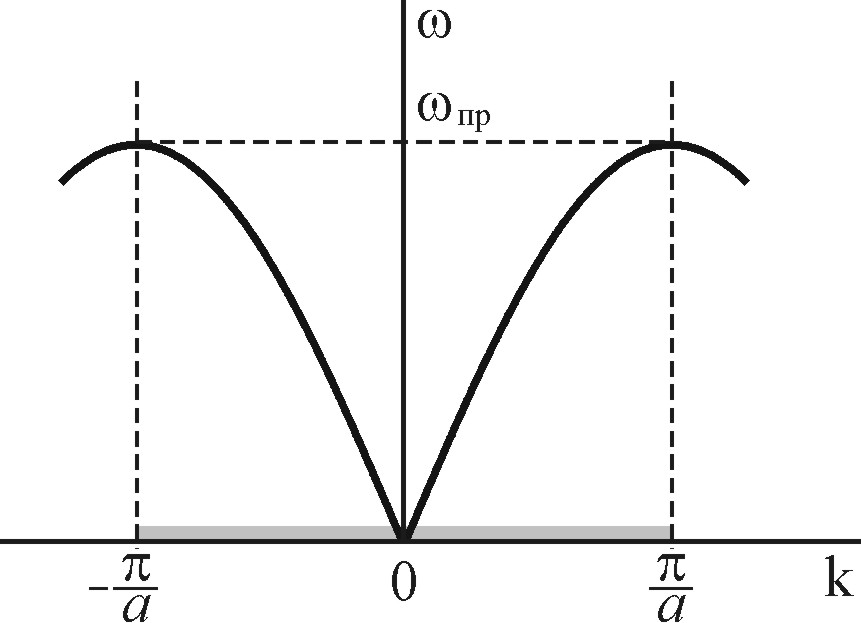
Зависимость частоты волны от волнового числа называется законом дисперсии. На рис. 2.4 показана зависимость периодической функции в первом периоде, (т.е. в интервале от до значений волнового числа), который называется первой зоной Бриллюэна. Обычно законы дисперсии волн строят в 1-ой зоне Бриллюэна, так как она содержит все физически различные значения волнового числа k.

Рис. 2.4. Закон дисперсии акустических волн в одномерном одноатомном кристалле

Скорость передачи упругих взаимодействий определяется групповой скоростью . Из волновой физики известно, что

.

В одномерном случае очевидно Дифференцируя по k закон дисперсии (5), получим зависимость групповой скорости акустических волн от волнового числа

. (6)

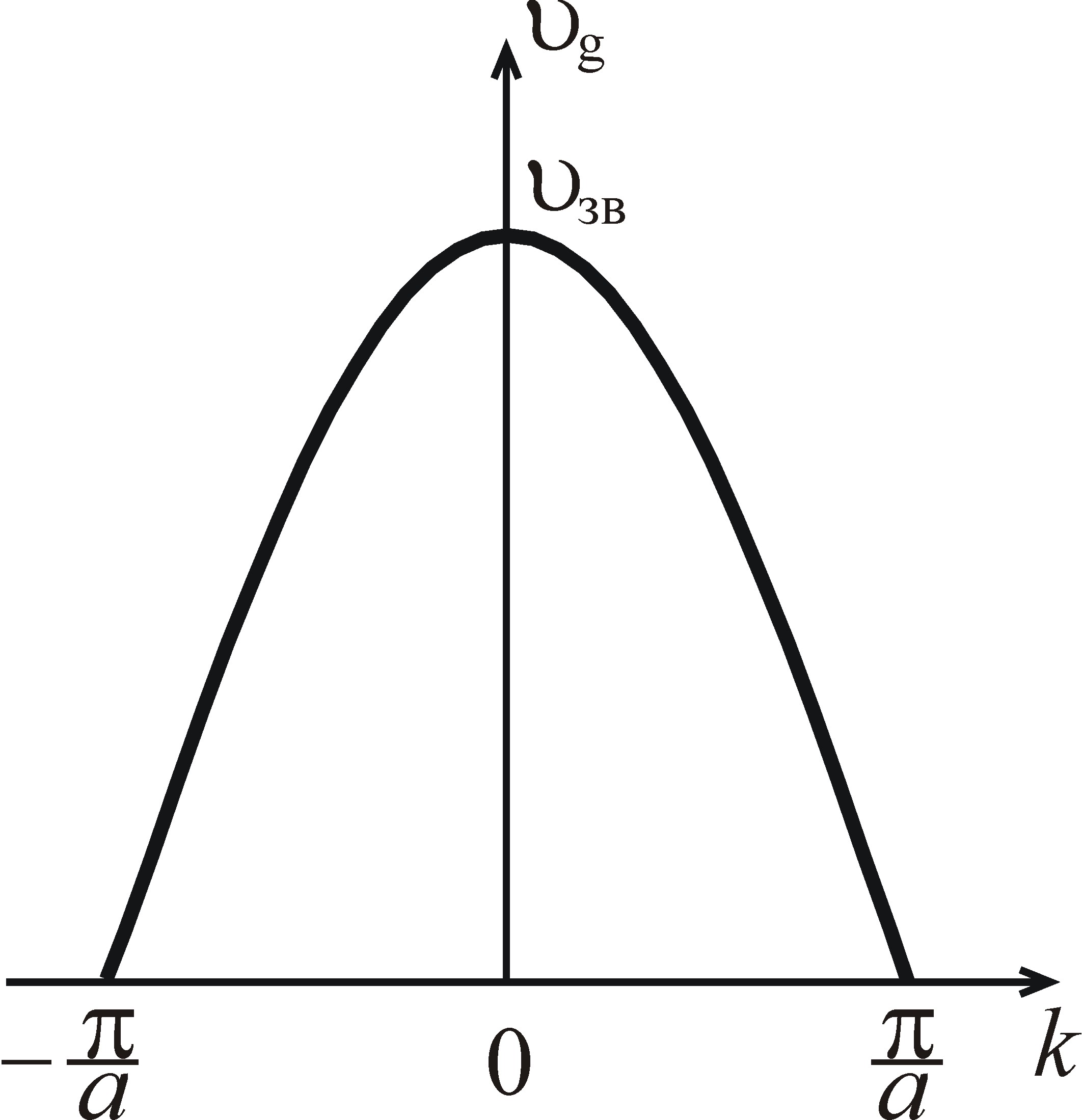
Рис. 2.5. Зависимость групповой скорости акустических волн в одномерном кристалле от волнового числа

Максимальное значение групповой скорости приходится на центр 1-ой зоны Бриллюэна, когда и , т.е. на длинноволновую область спектра. Длинноволновые возбуждения можно рассматривать как упругие волны в непрерывной среде, когда дискретностью кристалла можно пренебречь. Скорость упругих волн (скорость звука) определяется в механике следующим выражением: , где Е – упругий модуль Юнга, − плотность среды. Модуль Юнга, по определению, есть отношение силы к вызванной ей относительной деформации, т.е. . Плотность одномерного одноатомного кристалла , поэтому в одномерном случае . С учётом этого перепишем (6) в виде

(7)

Рассмотрим закон дисперсии акустических колебаний в области длинных и коротких волн.

Длинные волны: .

В этом случае и функцию можно приближенно заменить аргументом, т.е.

. (8)

Таким образом, в длинноволновой области закон дисперсии акустических волн линеен по волновому числу k, а групповая скорость, как ожидалось, равна скорости звука .

Короткие волны:

Так как кристалл представляет собой дискретную среду, то существует минимальная длина волны смещения атомов из положения равновесия , когда соседние атомы колеблются в противофазе, т.е. . Эта ситуация соответствует стоячей волне и групповая скорость равна нулю, . Соответствующее минимальной длине волны волновое число очевидно равно . Таким образом, на границах первой зоны Бриллюэна, длина волны имеет минимальное значение , а циклическая частота достигает максимального значения в соответствии с законом дисперсии (5).

Условие на границе зоны Бриллюэна аналогично закону Вульфа-Брэгга для одномерного кристалла. Действительно, согласно закону Вульфа-Брэгга связь между длиной волны излучения , углом скольжения и межплоскостным расстоянием d определяется условием интерференционных максимумов: . В одномерном случае надо принять , d=a, тогда для главного максимума, т.е. при n=1, получим , что и соответствует волновому числу . Таким образом, на границе зоны Бриллюэна соблюдается закон Вульфа-Брэгга, т.е. происходит брэгговское отражение упругой волны смещения. При приближении волнового числа k к границе зоны Бриллюэна возникает интерференция падающей и отражённых волн. Длина волны в этой области соизмерима с межатомным состоянием и кристалл является дифракционной решёткой для акустической волны. Из-за интерференции падающей и отражённой волн групповая скорость монотонно уменьшается с ростом k и обращается в нуль на границе зоны Бриллюэна, когда .