Глава 1. Трансляционная симметрия кристалла

Кристаллическая решетка характеризуется периодическим расположением атомов в трех измерениях. Пространственная периодичность атомов в идеальном (бездефектном) кристалле объясняется тем, что равновесие сил притяжения и отталкивания между атомами, соответствующее минимуму потенциальной энергии системы достигается при условии трехмерной периодичности. Для описания кристаллической решетки достаточно знать размещение атомов в ее элементарной ячейке, повторением которой путем параллельных переносов (трансляций) образуется кристаллическая решетка. В общем случае элементарная ячейка имеет форму косоугольного параллелепипеда (Рис. 1.1.).

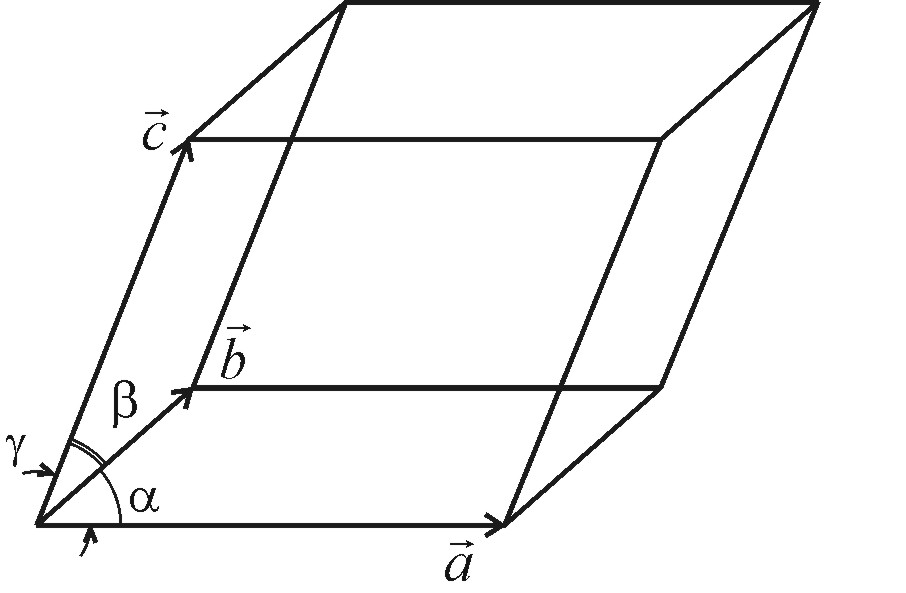
Рис. 1.1. Элементарный параллелепипед

Однако построить кристалл можно трансляцией различных параллелепипедов. Согласно О. Браве элементарной ячейкой будет служить тот параллелепипед, который удовлетворяет следующим условиям: 1) симметрия элементарной ячейки должна соответствовать симметрии кристалла; 2) число прямых углов между ребрами должно быть максимальным; 3) при соблюдении первых двух условий объем ячейки должен быть минимальным.

Примитивной элементарной ячейкой называется ячейка, в которой узлы решетки расположены в вершинах параллелепипеда, образующих ячейку. Положение любого узла в решетке определяется вектором решетки

,

где  целые числа,  базисные векторы решетки (Рис. 1.1). Модули векторов , т.е. величины и углы между векторами – называются параметрами решетки.

Элементарные ячейки различают на простую (P), базоцентрированную (C), объемноцентрированную (J) и гранецентрированную (F). В простой (примитивной) ячейке узлы кристаллической решетки расположены в вершинах параллелепипеда, образующего ячейку. Если узлы находятся не только в вершинах параллелепипеда, но и в центре его оснований, то решетка называется базоцентрированной. В объемноцентрированной имеется дополнительный узел в месте пересечений пространственных диагоналей, а в гранецентрированной узлы находятся в центре всех боковых граней. Типы элементарных ячеек представлены на рис. 1.2.

По форме элементарных ячеек в зависимости от соотношения между величинами ребер и углов между гранями различают семь кристаллических систем (сингоний): триклинную, моноклинную, ромбическую, тетрагональную, гексагональную, ромбоэдрическую и кубическую (см. Таблицу 1.1.).

Эти системы имеют следующие свойства:

1. Триклинная: , . Ни одна из кристаллических осей не перпендикулярна какой-либо другой, а периоды трансляции различны для всех трех осей.

2. Моноклинная: , =90º . Две кристаллические оси не перпендикулярны друг другу, но третья перпендикулярна им обеим. Периоды трансляции различны вдоль всех трех осей. Моноклинные решетки могут быть простыми или базоцентрированными.

Рис. 1.2. Типы элементарных ячеек

Таблица 1.1.

Кристаллические сингонии	Соотношения между сторонами и углами	Номер решетки на рис. 1.3.	Решетки Браве
Триклинная	, 90°	1	Объемноцентрированная 7,9,14 Гранецентрированная 3,6,13 Базоцентрированная 5
Моноклинная	, =90º	2,3
Ромбическая	=90°	4,5,6,7
Тетрагональная	, =90º	8,9
Гексагональная	, =90º 120º	10
Ромбоэдрическая	90º	11
Кубическая	, =90º	12,13,14

3. Ромбическая: , =90º. Кристаллические оси взаимно перпендикулярны, но периоды трансляции вдоль всех трех осей различны. Ромбические решетки могут быть простыми, базоцентрированными, объемноцентрированными или гранецентрированными.

4. Тетрагональная: , =90º. Кристаллические оси взаимно перпендикулярны. Периоды трансляции вдоль двух осей одинаковы, но вдоль третьей оси период имеет другое значение. Тетрагональные решетки могут быть простыми или объемноцентрированными.

5. Гексагональная: , =90º, 120º . Угол между двумя кристаллическими осями составляет 60°, в то время, как третья ось перпендикулярна им обеим. Периоды трансляции одинаковы для осей, разделенных углом 60°, но вдоль третьей оси период имеет другое значение.

Гексагональной система называется потому, что из таких ячеек можно образовать простую гексагональную структуру. Обычно удобнее рассматривать гексагональную структуру с помощью единичной элементарной гексагональной ячейки, которая имеет четыре оси, три из которых, образуя между собой углы 120°, лежат в одной плоскости, а четвертая ось перпендикулярна этой плоскости. Период трансляции один и тот же для трех компланарных осей, но имеет другое значение для четвертой оси.

6. Ромбоэдрическая: , 90º (иногда называемая тригональной). Углы между каждой парой осей одинаковы, но не равны 90°. Периоды трансляции одинаковы по всем трем осям.

7. Кубическая: , =90º. Кристаллические оси взаимно перпендикулярны, а интервал повторения (период трансляции) один и тот же вдоль всех трех осей. Кубические решетки могут быть простыми, объемноцентрированными и гранецентрированными.

В 1848 г. О. Браве показал, что все разнообразие кристаллических структур можно описать с помощью 14 типов элементарных решеток: решетки P, J, F кубической сингонии, P, C, J, F ромбической сингонии, P, J и P, C тетрагональной и моноклинной сингонии и P гексагональной, тригональной и

Рис. 1.3. Решетки Браве: триклинная (1), моноклинная (2), моноклинная гранецентрированная (3), ромбическая (4), ромбическая базоцентрированная (5), ромбическая гранецентрированная (6), ромбическая объемноцентрированная (7), тетрагональная (8), тетрагональная объемноцентрированная (9), гексагональная (10), ромбоэдрическая (11), кубическая (12), кубическая гранецентрированная (13), кубическая объемноцентрированная (14)

триклинной сингоний. Эти решетки называются решетками Браве (рис.1.3.).

Последние представляют собой такие трехмерные наборы точек, в которых каждая точка окружена своими соседями совершенно одинаковым образом. В простейших кристаллах в каждой точке решетки находится по одному атому, но часто каждый узел решетки занимают группы из двух или большего числа атомов, причем каждая группа одинакова по составу, расположению и ориентации. Следовательно, есть различие между структурой кристалла, представляющей собой реальное расположение в пространстве составляющих кристалл атомов, ионов или молекул, и соответствующей кристаллической решеткой, являющейся абстрактным геометрическим образом, полезным при классификации кристаллов.