8.1.3. Циклотронный резонанс в металлах
Циклотронный
резонанс – явление резонансного
поглощения высокочастотной электромагнитной
волны микроволнового диапазона металлом
или полупроводником, помещенным во
внешнее однородное магнитное поле.
Условием резонанса является равенство
циклотронной частоты и частоты
микроволнового поля
.
Происхождение
термина «циклотронный» связано с тем,
что в циклотроне частицы (положительные
ионы) ускоряют, прикладывая к электродам
или дуантам, радиочастотные импульсы
с частотой
.
Частицы непрерывно обращаются по
окружности, получая ускорение каждый
раз, когда они проходят между дуантами.
В опытах по циклотронному резонансу
электронов подобный метод используется
для ускорения электронов в переменном
высокочастотном (микроволновом)
электрическом поле, которое прикладывается
в плоскости, перпендикулярной однородному
магнитному полю
.
При этом электроны ускоряются как в
циклотроне, но ускорение наблюдается
не путем непосредственного наблюдения
частиц, а косвенно, по поглощению
микроволнового поля на циклотронной
частоте
.
Явление циклотронного резонанса в металлах было теоретически предсказано в 1956 г. М.Азбелем и Э.Канером и потому носит их имя. Экспериментально циклотронный резонанс впервые наблюдал Е. Фоусетт на олове в 1956 г.
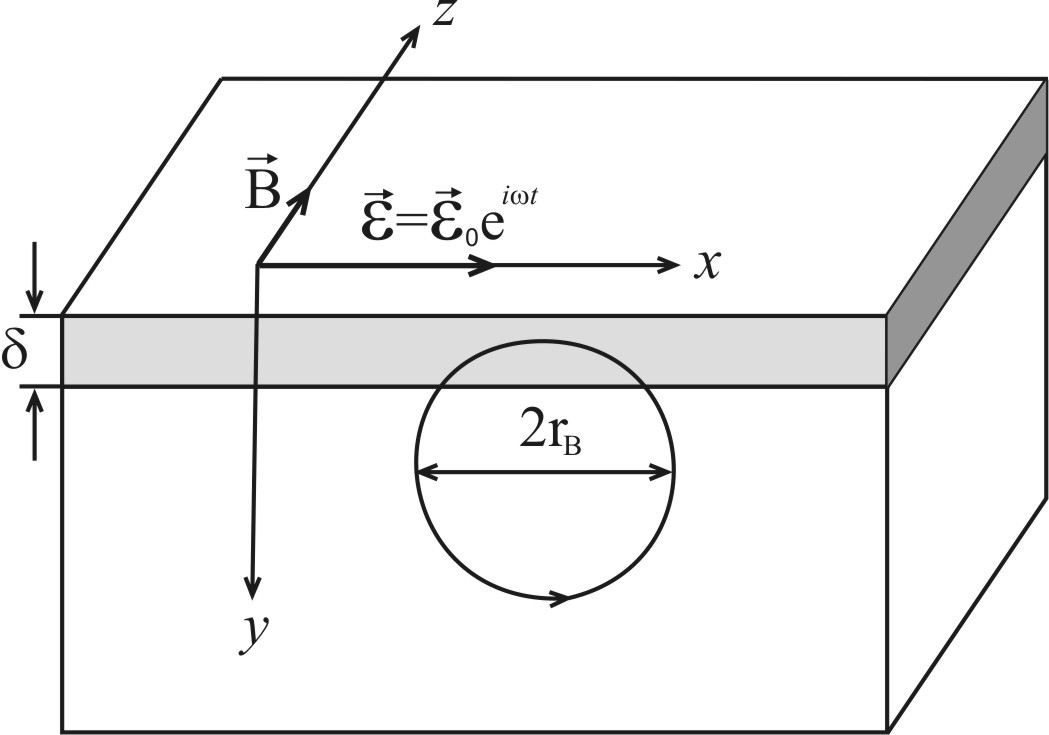
Рис. 8.3. Расположение внешних однородного
магнитного и переменного электрического
полей для наблюдения циклотронного
резонанса. d – толщина
скин-слоя.
Внешнее однородное магнитное поле было направлено параллельно поверхности монокристалла, а вектор переменного электрического поля в линейно поляризованной электромагнитной волне был перпендикулярен вектору и расположен также параллельно поверхности кристалла. Такое взаимное расположение внешних полей к поверхности кристалла получило название геометрии Азбеля-Канера (Рис. 8.3.).
Из электродинамики известно, что электромагнитное поле проникает в металл на конечную глубину, равную толщине скин-слоя:
,
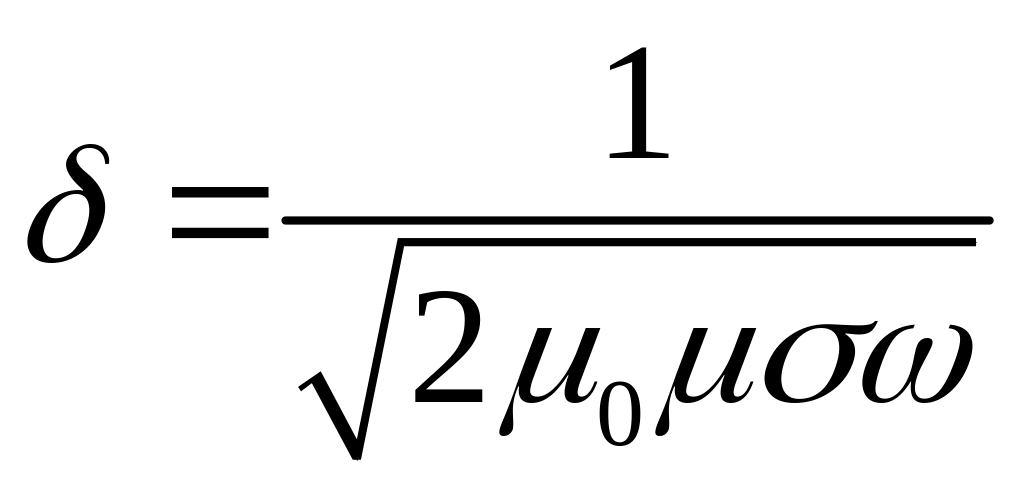(17)
где
–
магнитная проницаемость вакуума,
– магнитная проницаемость металла. В
высокочастотных полях
.
Полагая
ГГц,
Ом-1м-1,
получим оценку
м. Такое
значение на несколько порядков превосходит
длину свободного пробега при комнатной
температуре
м.
Таким образом, соблюдается условие
нормального скин-эффекта
,
когда все электроны вблизи уровня Ферми
эффективно взаимодействуют с внешним
микроволновым полем. Но в этом случае
не может наблюдаться циклическое
движение электронов во внешнем поле.
Для циклотронного резонанса необходимо
соблюдение двух условий:
,
(18)
из которых следует,
что циклотронный резонанс наблюдается
в области аномального
скин-эффекта,
когда длина свободного пробега электронов
значительно превышает глубину
проникновения микроволнового поля,
т.е.
.
В этом случае скин-слой исполняет роль
дуанта в циклотроне. Попадая в скин-слой
при циклическом движении электрон
ускоряется, получая энергию микроволнового
поля (Рис. 8.3.).
Условия (18)
выполняются на совершенных
монокристаллических образцах металлов,
помещенных в магнитное поле с индукцией
~1 Тл при гелиевых температурах. Резонансное
ускорение электрона имеет место в том
случае, если электрон возвращается в
скин-слой и взаимодействует с
электромагнитной волной в течении
интервала времени
при одной и той же фазе электрического
поля. Для этого необходимо, чтобы период
циклического
движения электрона в целое число раз
превосходил период
колебаний поля волны, т.е.
,
где
называют индексом резонансной гармоники.
Для регистрации
циклотронного резонанса образец металла
помещают в катушку колебательного
контура или внутрь СВЧ-резонатора,
настроенного на частоту
.
При совпадении частоты
с
уменьшение полного сопротивления
(при резонансе действительная
и мнимая
части полного поверхностного импеданса
равны) приводит к уменьшению затухания,
которое вносит образец металла в
резонатор, в результате чего возрастают
добротность резонатора и амплитуда
электромагнитных колебаний.
Циклотронный резонанс дает метод измерения эффективной массы электрона. В соответствии с теорией циклотронного резонанса Азбеля-Канера для металлов с произвольным законом дисперсии путем изменения направления магнитного поля относительно кристаллографических осей образца можно определить экстремальные значения циклотронных масс, относящихся к различным сечениям поверхности Ферми и построить форму этой поверхности.