7.3.2. Электропроводность легированных полупроводников

Электропроводность слаболегированных полупроводников будет складываться из электропроводности собственного полупроводника и электропроводности, связанной с избыточной концентрации носителей, поставляемых донорной (или акцепторной) примесью.

. (26)

Поскольку энергия ионизации донорной (акцепторной) примеси значительно меньше ширины запрещенной зоны, то с ростом температуры сначала термолизуются мелкие центры и проводимость будет определяться, в основном, их концентрацией в кристалле. При некоторой температуре, называемой температурой насыщения, вся примесь термолизуется и уже не будет поставлять носители заряда в зоны. При дальнейшем росте температуры рост электропроводности будет определяться собственной проводимостью (первым слагаемым в (26)).

При увеличении концентрации примеси примесные уровни расщепляются в примесные зоны в соответствии с общими представлениями зонной теории (см. метод сильной связи). Если уровень Ферми находится в такой примесной зоне, то возникает проводимость в примесной зоне без участия зонных электронов и дырок. По мере увеличения концентрации примеси сначала оказывается возможным механизм прыжковой проводимости за счет туннелирования электронов от одного примесного центра к другому, а при дальнейшем росте концентрации происходит так называемый переход Андерсона, состоящий в спонтанном образовании делокализованных электронных состояний. Распределение электронной плотности таких делокализованных состояний и линии тока имеют сложную лабиринтную (фрактальную) структуру и описываются с помощью теории перколяции.

Глава 8. Методы исследования электронной структуры металлов и полупроводников

Экспериментальные методы исследования зонной структуры металлов и полупроводников в основном базируются на изучении различных физических эффектов в этих кристаллах, происходящих в присутствии внешнего магнитного поля. Эти методы можно разделить на гальваномагнитные, связанные с измерением электропроводности металла и эффекта Холла в слабых и сильных магнитных полях и квантовые осцилляционные эффекты в сильных (квантующих) магнитных полях, проявляемые как осцилляций различных кинетических коэффициентов (проводимости, магнитной восприимчивости и т.д.) в растущем магнитном поле.

8.1. Гальваномагнитные методы и циклотронный резонанс

8.1.1. Эффект Холла

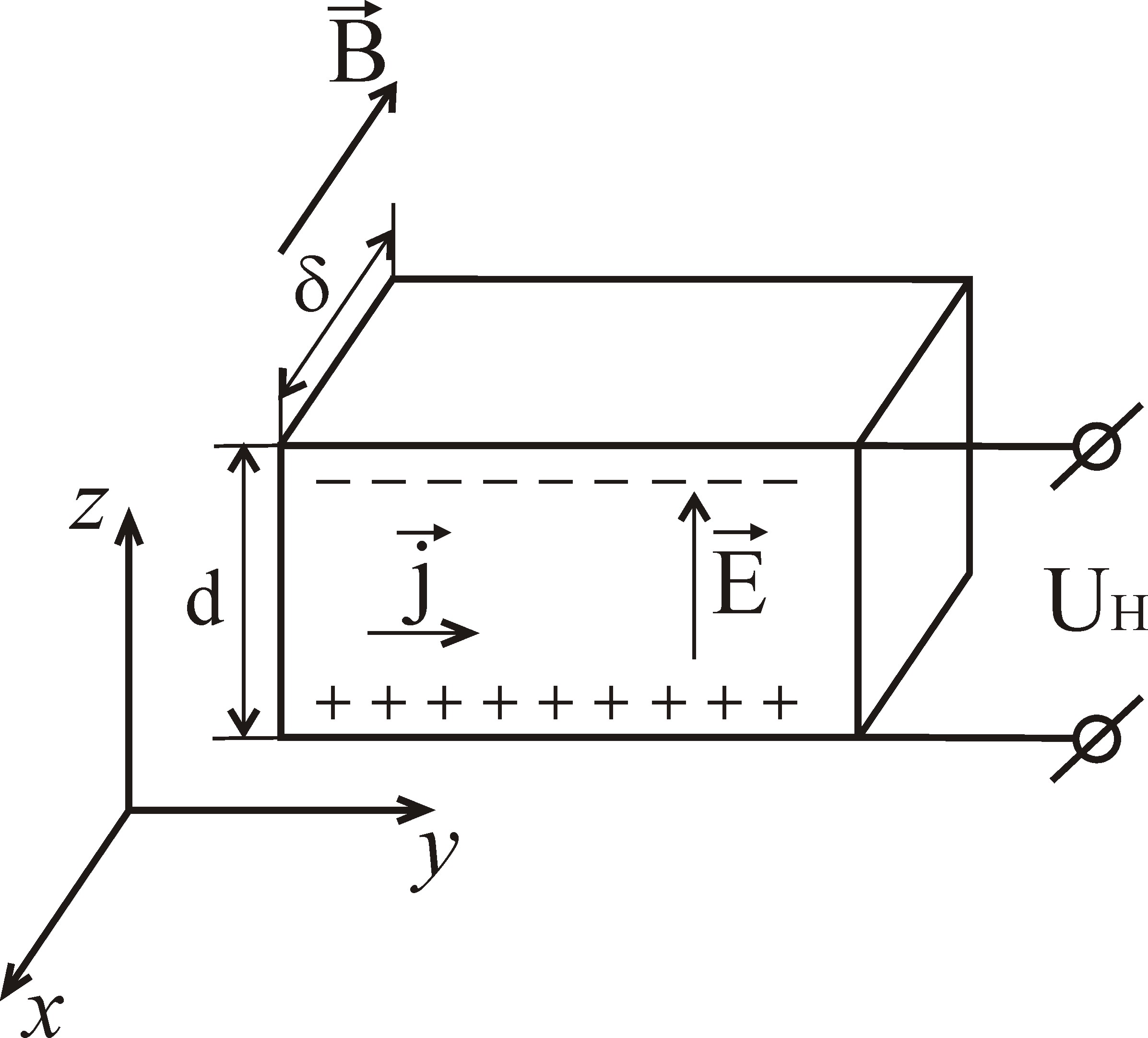
Наиболее простым и важным для физики металлов и полупроводников является эффект Холла в слабых магнитных полях. Сущность эффекта заключается в следующем. Проводник с током помещают в магнитное поле с вектором индукции, направленным перпендикулярно току (Рис. 8.1.)

Рис. 8.1. Схематическое изображение проводника с током в магнитном поле для измерения холловского напряжения

В магнитном поле на движущиеся носители заряда будет действовать сила Лоренца , перпендикулярная вектору скорости и вектору магнитной индукции . Дрейфовая скорость электронов направлена против поля, т.е. в направлении y, поэтому сила Лоренца, действующая на отрицательные заряды (электроны) направлена в положительном направлении оси z. По мере того, как электроны скапливаются на верхней границе проводника, будет нарастать электрическое поле, противодействующее движению и дальнейшему накоплению электронов.

Разделение зарядов в направлении оси z будет происходить до тех пор, пока сила Лоренца не уравновесится противоположно направленной кулоновской силой . В одномерном случае (разделение зарядов происходит вдоль оси z) соответственно имеем:

,

где – угол между векторами и . В результате разделения зарядов устанавливается постоянная (при данных значениях магнитной индукции и токе I) разность потенциалов между верхней и нижней поверхностью кристалла , называемая холловской разностью потенциалов или холловским напряжением. Очевидно , где E – напряженность холловского электрического поля, – размер проводника вдоль оси . Измеряемый в эксперименте ток есть , где – размер проводника вдоль оси

(в направлении магнитного поля ). Плотность тока связана с дрейфовой скоростью известным из электродинамики соотношением:

, (2)

где n – концентрация носителей заряда. С учетом (1) и (2) для холловской разности потенциалов получим:

, (3)

Постоянную называют постоянной Холла. Постоянная Холла несет информацию о знаке и концентрации носителей заряда в полупроводнике или металле.