7.2. Проводимость собственных полупроводников

Электропроводность полупроводника складывается из электронной и дырочной электропроводности . В квазиклассическом приближении электропроводность определяется выражением вида формулы Друде-Лоренца, в которой масса электрона заменена на эффективную массу m^*, т.е.

. (19)

Умножая числитель и знаменатель на скорость носителя заряда, получим, например, для электронной проводимости

. (20)

Так как электроны в зоне проводимости полупроводника образуют классический газ, подчиняющийся статистике Максвелла-Больцмана, то средняя скорость теплового движения “классических” электронов будет расти с температурой как , что следует непосредственно из равенства . Равновесная концентрация электронов зависит от температуры в соответствии с выражением (16), т.е. как . Поэтому в отличие от металла, где от температуры зависит, главным образом, только длина свободного пробега электрона l(T), в собственном полупроводнике от температуры также сильно зависят и концентрация n(T) и скорость электронов.

Так как дно зоны проводимости в соответствии с законом дисперсии соответствует центральной области 1-ой зоны Бриллюэна, то есть длинноволновым электронам, то их импульсы находятся вдали от границ зоны Бриллюэна , поэтому в широком температурном диапазоне соблюдается условие рассеяния электрона на фононе, так как . Как было показано в теории металлов, если каждое электрон-фононное взаимодействие приводит к рассеянию электрона, то при температурах выше дебаевской обратно пропорциональна температуре длина свободного пробега электрона . Таким образом, температурные зависимости концентрации , средней скорости теплового движения и средней длины свободного пробега электрона в собственном полупроводнике имеют следующий функциональный вид:

,

, (21)

.

Подставляя эти формулы в выражение для электропроводности (20), получим

, (22)

где – постоянная, соизмеримая с проводимостью металла, что соответствует термолизации большинства электронов валентной зоны в зону проводимости, то есть гипотетической ситуации бесконечно высоких температур. Постоянную определяют обычно экспериментально.

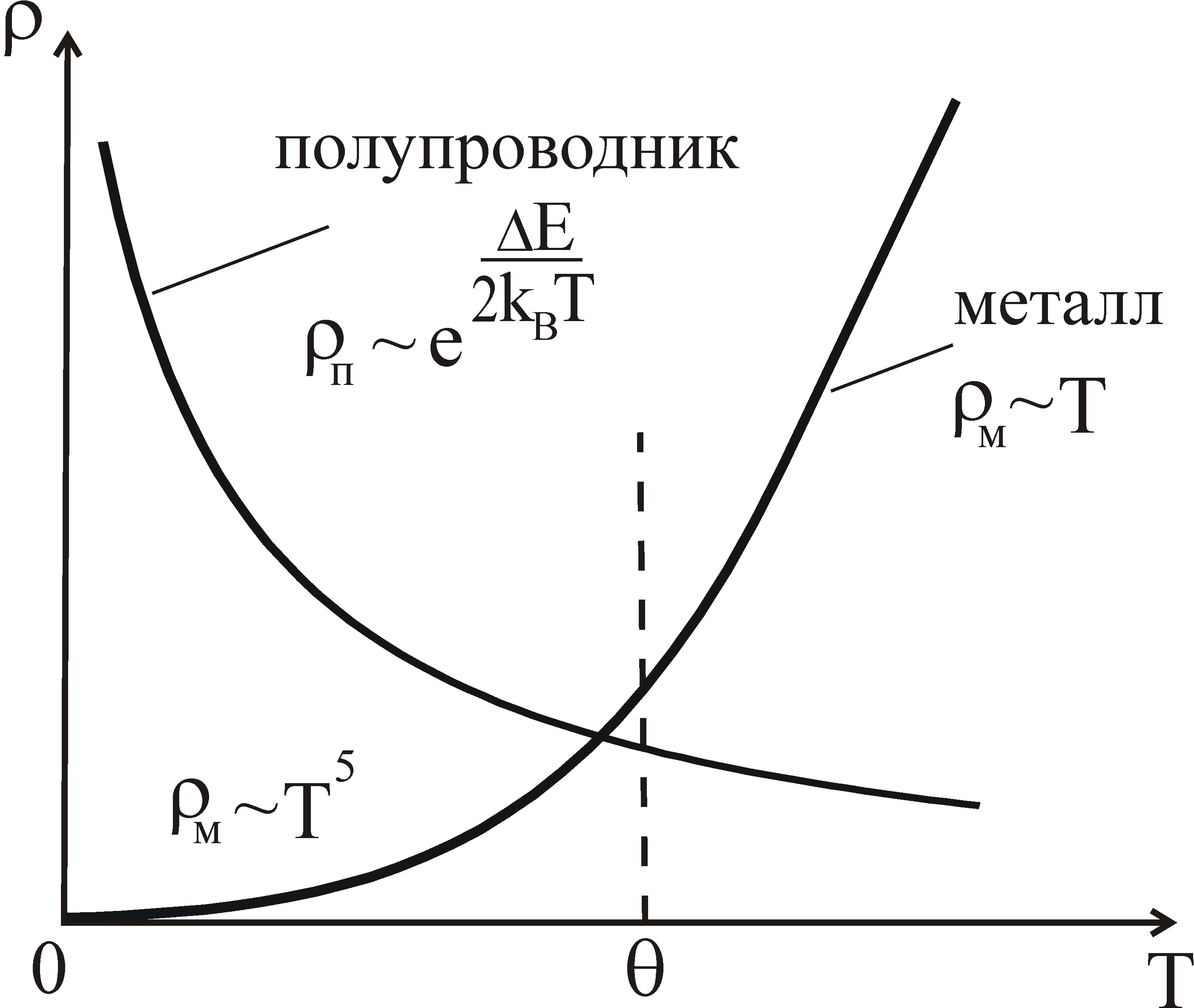
Рис. 7.3. Сравнение температурных зависимостей удельного сопротивления полупроводника и нормального металла

На рис. 7.3 показана температурная зависимость удельного сопротивления собственного (беспримесного) полупроводника в сравнении с аналогичной зависимостью для бездефектного нормального металла. Рисунок демонстрирует основное качественное отличие металла от полупроводника: при любой температуре температурный коэффициент сопротивления положительный для металла и отрицательный для полупроводника.

7.3. Проводимость легированных полупроводников

7.3.1. Элементарная теория мелких центров

При легировании полупроводника иновалентной примесью с валентностью, на единицу отличающуюся от валентности атомов кристаллической матрицы, образуются однозарядные центры положительные (или отрицательные), которые образуют водородоподобные системы с электронами (или дырками). Соответственно в кристалле полупроводника образуются донорные (или акцепторные) центры, которые при термическом или фотовозбуждении поставляют: донорные центры – электроны в зону проводимости; акцепторные центры – дырки в валентную зону.

В качестве примера донорного центра в полупроводнике рассмотрим кристалл кремния Si, в котором один узел решетки занят атомом фосфора P. Атом фосфора находится в пятой группе периодической системы и имеет максимальную валентность равную пяти за счет sp³-гибридизации электронов внешней оболочки. Фосфор образует раствор замещения в кристаллической решетке кремния, имеющей координационное число равное четырем. Поэтому четыре валентных электрона атома фосфора образуют ковалентные связи с соседними атомами кремния, а “лишний” электрон образует водородоподобную систему с однозарядным ионом фосфора

В отличие от атома водорода электрон движется в среде с высокой диэлектрической проницаемостью (для монокристалла кремния ). Поэтому сила кулоновского притяжения электрона к центру будет в раз меньше, чем в атоме водорода при равных расстояниях до центра. Это приводит и к существенному увеличению радиуса первой боровской орбиты. В атоме водорода радиус первой боровской орбиты . Соответствующий радиус для донорного центра будет приблизительно в раз больше и объем области движения электрона, с учетом асимптотического поведения радиальной волновой функции, превысит объем элементарной ячейки кристалла. Поведение электрона в периодическом поле кристалла описывается методом эффективных масс. Таким образом, для расчета энергетического спектра донорного центра можно использовать спектр энергии водородоподобного атома

, (23)

в котором массу электрона необходимо заменить на эффективную массу m_e. Необходимо также учитывать, что электрон движется не в вакууме с , а в полярной среде с проницаемостью , тогда для однозарядного (Z=1) донорного центра получим:

.

(24)

Рис. 7.4. Образование мелких уровней в запрещенной зоне полупроводника при легировании донорной и акцепторной примесью

Учитывая, что ,  эВ, получим для энергии ионизации донорного центра  эВ, что составляет около 8% ширины запрещенной зоны кремния  эВ. Поэтому такой донорный центр называют мелким: он расположен вблизи потолка запрещенной зоны на расстоянии от дна зоны проводимости E_c (рис. 7.4).

Акцепторный центр образуется при легировании кремния атомами из третьей группы периодической системы, например, атомами галия Ga. Для образования четырех ковалентных связей с соседними атомами кремния Si, атому галия помимо трех валентных электронов необходим еще один электрон. В результате в узле решетки появится однозарядный отрицательный центр , который образует водородоподобную систему с дыркой. Энергия связи дырки с центром Ga ^– и ее возбужденное состояние определяется формулой вида (24) с заменой эффективной массы электрона на эффективную массу дырки

. (25)

Соответствующие уровни называются акцепторными. Они располагаются в запрещенной зоне и отсчитываются от потолка валентной зоны E_V. При термическом возбуждении электроны вблизи потолка валентной зоны переходят на акцепторные уровни, при этом в валентной зоне появляются свободные носители – дырки. Этот процесс можно рассматривать как делокализацию дырки, то есть переход дырки из локального акцепторного уровня в валентную зону, где дырки делокализованы, то есть описываются блоховскими волнами, распространяющиеся по всему кристаллу.

При легировании кремния донорной примесью создается полупроводник с избытком электронов – полупроводник n-типа, а при легировании акцепторной примесью создается полупроводник p-типа, то есть содержащий избыток дырок. Получение кристаллов с заданным типом проводимости и гетероструктур, содержащих p-n-переходы, составляют основу современной микроэлектроники.