7.1.2. Статистика носителей заряда в полупроводниках

Электроны являются фермионами и подчиняются статистике Ферми-Дирака. Функция распределения Ферми-Дирака:

, (6)

где уровень Ферми E_f , по определению, есть уровень, вероятность заполнения которого равна 0.5. Поэтому уровень Ферми в собственных (т.е. беспримесных) полупроводниках находится в центре запрещенной зоны.

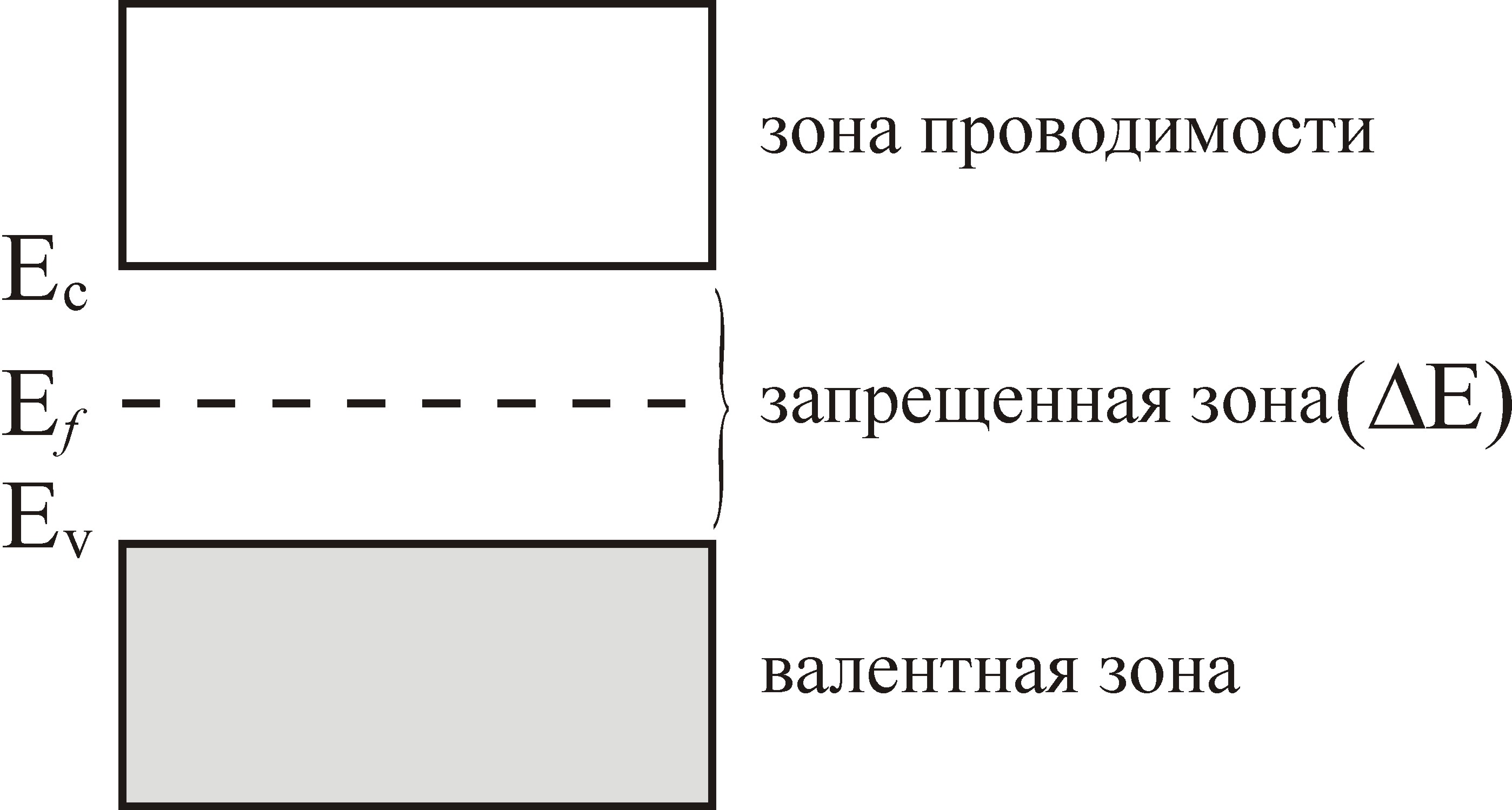
Рис. 7.2. Схема расположения уровня Ферми в собственном полупроводнике.

Энергия электрона вблизи дна зоны проводимости отдалена от уровня Ферми на величину, приблизительно равную половине ширины запрещенной зоны, то есть  эВ. Эта энергия значительно превышает среднюю энергию теплового движения при комнатной температуре  эВ. Поэтому отношение , а и в знаменателе формулы (6) можно пренебречь единицей. Тогда функция распределения Ферми-Дирака переходит в классическую функцию распределения Максвелла-Больцмана

. (7)

Функция определяет вероятность заполнения уровня E при абсолютной температуре T. Функцию распределения дырок можно определить как вероятность отсутствия электрона на уровне E, т.е.

(8)

Энергия дырки приблизительно равна потолку валентной зоны, то есть , поэтому и , и этой величиной можно пренебречь по сравнению с единицей, тогда функция распределения дырок также будет описываться классической функцией распределения Максвелла-Больцмана

. (9)

Таким образом, свободные носители заряда в полупроводнике – электроны в зоне проводимости и дырки в валентной зоне – образуют классический газ. Физический смысл этого утверждения состоит в низкой концентрации носителей в полупроводниках по сравнению с концентрацией электронов проводимости в металлах. Вследствие высокой концентрации электронов в металлах ( см^-3) обменное взаимодействие электронов приводит к запрету заполнения одного квантового состояния двумя и более электронами, что в свою очередь приводит к квантовому статистическому распределению Ферми-Дирака.

7.1.3. Равновесная концентрация электронов и дырок

в собственных полупроводниках

Носители заряда в полупроводниках, электроны и дырки, являются фермионами (частицами с полуцелым спином) и по закону сохранения углового момента они рождаются и уничтожаются (рекомбинируют) парами. При термическом возбуждении рождается электронно-дырочная пара: электрон в зоне проводимости и дырка в валентной зоне. С некоторой вероятностью происходит обратный переход, состоящий в рекомбинации пары электрон-дырка. В результате в зоне проводимости и валентной зоне полупроводника устанавливается равновесная концентрация электронов n_e и дырок n_p соответственно. В собственном полупроводнике концентрация свободных электронов и дырок очевидно равны, то есть .

Вычислим равновесную концентрацию электронов в зоне проводимости. Обозначим через dN – число электронных состояний с энергиями от E до E+dE. Число электронов в этом участке спектра очевидно равно , где f_e(E) есть вероятность заполнения уровня E, а двойка учитывает принцип Паули, т.е., что на каждом занятом уровне можно расположить по два электрона с противоположными спинами. Вводя далее функцию плотности состояния энергетического спектра электронов , получим выражение для концентрации электронов в зоне проводимости

. (10)

Здесь интегрирование ведется по зоне проводимости. Поскольку в полупроводнике электроны проводимости находятся вблизи дна зоны , то верхний предел можно принять бесконечно большим. Статистическая функция распределения есть распределение Максвелла-Больцмана (см. (7)), а плотность распределения D(E) определяется законом дисперсии электронов проводимости (см. (3)).

.

Квадратичный закон дисперсии означает, что изоэнергетическая поверхность в P-пространстве есть сфера, центр которой совпадает с центром 1-ой зоны Бриллюэна, P=0. Внутри сферы радиусом P находятся квантовые состояния с энергиями . Число состояний с энергиями от 0 до E обозначим через N. Очевидно, N равно отношению объема P-пространства, ограниченного этой сферой, то есть , к объему P-пространства, приходящегося на одно квантовое состояние , где V – объем кристалла, т.е.

.

Используя закон дисперсии электронов (3^), получим зависимость N(E) в виде:

(11)

Дифференцируем это выражение по энергии и получим функцию плотности состояния спектра электронов:

. (12)

Для вычисления концентрации электронов в зоне проводимости подставим (12) и (7) в выражение для концентрации (10):

. (13)

Представляя далее разность энергий E – E_f как , получим:

(14)

Введем новую переменную :

. (15)

Учитывая, что собственный интеграл в правой части равен , окончательно получим

(16)

для концентрации электронов в зоне проводимости.

Аналогичное выражение получается и для дырок в валентной зоне:

. (17)

Так как в собственном полупроводнике концентрация электронов и дырок равны n_e=n_p, то приравнивая выражения (16) и (17) получим положение уровня Ферми в запрещенной зоне в зависимости от абсолютной температуры

. (18)

Первые два слагаемых определяют, очевидно, середину запрещенной зоны. Третье слагаемое равно нулю при равенстве эффективных масс электронов и дырок m_e=m_p. Обычно эффективная масса дырки несколько превышает эффективную массу электрона, что дает слабо возрастающую, логарифмическую зависимость от температуры уровня Ферми E_f (T).