Глава 7. Полупроводники

В соответствии с представлениями зонной теории к полупроводникам относятся кристаллы с шириной запрещенной зоны меньшей энергии светового фотона, то есть ΔE<(2-3) эВ. К ним относится широкий класс материалов, электропроводность которых занимает промежуточное положение между электропроводностью металлов ~10⁶-10⁴ Ом ^-1см ^-1 и диэлектриков ~10^-10–10^-12 Ом ^-1см ^-1 (электропроводность указана при комнатной температуре). Характерной особенностью полупроводников является возрастание электропроводности с ростом температуры по экспоненциальному закону

, (1)

что приводит к отрицательному значению температурного коэффициента сопротивления полупроводника . Из формулы (1) следует, что при Т=0 свободные носители заряда отсутствуют, и с ростом температуры электроны из связанного состояния переходят в свободное состояние, преодолев энергетический барьер ΔЕ с вероятностью, определяемую множителем Аррениуса . К полупроводникам относятся кристаллы с ковалентной и ионно-ковалентной связью: Si (кремний), Ge (германий), соединения A₂B₆, A₃B₅ и др.

7.1. Носители заряда в полупроводниках

7.1.1. Законы дисперсии электронов и дырок

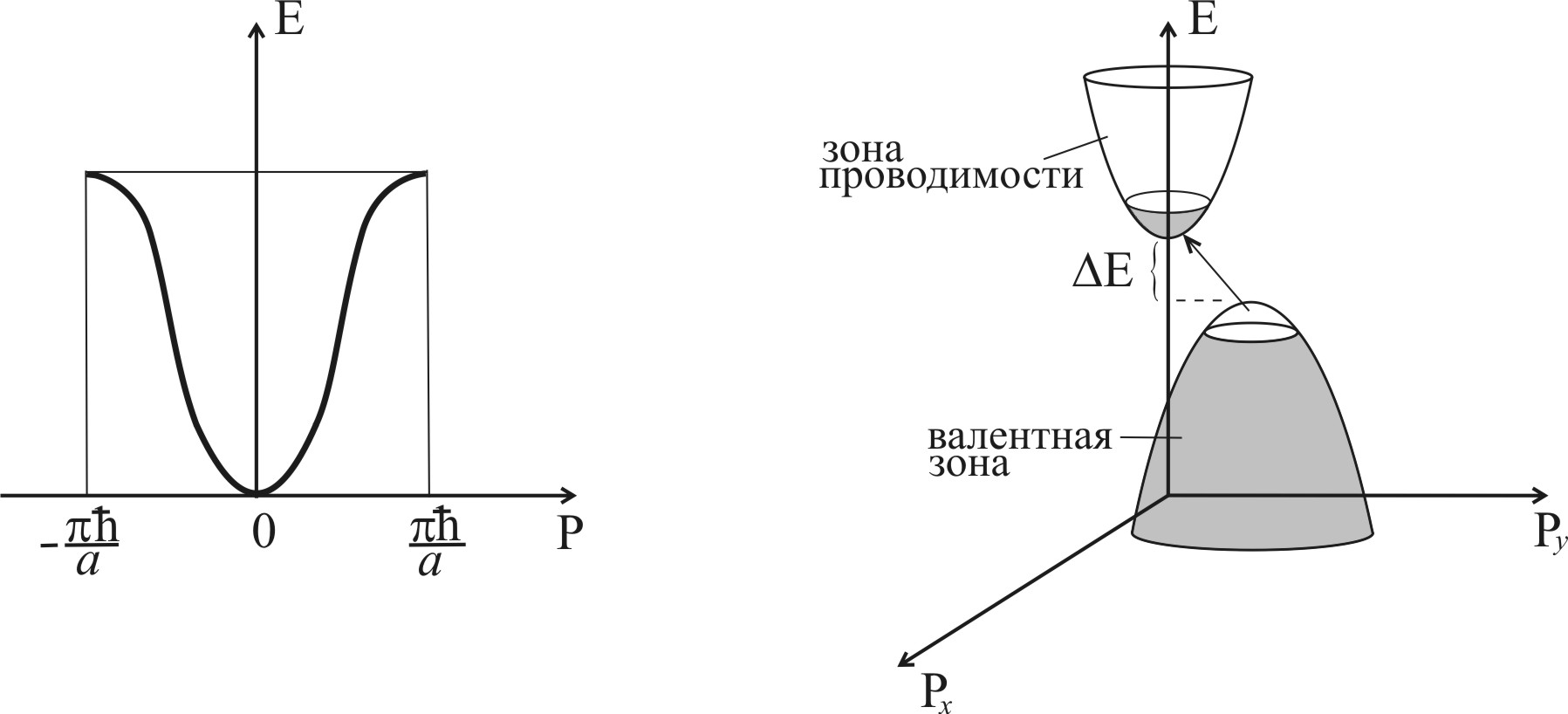
При термическом или фотовозбуждении в полупроводнике образуются электроны в зоне проводимости и дырки в валентной зоне. Закон дисперсии зонного электрона, как следует из зонной теории, имеет точку экстремума (минимум) в центре 1-ой зоны Бриллюэна и максимумы на границах зоны. В этих точках групповая скорость электрона равна нулю.

Так как в проводимости и других явлениях переноса участвуют электроны и дырки, которые находятся вблизи экстремумов функции E(P) в своих зонах, то для получения явного вида закона дисперсии достаточно разложить в ряд Тейлора функцию E(P) вблизи соответствующих минимумов и максимумов.

(а) (б)

Рис. 7.1. Закон дисперсии зонного электрона (а) и схема расположения зоны проводимости и валентной зоны в k-пространстве двумерного кристалла (б)

Для электронов на дне в зоны проводимости получим разложение вблизи минимума:

, (2)

где уровень E_c соответствует дну зоны проводимости. Отсчитывая энергию электрона от дна зоны проводимости и учитывая, что в экстремуме , получим

, (3)

где – эффективная масса электрона проводимости.

Для электронов вблизи потолка валентной зоны имеем:

, (4)

где E_V – потолок валентной зоны, P_г – квазиимпульс электрона на границе зоны Бриллюэна, а – эффективная масса электрона вблизи потолка зоны проводимости. Вблизи максимума функции E(P) вторая производная отрицательна, поэтому эффективная масса электрона вблизи потолка зоны всегда отрицательна, .

Из электродинамики известно, что динамика заряда в электрическом и магнитном полях определяется отношением заряда к массе q/m. Поэтому движение электрона (отрицательного заряда –e) с отрицательной эффективной массой во внешнем электромагнитном поле физически эквивалентно движению некоторой квазичастицы с зарядом +e и положительной эффективной массой . Такая квазичастица называется дыркой.

Для закона дисперсии дырки соответственно имеем согласно (4):

, (5)

где – энергия дырки, отсчитанная от потолка валентной зоны.

Таким образом, носителями заряда в полупроводнике являются электроны вблизи дна зоны проводимости и дырки (положительно заряженные квазичастицы) вблизи потолка валентной зоны с квадратичными законами дисперсии (3) и (5).