- •Содержание
- •Введение
- •Глава 1. Трансляционная симметрия кристалла
- •Глава 2. Колебания атомов кристаллической решётки
- •2.1. Гармоническое приближение
- •2.2. Колебания атомов одномерного кристалла с одним атомом в элементарной ячейке
- •2.3. Колебания одномерного кристалла с двумя атомами в элементарной ячейке
- •2.4. Колебания атомов в трехмерном кристалле
- •Глава 3. Квантовая теория тЕплоёмкосТи кристалла
- •3.1. Модель Дебая
- •3.2. Плотность состояний фононного спектра
- •3.3. Циклические граничные условия Борна-Кармана
- •3.4. Интерполяционная формула Дебая
- •3.5. Законы Дебая и Дюлонга-Пти
- •3.6. Физический смысл температуры Дебая
- •Глава 4. ЭлЕктронные состояния в кристалле
- •4.1.Теорема Блоха
- •4.2. Понятие квазиимпульса
- •4.3. Обратная решётка
- •4.4. Неоднозначность квазиимпульса
- •4.5. Приведение к первой зоне Бриллюэна
- •4.6. Количество состояний в зоне Бриллюэна
- •Глава 5. Элементы зонной теории кристаллов
- •5.1. Метод сильносвязанных электронов
- •5.1.1 Метод сильной связи без учёта симметрии кристалла
- •5.1.2. Метод сильной связи с учётом симметрии кристалла
- •5.2. Метод слабосвязанных электронов
- •5.3. Классификация кристаллов на диэлектрики, полупроводники и металлы
- •Глава 6. Электронная теория металлов
- •6.1. Основные недостатки классической теории металлов.
- •6.2. Уровень Ферми. Поверхность Ферми
- •6.3. Температура Ферми. Критерий вырождения ферми-газа
- •6.4. Электронная теплоёмкость металла
- •6.5. Электрон-фононное взаимодействие и электропроводность металлов
- •6.5.1. Квазиклассические уравнения движения электрона в кристалле.
- •6.5.2. Физический смысл длины свободного пробега электрона
- •6.5.3. Электропроводность нормальных металлов при высоких
- •6.6. Сверхпроводимость
- •Глава 7. Полупроводники
- •7.1. Носители заряда в полупроводниках
- •7.1.1. Законы дисперсии электронов и дырок
- •7.1.2. Статистика носителей заряда в полупроводниках
- •7.1.3. Равновесная концентрация электронов и дырок
- •7.2. Проводимость собственных полупроводников
- •7.3. Проводимость легированных полупроводников
- •7.3.1. Элементарная теория мелких центров
- •7.3.2. Электропроводность легированных полупроводников
- •Глава 8. Методы исследования электронной структуры металлов и полупроводников
- •8.1. Гальваномагнитные методы и циклотронный резонанс
- •8.1.1. Эффект Холла
- •8.1.2. Движение электрона в магнитном поле
- •8.1.3. Циклотронный резонанс в металлах
- •8.2. Квантование энергии электрона в магнитном поле. Уровни Ландау
- •8.3. Квантовые осцилляционные эффекты
- •Литература
- •392008, Г. Тамбов, ул. Советская, 190г
6.5.2. Физический смысл длины свободного пробега электрона
Запишем квазиклассическое уравнение движения электрона в форме (4)
.
Вырожденное
состояние электронов в металле означает,
что за физические свойства металла
ответственны фермиевские электроны,
т.е. электроны, находящиеся вблизи
поверхности Ферми. Поэтому под действием
апериодического потенциала может
измениться лишь направление вектора
,
а его величина
![]() ,
равная радиусу сферы Ферми в
P-пространстве,
остается практически неизменной.
,
равная радиусу сферы Ферми в
P-пространстве,
остается практически неизменной.
Если при взаимодействии
электрона с деформационным потенциалом
дефекта или упругой волны (фононом)
направление распространения электрона
меняется на угол около
![]() ,
то такое взаимодействие “выбивает”
электрон из потока в направлении,
задаваемым внешним электрическим полем.
Это означает, что металлический кристалл
с дефектом и/или фононами оказывает
сопротивление движению электронов.
Такое взаимодействие электронов металла
с несовершенствами кристаллического
порядка называется рассеянием.
Поэтому длина
свободного пробега электрона
определяется как расстояние между
последовательными актами рассеяния
электрона.
,
то такое взаимодействие “выбивает”
электрон из потока в направлении,
задаваемым внешним электрическим полем.
Это означает, что металлический кристалл
с дефектом и/или фононами оказывает
сопротивление движению электронов.
Такое взаимодействие электронов металла
с несовершенствами кристаллического
порядка называется рассеянием.
Поэтому длина
свободного пробега электрона
определяется как расстояние между
последовательными актами рассеяния
электрона.
Таким образом,
физической причиной электрического
сопротивления металла является рассеяние
фермиевских электронов на дефектах
решетки, фононах и деформационном
потенциале, связанным с действием
внешних сил, что объясняет эмпирическое
правило Матиссена:
![]() ,
так как все три слагаемых отражают связь
сопротивления металла с нарушением
симметрии кристалла различной природы
– структурные дефекты, фононы и внешние
силы.
,
так как все три слагаемых отражают связь
сопротивления металла с нарушением
симметрии кристалла различной природы
– структурные дефекты, фононы и внешние
силы.
6.5.3. Электропроводность нормальных металлов при высоких
и низких температурах
Электроны
проводимости имеют энергию, близкую к
энергии Ферми
![]() эВ
и длину волны
эВ
и длину волны
![]() нм, соизмеримую с межатомным расстоянием
нм, соизмеримую с межатомным расстоянием
![]() нм.
Внешнее электрическое поле изменяется
на расстоянии значительно превышающем
параметр решетки. Поэтому по отношению
к кристаллическому потенциальному полю
фермиевский электрон является квантовым
объектом, а по отношению к внешнему полю
– квазиклассическим. Его поведение во
внешнем поле описывается с помощью
квазиклассических уравнений движения
(4) и (5), в которых импульс заменен на
квазиимпульс, результирующая сила –
на внешнюю силу, а масса – на эффективную
массу
,
определяемую законом дисперсии
.
нм.
Внешнее электрическое поле изменяется
на расстоянии значительно превышающем
параметр решетки. Поэтому по отношению
к кристаллическому потенциальному полю
фермиевский электрон является квантовым
объектом, а по отношению к внешнему полю
– квазиклассическим. Его поведение во
внешнем поле описывается с помощью
квазиклассических уравнений движения
(4) и (5), в которых импульс заменен на
квазиимпульс, результирующая сила –
на внешнюю силу, а масса – на эффективную
массу
,
определяемую законом дисперсии
.
Функция
имеет чисто квантовую природу и
рассчитывается путём решения одночастичного
уравнения Шрёдингера для зонного
электрона (см. методы сильной и слабой
связи). При этом многие формулы
классической физики применимы к описанию
зонного электрон во внешних полях с
учетом соответствующих замен. Поэтому
для расчета электропроводности металла
![]() может быть использована формула
Друде-Лоренца с заменой массы электрона
на эффективную массу, т.е.
может быть использована формула
Друде-Лоренца с заменой массы электрона
на эффективную массу, т.е.
![]() , (5)
, (5)
где
![]() – концентрация электронов, – элементарный
заряд,
– концентрация электронов, – элементарный
заряд,
![]() – время релаксации. Умножим числитель
и знаменатель этой формулы на фермиевскую
скорость электрона, определяемую уровнем
Ферми
– время релаксации. Умножим числитель
и знаменатель этой формулы на фермиевскую
скорость электрона, определяемую уровнем
Ферми
![]() ,
получим
,
получим
![]() , (6)
, (6)
где
![]() – фермиевский импульс, т.е. радиус сферы
Ферми, а
– фермиевский импульс, т.е. радиус сферы
Ферми, а
![]() – длина свободного пробега электрона.
Так как электроны в металле образуют
вырожденный ферми-газ, то в электропроводности
участвуют лишь электроны, находящиеся
вблизи уровня Ферми, т.е. имеющие
фермиевский импульс , величина которого
практически не зависит от температуры.
Поэтому температурная зависимость
электропроводности металла будет
определяться, в основном, температурной
зависимостью длины свободного пробега
– длина свободного пробега электрона.
Так как электроны в металле образуют
вырожденный ферми-газ, то в электропроводности
участвуют лишь электроны, находящиеся
вблизи уровня Ферми, т.е. имеющие
фермиевский импульс , величина которого
практически не зависит от температуры.
Поэтому температурная зависимость
электропроводности металла будет
определяться, в основном, температурной
зависимостью длины свободного пробега
![]() ,
т.е. расстоянием между последовательными
актами рассеяния электрона на фононах.
Поскольку в результате рассеяния
направление вектора импульса электрона
должно изменяться на угол около
,
то импульс фонона должен иметь значение,
близкое к фермиевскому импульсу (рис.
6.5.).
,
т.е. расстоянием между последовательными
актами рассеяния электрона на фононах.
Поскольку в результате рассеяния
направление вектора импульса электрона
должно изменяться на угол около
,
то импульс фонона должен иметь значение,
близкое к фермиевскому импульсу (рис.
6.5.).
|
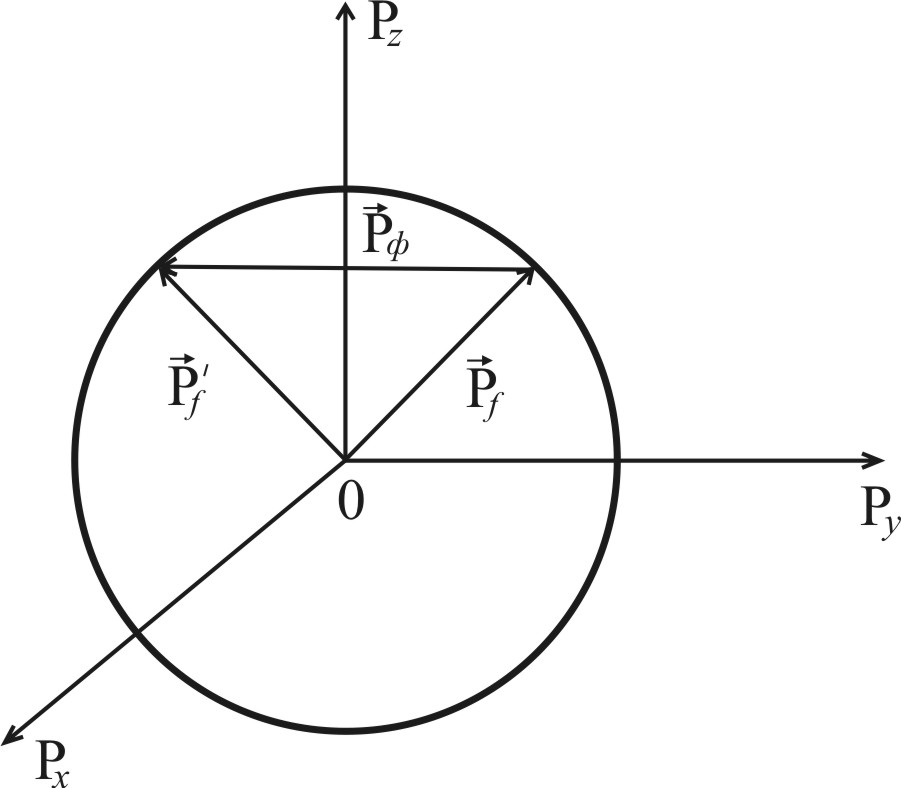
Рис. 6.5. Изменение вектора импульса фермиевского электрона при рассеянии на фононе |
Поэтому общее условие рассеяния электрона на фононе можно записать в виде
![]() . (7)
. (7)
В модели металла,
в которой электроны рассматриваются
как идеальный ферми-газ, длина свободного
пробега обратно пропорциональна числу
актов рассеяния
![]() ,
т.е.
,
т.е.
![]() . (8)
. (8)
Рассмотрим характер электрон-фононного взаимодействия при различных температурах и его связь с температурной зависимостью электрического сопротивления металла.
Высокие температуры
В области высоких
температур, т.е. при температурах выше
дебаевской температуры,
![]() ,
нагревание кристалла происходит, в
основном, за счет возбуждения дебаевских
фононов, имеющих одинаковую энергию
,
нагревание кристалла происходит, в
основном, за счет возбуждения дебаевских
фононов, имеющих одинаковую энергию
![]() .
Поэтому тепловая энергия кристалла
будет складываться из энергии дебаевских
фононов
.
Поэтому тепловая энергия кристалла
будет складываться из энергии дебаевских
фононов
![]() .
С другой стороны, в области высоких
температур теплоёмкость кристалла
подчиняется закону Дюлонга-Пти
,
а тепловая энергия является линейной
функцией температуры
.
С другой стороны, в области высоких
температур теплоёмкость кристалла
подчиняется закону Дюлонга-Пти
,
а тепловая энергия является линейной
функцией температуры
![]() .
Отсюда видно, что при , число фононов
пропорционально первой степени
температуры
.
Отсюда видно, что при , число фононов
пропорционально первой степени
температуры
![]() .
.
Оценим эффективность электрон-фононного взаимодействия в этой области температур. Импульс фонона оценим из закона дисперсии акустических фононов
![]() . (9)
. (9)
|
Рис. 6.6. Закон дисперсии акустических фононов
|
Предельная частота
![]() соответствует границе зоны Бриллюэна
соответствует границе зоны Бриллюэна
![]() (рис. 6.6.). Следовательно, импульс
дебаевского фонона равен
(рис. 6.6.). Следовательно, импульс
дебаевского фонона равен
![]() .
.
Для вычисления
фермиевского импульса
![]() ,
т.е. радиуса сферы Ферми, отделяющей в
,
т.е. радиуса сферы Ферми, отделяющей в
![]() -пространстве
область заполненных состояний от
незаполненных электронных состояний,
оценим сначала число заполненных
состояний
-пространстве
область заполненных состояний от
незаполненных электронных состояний,
оценим сначала число заполненных
состояний
![]() .
.
Здесь в числителе
– объём, ограниченный сферой Ферми,
т.е.
![]() ,
а в знаменателе – объём -пространства,
приходящийся на одно квантовое состояние
,
а в знаменателе – объём -пространства,
приходящийся на одно квантовое состояние
![]() .
Следовательно,
.
Следовательно,
![]() .
Учитывая, что по принципу Паули в каждом
квантом состоянии можно разместить по
два электрона с противоположными
спинами, получим для концентрации
электронов
.
Учитывая, что по принципу Паули в каждом
квантом состоянии можно разместить по
два электрона с противоположными
спинами, получим для концентрации
электронов
![]()
![]() ,
откуда
,
откуда
![]() . (10)
. (10)
Для одновалентного
металла с простой кубической решеткой
![]() и
и
![]() .
Таким образом, значение импульса
фермиевского электрона приблизительно
равно величине импульса дебаевского
фонона и, следовательно, условие рассеяния
(7) соблюдается в каждом акте
электрон-фононного взаимодействия.
Поэтому число актов рассеяния будет
равно числу дебаевских фононов
.
Таким образом, значение импульса
фермиевского электрона приблизительно
равно величине импульса дебаевского
фонона и, следовательно, условие рассеяния
(7) соблюдается в каждом акте
электрон-фононного взаимодействия.
Поэтому число актов рассеяния будет
равно числу дебаевских фононов
![]() .
Так как число фононов линейно растет с
температурой при , то учитывая (8) и (6)
получим, что электропроводность металла
при высоких температурах
~
.
Так как число фононов линейно растет с
температурой при , то учитывая (8) и (6)
получим, что электропроводность металла
при высоких температурах
~![]() ,
а удельное сопротивление
соответственно растет пропорционально
температуре
,
а удельное сопротивление
соответственно растет пропорционально
температуре
![]() ,
при . (11)
,
при . (11)
Эту линейную связь обычно записывают в следующем виде
![]() ,
,
где
![]() – температурный коэффициент сопротивления
металла.
– температурный коэффициент сопротивления
металла.
Низкие температуры
Рассмотрим область
низких температур, т.е. значительно
меньших, чем характеристическая
температура Дебая,
![]() .
Нагревание в области криогенных
температур носит квантовый характер.
С ростом температуры фононы, которые
являются бозонами, возбуждаются по
одиночке, заполняя последовательно
самые низкие частоты в спектре. В области
низких частот закон дисперсии линеен
.
Нагревание в области криогенных
температур носит квантовый характер.
С ростом температуры фононы, которые
являются бозонами, возбуждаются по
одиночке, заполняя последовательно
самые низкие частоты в спектре. В области
низких частот закон дисперсии линеен
![]() .
Волновые числа таких фононов находятся
вблизи центра зоны Бриллюэна, что
соответствует длинноволновой области
спектра
.
Волновые числа таких фононов находятся
вблизи центра зоны Бриллюэна, что
соответствует длинноволновой области
спектра
![]() .
.
Импульсы
длинноволновых фононов значительно
меньше граничного импульса
![]() ,
соответствующего минимальной длине
волны фонона
,
соответствующего минимальной длине
волны фонона
![]() .
Так как импульс фермиевского электрона,
как было показано, приблизительно равен
импульсу фонона на границе зоны Бриллюэна
.
Так как импульс фермиевского электрона,
как было показано, приблизительно равен
импульсу фонона на границе зоны Бриллюэна
![]() ,
то получаем, что в области низких
температур импульс фонона значительно
меньше импульса электрона
,
то получаем, что в области низких
температур импульс фонона значительно
меньше импульса электрона
![]() ,
и один акт электрон-фононного взаимодействия
не приведет к рассеянию.
,
и один акт электрон-фононного взаимодействия
не приведет к рассеянию.
Оценим количество
взаимодействий, необходимых для рассеяния
электрона при
![]() .
Пусть вследствие взаимодействия с
фононом импульс электрона
.
Пусть вследствие взаимодействия с
фононом импульс электрона
![]() поворачивается на небольшой угол
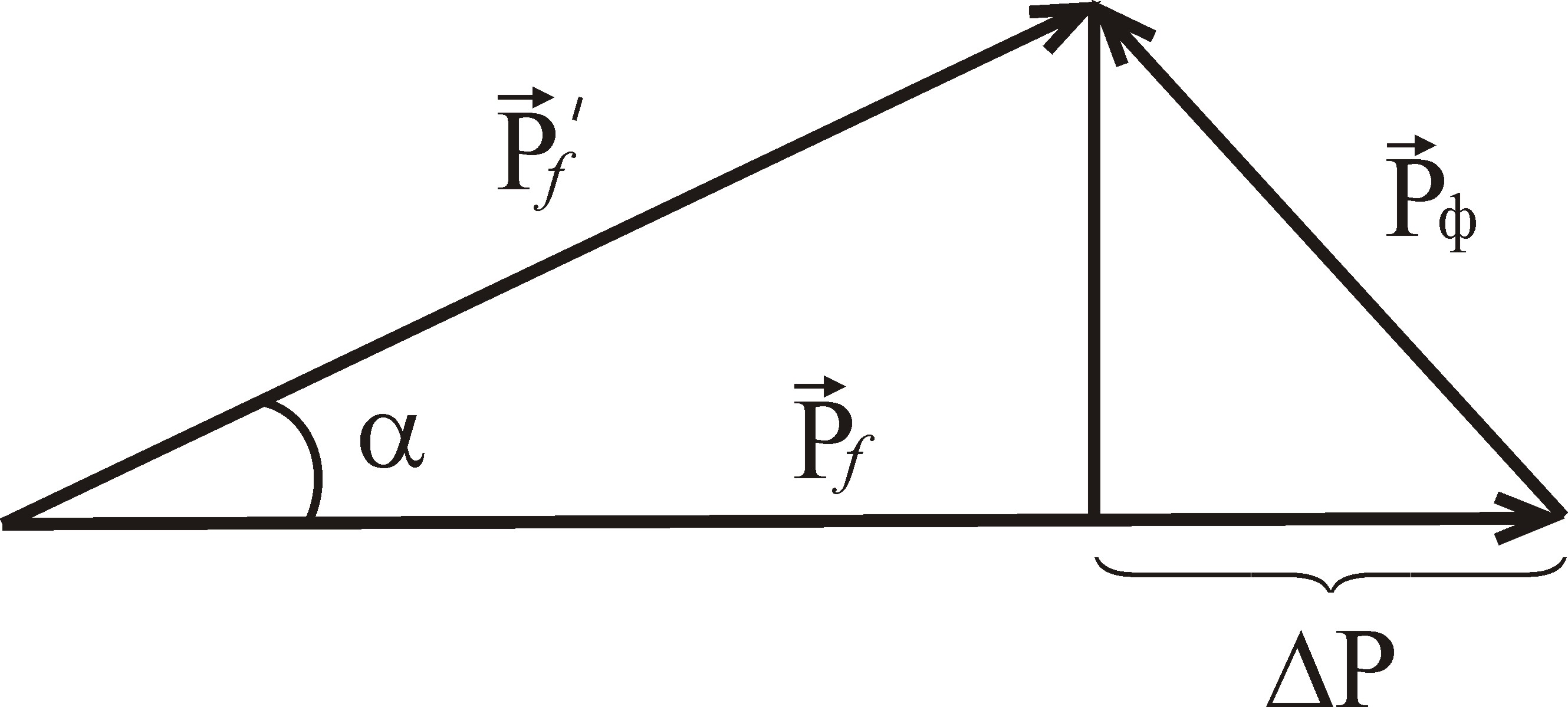
и становится равным (рис. 6.7).
поворачивается на небольшой угол
и становится равным (рис. 6.7).
|
Рис. 6.7. Схема взаимодействия фермиевского электрона с длинноволновым фононом |
В результате такого
взаимодействия электрон остается вблизи
поверхности (сферы) Ферми, поэтому
![]() ,
но его вклад в электропроводность
уменьшается, так как проекция вектора
,
но его вклад в электропроводность
уменьшается, так как проекция вектора
![]() на первоначальное направление
становится меньше на величину
на первоначальное направление
становится меньше на величину
![]() :
:
![]() .
.![]()
При малых значениях
аргумента
![]() ,
поэтому
,
поэтому
![]() .
.
Так как импульс
фермиевского электрона приблизительно
равен импульсу фонона на границе зоны
Бриллюэна
![]() ,
а отношение импульса фермиевского
фонона к граничному, с учетом закона
дисперсии:
,
а отношение импульса фермиевского
фонона к граничному, с учетом закона
дисперсии:
![]() ,
,
то температурная зависимость эффективности электрон-фононного взаимодействия будет пропорциональна квадрату температуры:
![]() . (12)
. (12)
Величина, обратная
эффективности отдельного взаимодействия
фонона с электроном, приблизительно
характеризует число электрон-фононных
взаимодействий, приводящих к одному
акту рассеяния фермиевского электрона.
Типичное значение температуры Дебая
![]() К,
поэтому в области гелиевых температур
К,
поэтому в области гелиевых температур
![]() и рассеяние электрона носит непрерывный
характер.
и рассеяние электрона носит непрерывный
характер.
Рассмотрим теперь
температурную зависимость числа фононов
![]() при низких температурах. Число квантовых
фононных состояний оценим как отношение
объёма
-пространства,
занятого системой, к объёму, приходящемуся
на одно квантовое состояние. Так как
фононы являются бозонами, то число
фононов равно числу занятых квантовых
состояний
при низких температурах. Число квантовых
фононных состояний оценим как отношение
объёма
-пространства,
занятого системой, к объёму, приходящемуся
на одно квантовое состояние. Так как
фононы являются бозонами, то число
фононов равно числу занятых квантовых
состояний
![]() .
.
Учитывая линейный
закон дисперсии в этой области температур
![]() ,
получим,
что число фононов пропорционально
третьей степени температуры, т.е.
,
получим,
что число фононов пропорционально
третьей степени температуры, т.е.
![]() . (13)
. (13)
Количество актов рассеяния определим как произведение числа фононов на эффективность электрон-фононного взаимодействия
![]() . (14)
. (14)
Подставляя сюда температурные зависимости (12) и (13), имеем
![]() . (15)
. (15)
Таким образом,
температурная зависимость количества
актов рассеяния, а следовательно и
удельного сопротивления металла
определяется законом
![]() в области криогенных температур:
в области криогенных температур:
![]() . (16)
. (16)
Эта зависимость называется законом Блоха.
|
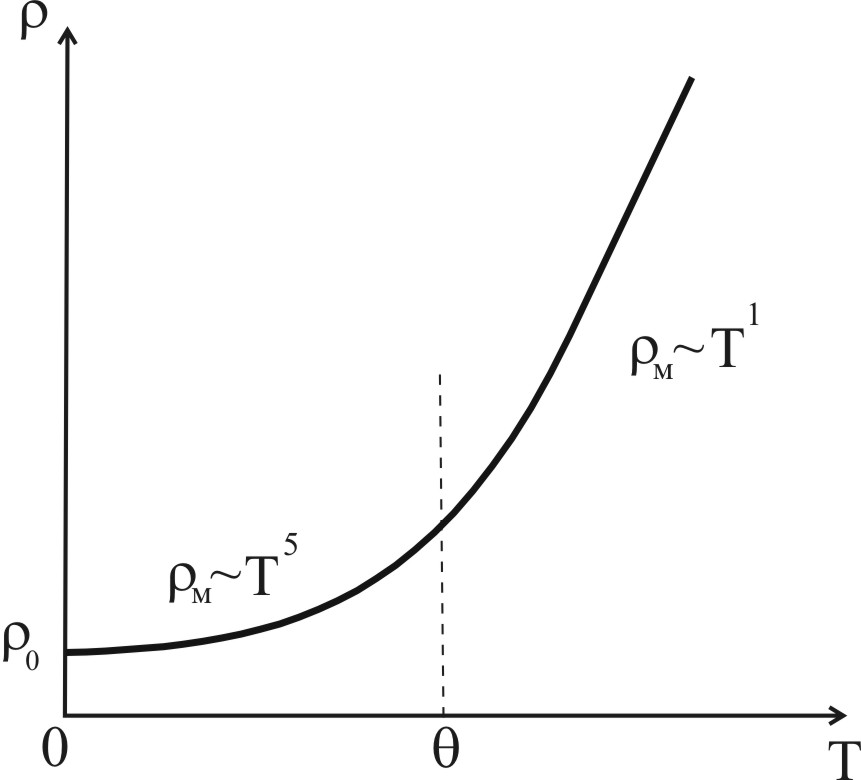
Рис.6.8. Температурная зависимость
удельного сопротивления нормального
металла.
|
Сопротивление идеальной решетки (без дефектов) при любом значении температуры было вычислено Блохом и Грюнайзеном в рамках идеализированной модели, основанной на следующих предположениях:
1) рассматривается идеальный Ферми-газ электронов в решетке,
2) для описания тепловых колебаний использовалась дебаевская модель фононного спектра.
При таких предположениях для сопротивления металла были получены следующие формулы:
![]() , (17)
, (17)
где – атомный вес
металла,
![]() – постоянная, связанная с удельным
объёмом. В области низких и высоких
температур формула (17) переходит в
следующие выражения:
– постоянная, связанная с удельным
объёмом. В области низких и высоких
температур формула (17) переходит в
следующие выражения:
![]() при
при
![]() ,
,
![]() при
при
![]() . (18)
. (18)
Эти формулы дают возможность измерения дебаевской температуры по измерению электрического сопротивления металла при разных температурах.
На рис. 6.8. показана
температурная зависимость удельного
сопротивления
![]() нормального металла в области температур
от криогенных до предплавильных. При
высоких температурах T>
она хорошо описывается линейным законом,
а в области криогенных температур
нормального металла в области температур
от криогенных до предплавильных. При
высоких температурах T>
она хорошо описывается линейным законом,
а в области криогенных температур
![]() <<
законом Блоха
~
<<
законом Блоха
~![]() и стремится к остаточному значению
и стремится к остаточному значению
![]() ,
которое определяется концентрацией
дефектов кристаллической решетки
металла.
,
которое определяется концентрацией
дефектов кристаллической решетки
металла.