6.5. Электрон-фононное взаимодействие и электропроводность металлов
Из зонной теории
следует, что состояние зонного электрона
в идеальном кристалле определяется
законом дисперсии
,
т.е. зависимостью энергии электрона от
квазиволнового вектора (или квазиимпульса
), а его скорость есть групповая скорость
блоховских волн
.
Таким образом, интегралами движения
зонного электрона является его полная
энергия
,
квазиимпульс
,
групповая скорость
,
а следовательно и ускорение
,
равное нулю, что соответствует бесконечной
длине свободного пробега. Можно сказать,
что идеальная кристаллическая решетка
не оказывает сопротивления движению
электрона. Этот результат является
следствием интерференции блоховских
волн на кристаллической решетке, т.е.
непосредственно связан с трансляционной
симметрией кристалла.
6.5.1. Квазиклассические уравнения движения электрона в кристалле.
Эффективная масса электрона
Рассмотрим движение
зонного электрона при наличии
апериодической составляющей потенциального
рельефа
,
которая может быть связана с деформационным
потенциалом дефекта решетки, например,
примесного атома или с внешним полем
(упругим или электромагнитным). Оператор
Гамильтона электрона в таком кристалле
будет суммой гамильтониана идеального
кристалла
и апериодической добавки , т.е.
.
Потенциал
нарушает трансляционную симметрию
кристалла, поэтому квазиимпульс уже не
будет интегралом движения. Изменение
квазиимпульса во времени можно рассчитать
с помощью анализа уравнения движения
в форме Гейзенберга
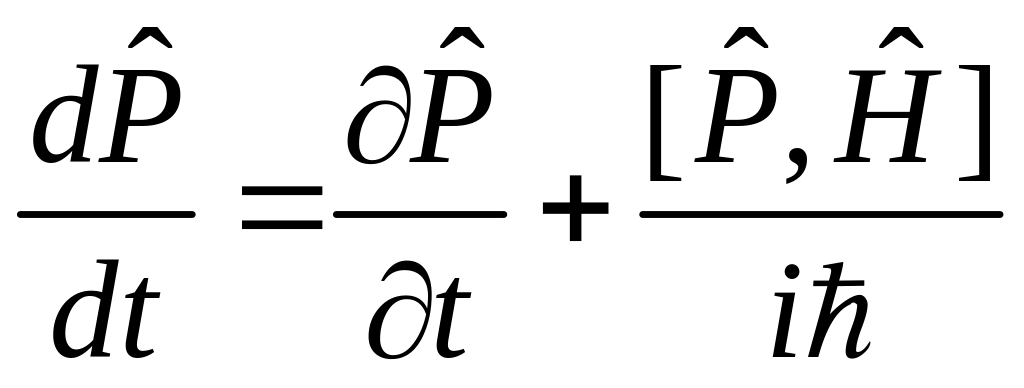, (1)
где
– оператор квазиимпульса. Так как
не зависит явно от времени, то
.
В идеальной кристаллической решетке
квазиимпульс электрона и его полная
энергия сохраняются. Поэтому оператор
квазиимпульса коммутирует с , т.е.
и квантовое уравнение движения (1) примет
вид:
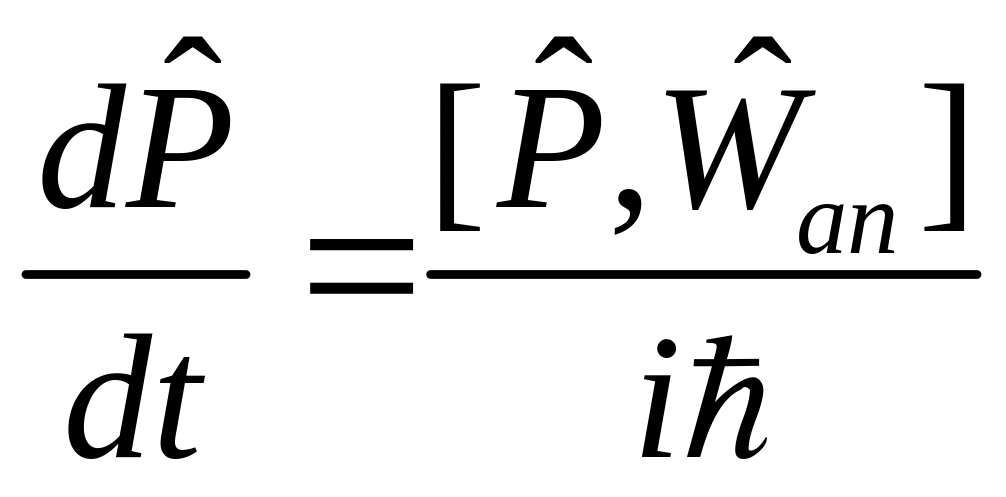. (2)
Запишем оператор
квазиимпульса в виде:
,
где
– оператор умножения, тогда
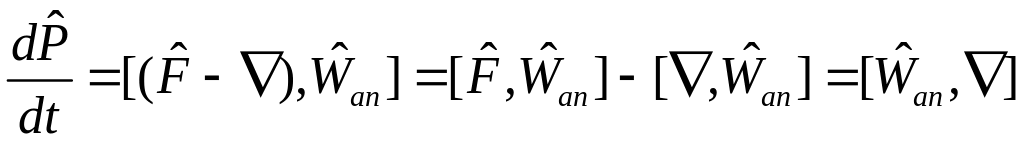. (3)
Здесь
,
так как оба оператора и
являются операторами умножения. Вычислим
оператор
:
.
Подставляя полученный результат в (2) и используя «формулу среднего», перейдем от операторов к квантовомеханическим средним величинам:
. (4)
Левая часть (4)
имеет размерность силы и называется
“внешней” силой
,
так как её действие на электрон связано
с апериодической составляющей
потенциального рельефа, нарушающую
трансляционную симметрию идеального
кристалла.
Таким образом, несохранение квазиимпульса обусловлено нарушением трансляционной симметрии кристалла вызванное, например, наличием структурных дефектов, фононов и действием внешних механических сил или воздействием внешнего электромагнитного поля. Уравнение (4) ещё записывают в виде
. (
)
Это уравнение по
форме аналогично классическому уравнению
динамики, в котором импульс заменен на
квазиимпульс
,
а результирующая сила – на внешнюю силу
.
Поскольку
квазиимпульс под действием внешней
силы уже не сохраняется, то и групповая
скорость электрона
также не будет интегралом движения.
Кинематическое ускорение электрона
формально можно выразить только через
внешние силы.
Запишем уравнение
(
)
для одномерного случая
:
.
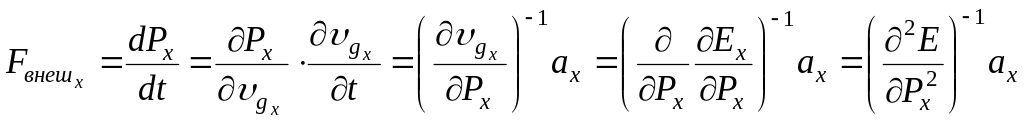Мы видим, что
кинематическое ускорение электрона
вдоль оси
связано с соответствующей проекцией
внешней силы с помощью множителя
,
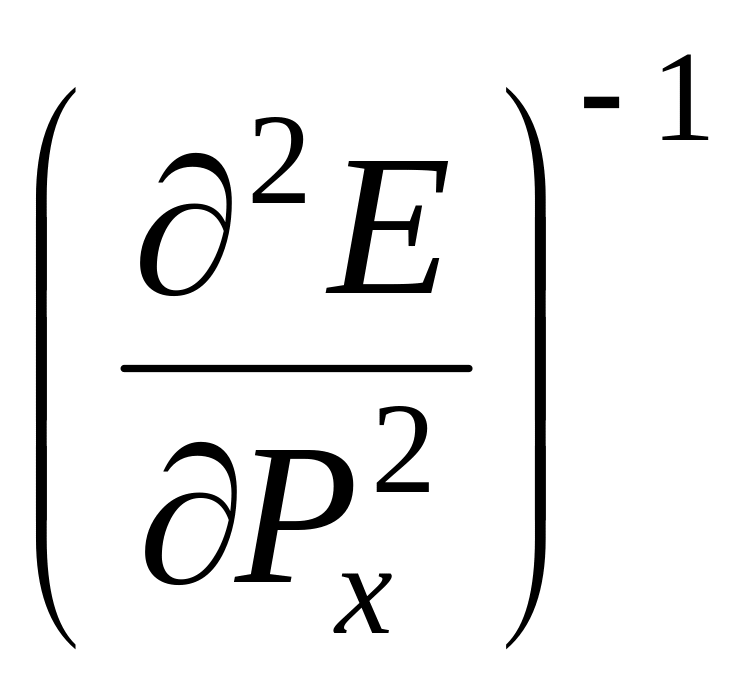называемой эффективной массой электрона
,
т.е.
,
(5)
где
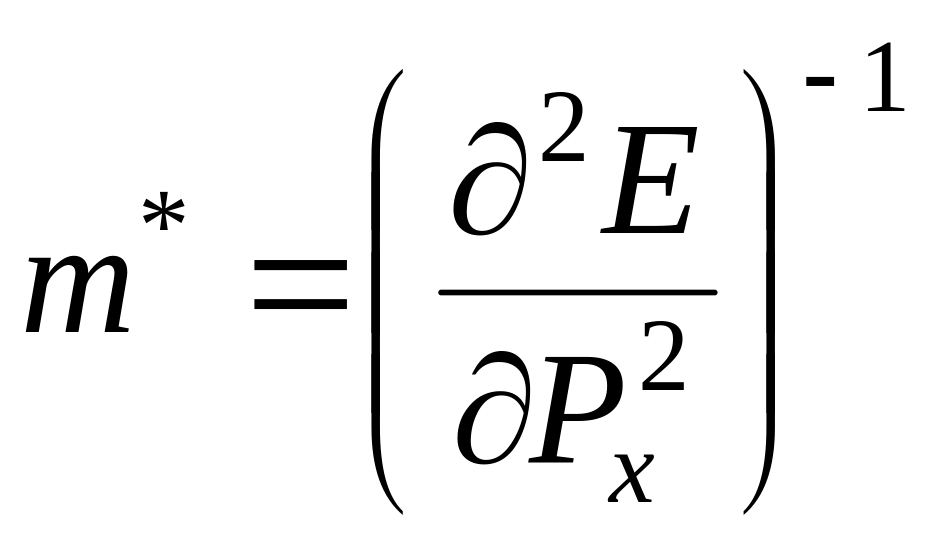– эффективная масса электрона.
В трёхмерном случае
производные закона дисперсии
образуют симметричный тензор второго
ранга, называемый тензором обратных
эффективных масс, и связь между ускорением
и силой будет иметь вид
, (
)
где – компоненты
тензора эффективных масс:
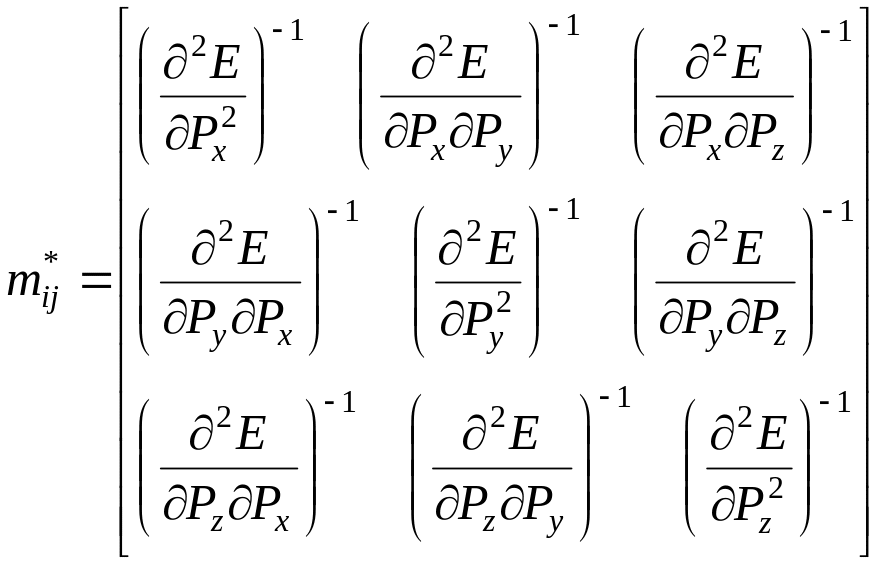
Уравнения (4) и (5) называют квазиклассические уравнения движения электрона в кристалле.
Знание компонент тензора эффективных масс позволяет описывать движение электрона действием только внешних сил. При этом многие формулы, полученные для электрона в свободном пространстве, оказываются применимыми для электрона в решетке при замене массы свободного электрона на соответствующую компоненту тензора эффективных масс.