Глава 6. Электронная теория металлов

6.1. Основные недостатки классической теории металлов.

Первая квантовая теория металлов

Классическая теория металлов Друде-Лоренца (1900г.) объяснила эмпирические законы Ома, Джоуля-Ленца и Видемана-Франца, но не смогла объяснить явление сверхпроводимости, температурную зависимость электропроводности нормальных металлов, почти полное отсутствие электронной теплоёмкости металла и т.д.. Кроме того, в классической теории не находит объяснение эмпирическое правило Матиссена, устанавливающее зависимость удельного сопротивления нормальных металлов от концентрации дефектов кристаллического строения п_d, температуры Т и действия внешних механических сил F_мех, вызывающих упругую деформацию металла

. (1)

Из правила Матиссена в частности следует, что при понижении температуры в области криогенных температур, удельное сопротивление металла стремится не к нулю, а к некоторой остаточной величине , которая является мерой дефектности кристаллического строения металла.

Первая квантовая теория металлов была предложена Зоммерфельдом в 1928г. В отличие от классической теории Друде-Лоренца, рассматривающей электронную подсистему металла как классический идеальный газ, подчиняющийся статистике Максвелла-Больцмана, в теории металлов Зоммерфельда учитывается тот факт, что электроны являются фермионами (частицами с полуцелым спиновым числом) и подчиняются квантовой статистике Ферми-Дирака.

Таким образом, в квантовой теории Зоммерфельда металл рассматривается как ящик с идеальным ферми-газом электронов. Электроны считаются свободными частицами с квадратичным законом дисперсии, т.е. их потенциальная энергия взаимодействия с другими электронами и с ионами решётки предполагается пренебрежимо малой, поэтому полная энергия электрона есть его кинетическая энергия , волновые функции электрона есть собственные функции оператора импульса, т.е. плоские волны де Бройля: , а статистические свойства электронного газа определяются функцией распределения Ферми-Дирака

, (2)

где  вероятность заполнения уровня Е, E_f – уровень Ферми, или граничная энергия, которая при Т=0 отделяет область заполненных уровней от области незаполненных уровней в квазинепрерывном энергетическом спектре электронов металла.

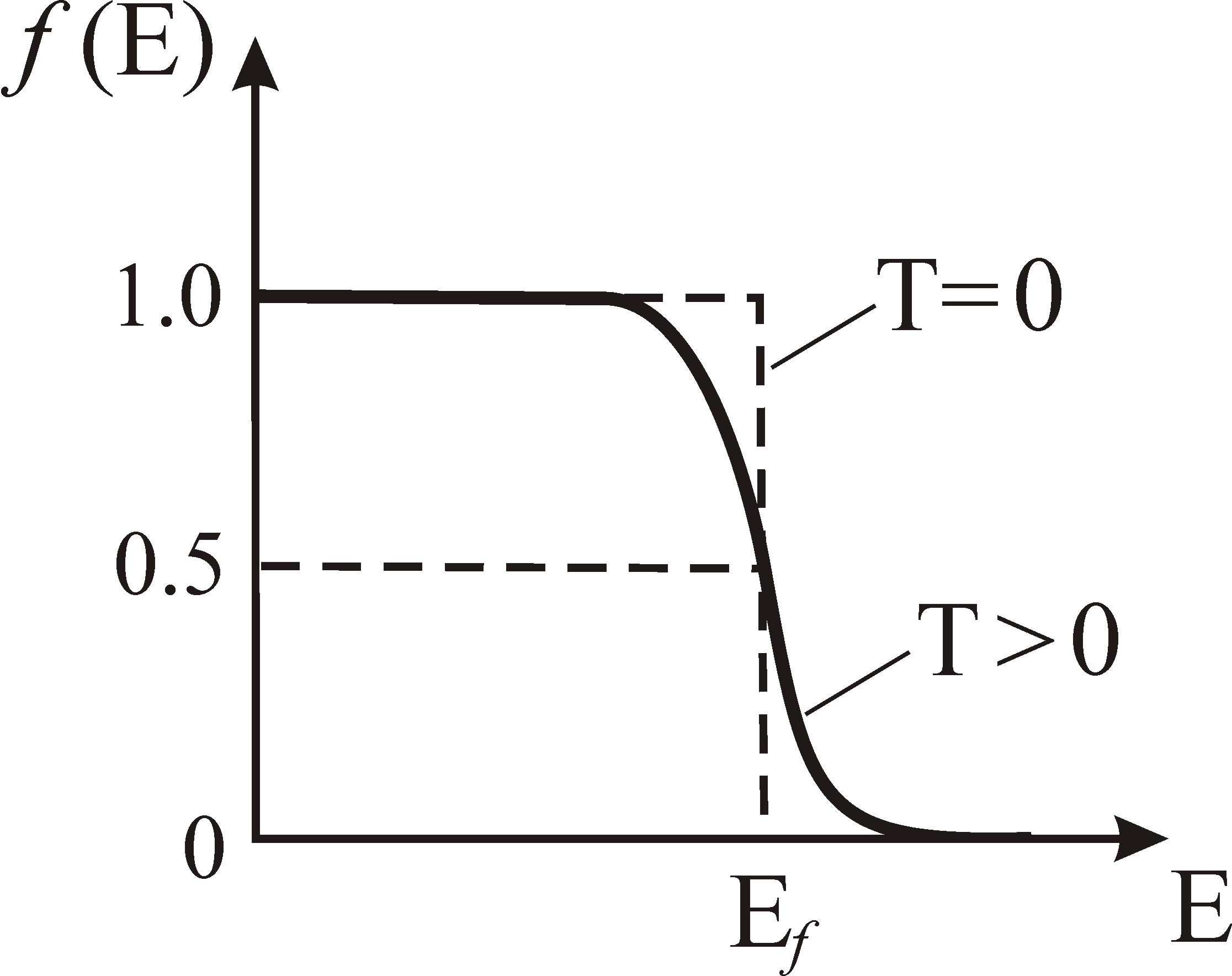
Рис. 6.1. Распределение Ферми-Дирака при температуре Т=0 К («ступенька Ферми») и температуре Т>0 К

При нагревании металла электроны с заполненных уровней под уровнем Ферми переходят на свободные уровни Е>E_f, что приводит к размыванию «ступеньки Ферми». В этом случае граничная энергия Ферми определяется как уровень, вероятность заполнения которого равна 0.5 ( рис. 6.1.).

6.2. Уровень Ферми. Поверхность Ферми

В приближении свободных электронов их закон дисперсии изотропен и квадратичен , поэтому изоэнергетическая поверхность в k-пространстве есть сфера. Изоэнергетическая поверхность, соответствующая уровню Ферми, называется поверхностью Ферми. При абсолютном нуле поверхность Ферми отделяет в k-пространстве область заполненных электронных состояний от незаполненных.

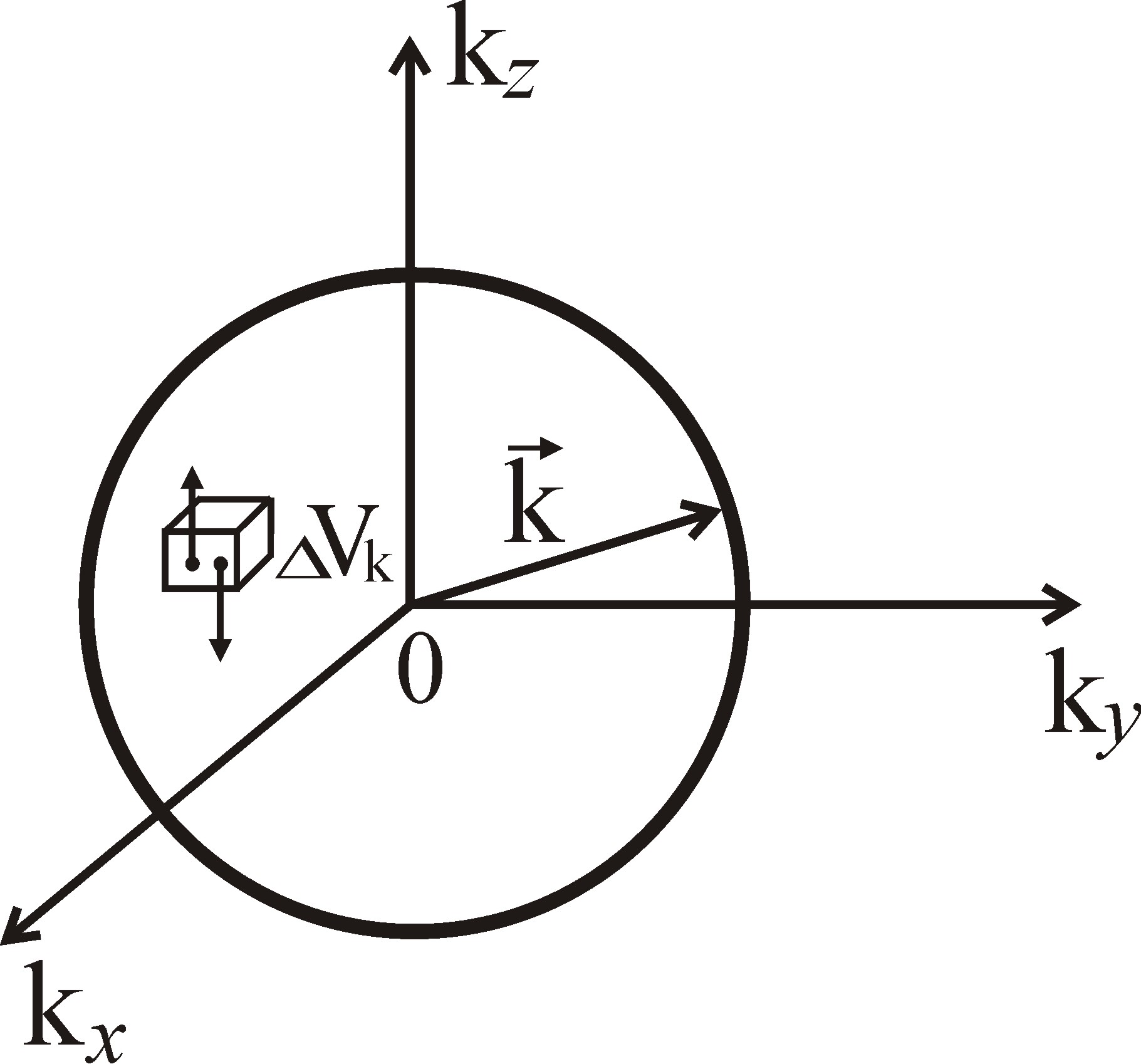
Рис. 6.2 Поверхность Ферми для электронов с изотропным и квадратичным законом дисперсии

Для кристалла конечных размеров k-пространство электронных состояний дискретно. Это непосредственно следует из циклических граничных условий Борна-Кармана:

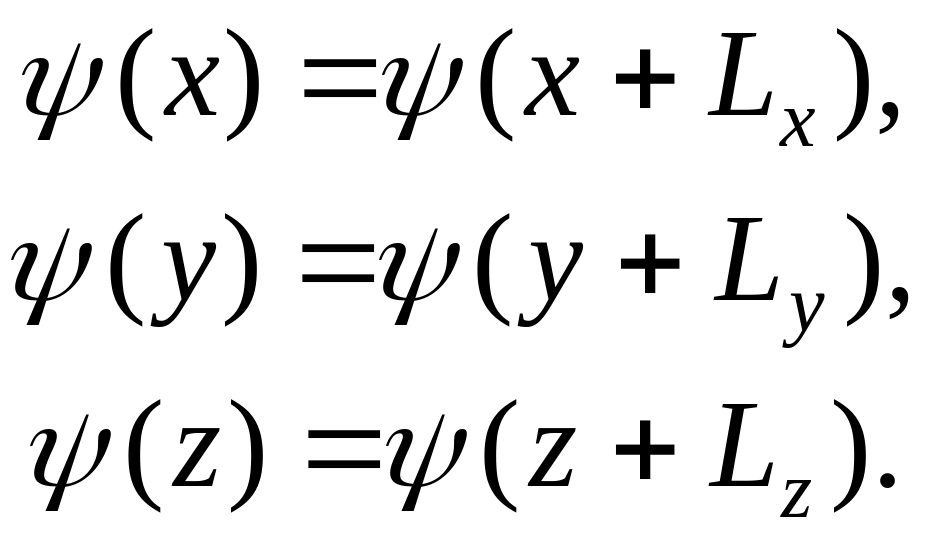
Подставим в первое уравнение волновую функцию электрона

,

получим , откуда , где п – целые числа. Поэтому на одно электронное состояние приходится отрезок , а в трёхмерном случае, очевидно объём:

,

где V=L_xL_yL_z – объём кристалла.

Электронные состояния с энергиями, меньшими энергии Ферми E_f, находятся в k-пространстве в шаре радиусом . Их количество N равно отношению объёма шара, ограниченного поверхностью Ферми, к объёму , приходящемуся на одно квантовое состояние

.

По принципу Паули в каждом заполненном квантовом состоянии находятся два электрона с противоположно направленными спиновыми угловыми моментами, поэтому количество электронов N_эл=2N, а концентрация электронов соответственно равна

.

Для радиуса сферы Ферми и уровня Ферми имеем:

, (3)

. (4)

Таким образом, уровень Ферми полностью определяется концентрацией свободных электронов n. Для одновалентного металла с простой кубической решёткой очевидно , где а – параметр решётки, поэтому . Принимая для оценки а=0.3 нм, получим . Для типичных металлов уровень Ферми . Полезны также оценки скорости и длины волны электронов вблизи уровня Ферми: м/с, нм.

Фермиевская скорость, как видно, значительно превышает скорость звука , что вызывает эффект испускания электроном фонона и специфическое взаимодействие электронов за счёт обмена виртуальными фононами и приводит к переходу в сверхпроводящее состояние при охлаждении ряда металлов в области криогенных температур. Соизмеримость длины волны фермиевского электрона с параметром решётки означает, кроме того, что фермиевский электрон является квантовым объектом в металлическом кристалле.