5.2. Метод слабосвязанных электронов

Если метод сильной связи применяют для расчёта электронной структуры диэлектриков и полупроводников, то в методе слабой связи электроны считаются слабо связанными с атомами, что соответствует случаю металла. В первой квантовой теории металлов, предложенной Зоммерфельдом (1928г), металл рассматривается как ящик с ферми-газом электронов. В методе слабосвязанных электронов модель Зоммерфельда берётся в качестве нулевого приближения теории возмущения, а возмущением является периодический потенциал кристаллической решётки. Из теории возмущения для непрерывного спектра известно, что при наличии периодического возмущения непрерывный спектр разбивается на чередующиеся разрешённые и запрещённые зоны.

Таким образом, в нулевом приближении валентные электроны металла считаются свободными. Оператор Гамильтона свободного электрона есть оператор кинетической энергии , его волновая функция – собственная функция оператора импульса, т.е. плоская волна де Бройля – , а закон дисперсии электрона квадратичен . Роль малого возмущения играет периодический потенциал кристаллической решётки: , где  вектор решётки. Задача сводится к нахождению закона дисперсии электрона с гамильтонианом . Основные результаты расчёта состоят в следующем.

При наличии периодического потенциала решётки k-пространство разбивается на зоны Бриллюэна, на границах которых соблюдается закон Вульфа-Брэгга. В одномерном случае на границах первой зоны Бриллюэна в точках и происходит образование стоящей волны с длиной . Электрон на границе зоны Бриллюэна не переносит заряд, его групповая скорость равна нулю, что соответствует условию брэгговского отражения.

Из волновой физики известно, что групповая скорость связана с законом дисперсии следующим соотношением . В одномерном случае соответственно имеем . При нулевой скорости закон дисперсии должен иметь экстремум (экстремумы).

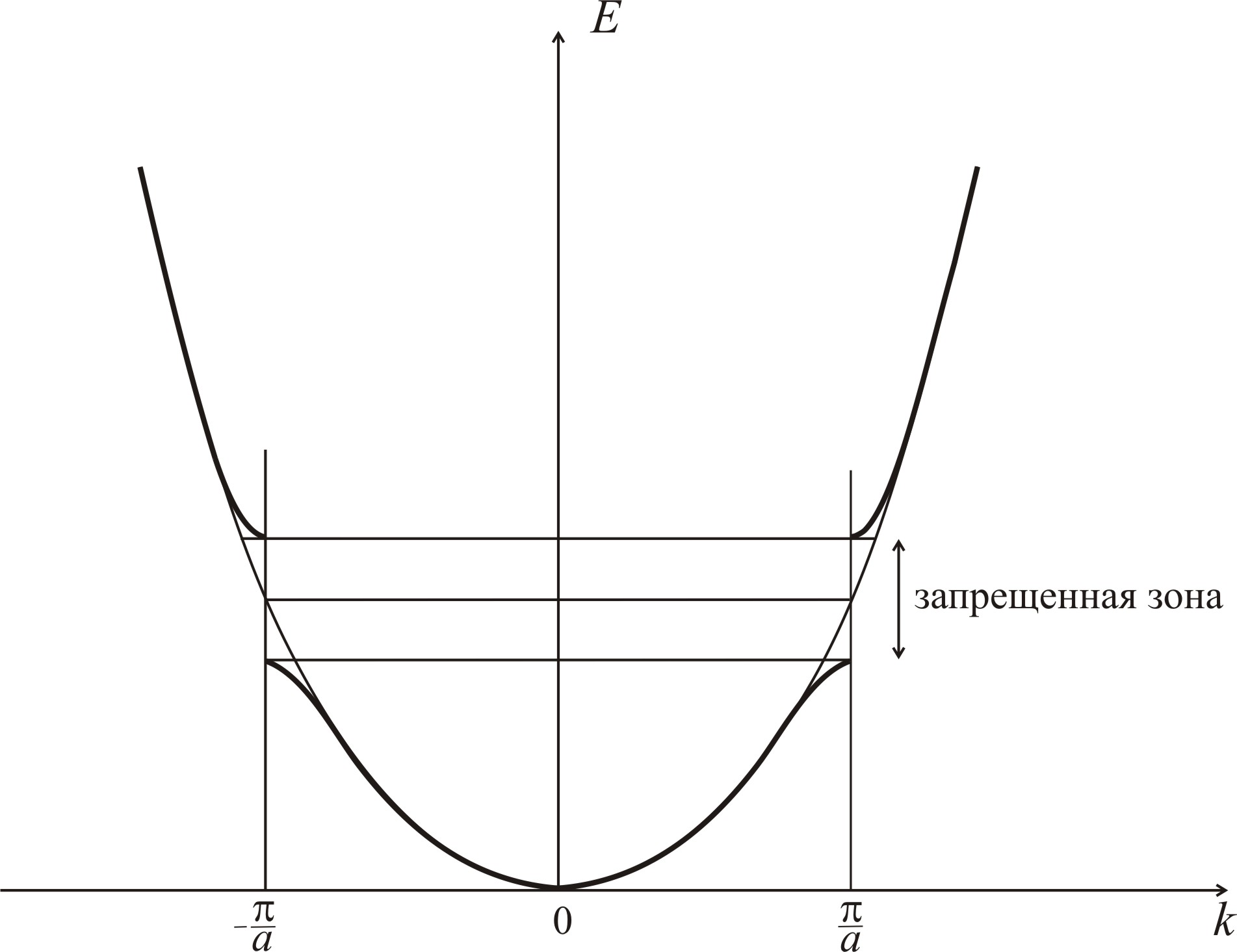
Рис. 5.2. Схема вскрытия запрещенной зоны энергии на границе 1-ой зоны Бриллюэна

Поэтому вблизи границ зон Бриллюэна закон дисперсии отклоняется от параболической зависимости , соответствующей состоянию свободной частицы, а на границах происходит разрыв зависимости и образование запрещённых зон (Рис. 5.2.).

5.3. Классификация кристаллов на диэлектрики, полупроводники и металлы

Два основных метода зонной теории, методы сильной и слабой связи, исходя из альтернативных приближений относительно связи электрона с атомами кристаллической решётки (сильная или слабая связь), дают единую картину чередующихся разрешённых и запрещённых зон энергии электрона, которая позволяет классифицировать кристаллы на металлы, диэлектрики и полупроводники.

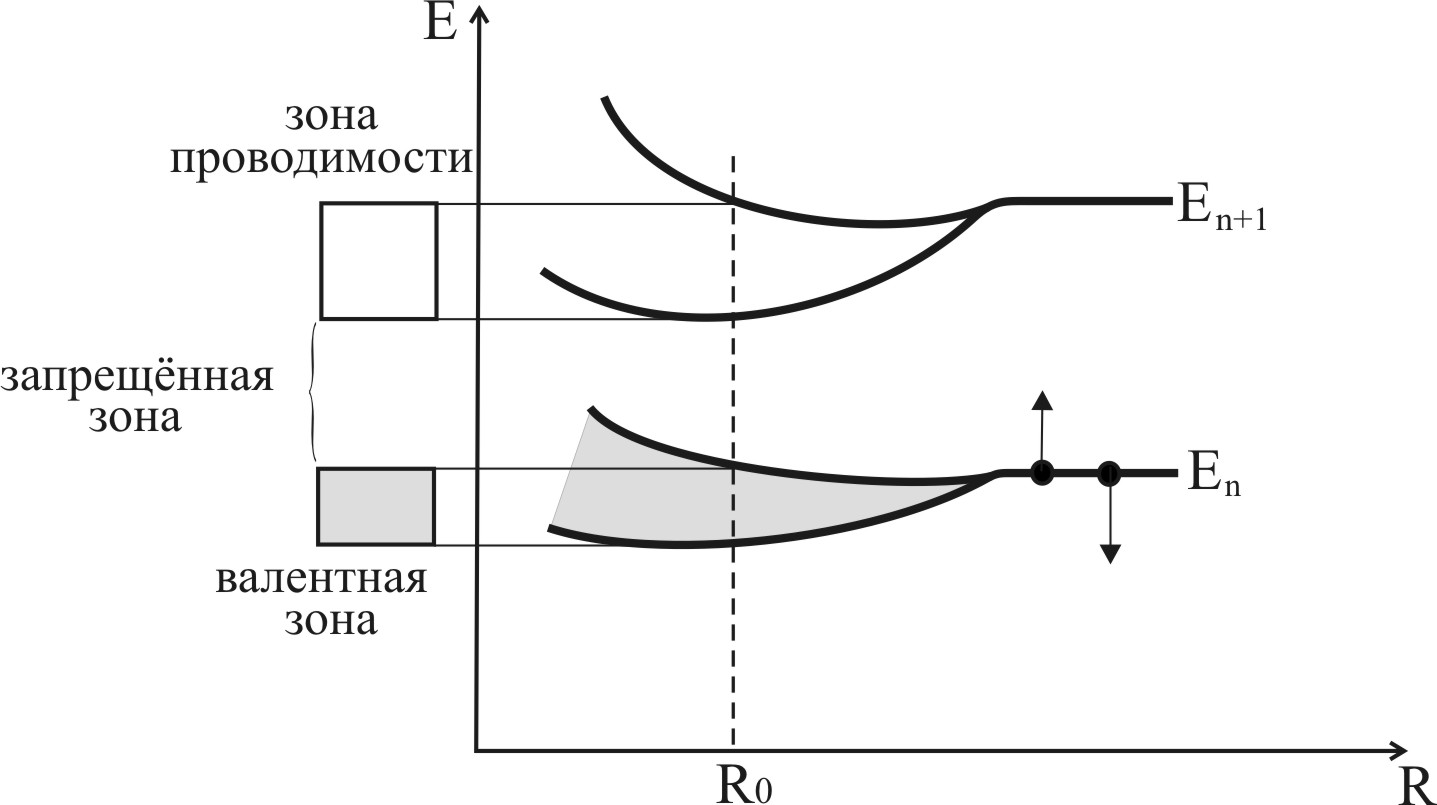
Рис. 5.3. Схема расщепления атомных уровней в разрешённые зоны энергии электрона при конденсации газа в кристалл

При сближении атомов в ходе конденсации незаполненный атомный уровень расщепится в незаполненную (пустую) разрешённую зону. Уровень, заполненный внешними электронами атома, расщепится соответственно в заполненную разрешённую зону, называемую валентной. Пустая зона, расположенная над валентной, называется зоной проводимости. Эти зоны отделены запрещённой зоной. Такая зонная картина соответствует диэлектрикам и полупроводникам.

Если ширина запрещённой зоны превышает энергию светового фотона ( 2-3 эВ), то свет не поглощается кристаллом, соответственно в кристалле не образуются свободные носители заряда (электроны в зоне проводимости и дырки в валентной зоне), поэтому такой кристалл является диэлектриком. Если ширина запрещённой зоны 2 эВ, то кристалл является полупроводником, так как он проводит электрический ток при освещении за счёт внутреннего фотоэффекта и его электропроводность экспоненциально растёт с ростом температуры, поскольку концентрация свободных носителей заряда возрастает с температурой по закону Аррениуса , определяющий вероятность преодолевания энергетического барьера (ширины запрещённой зоны) при температуре Т за счёт термических флуктуаций.

Наконец, не полностью заполненный атомный уровень расщепится в частично заполненную электронами разрешённую зону. Такие зоны, также называемые зонами проводимости, образуются при расщеплении частично (наполовину) заполненного атомного уровня, а также при наложении зон (образование гибридных зон) при расщеплении близко расположенных атомных уровней. Частично заполненные зоны характерны для металлов. При абсолютном нуле электроны заполняют в соответствии с принципом Паули уровни в зоне проводимости вплоть до некоторой граничной энергии, называемой энергией Ферми E_f. Уровень Ферми отделяет область заполненных уровней от незаполненных. Под действием внешнего электрического поля электроны металла могут легко переходить на незанятые уровни, увеличивая свою энергию, т.е. проводить электрический ток. Таким образом, зонная теория позволяет классифицировать кристаллы по проводимости на металлы, полупроводники и диэлектрики.