- •Содержание
- •Введение
- •Глава 1. Трансляционная симметрия кристалла
- •Глава 2. Колебания атомов кристаллической решётки
- •2.1. Гармоническое приближение
- •2.2. Колебания атомов одномерного кристалла с одним атомом в элементарной ячейке
- •2.3. Колебания одномерного кристалла с двумя атомами в элементарной ячейке
- •2.4. Колебания атомов в трехмерном кристалле
- •Глава 3. Квантовая теория тЕплоёмкосТи кристалла
- •3.1. Модель Дебая
- •3.2. Плотность состояний фононного спектра
- •3.3. Циклические граничные условия Борна-Кармана
- •3.4. Интерполяционная формула Дебая
- •3.5. Законы Дебая и Дюлонга-Пти
- •3.6. Физический смысл температуры Дебая
- •Глава 4. ЭлЕктронные состояния в кристалле
- •4.1.Теорема Блоха
- •4.2. Понятие квазиимпульса
- •4.3. Обратная решётка
- •4.4. Неоднозначность квазиимпульса
- •4.5. Приведение к первой зоне Бриллюэна
- •4.6. Количество состояний в зоне Бриллюэна
- •Глава 5. Элементы зонной теории кристаллов
- •5.1. Метод сильносвязанных электронов
- •5.1.1 Метод сильной связи без учёта симметрии кристалла
- •5.1.2. Метод сильной связи с учётом симметрии кристалла
- •5.2. Метод слабосвязанных электронов
- •5.3. Классификация кристаллов на диэлектрики, полупроводники и металлы
- •Глава 6. Электронная теория металлов
- •6.1. Основные недостатки классической теории металлов.
- •6.2. Уровень Ферми. Поверхность Ферми
- •6.3. Температура Ферми. Критерий вырождения ферми-газа
- •6.4. Электронная теплоёмкость металла
- •6.5. Электрон-фононное взаимодействие и электропроводность металлов
- •6.5.1. Квазиклассические уравнения движения электрона в кристалле.
- •6.5.2. Физический смысл длины свободного пробега электрона
- •6.5.3. Электропроводность нормальных металлов при высоких
- •6.6. Сверхпроводимость
- •Глава 7. Полупроводники
- •7.1. Носители заряда в полупроводниках
- •7.1.1. Законы дисперсии электронов и дырок
- •7.1.2. Статистика носителей заряда в полупроводниках
- •7.1.3. Равновесная концентрация электронов и дырок
- •7.2. Проводимость собственных полупроводников
- •7.3. Проводимость легированных полупроводников
- •7.3.1. Элементарная теория мелких центров
- •7.3.2. Электропроводность легированных полупроводников
- •Глава 8. Методы исследования электронной структуры металлов и полупроводников
- •8.1. Гальваномагнитные методы и циклотронный резонанс
- •8.1.1. Эффект Холла
- •8.1.2. Движение электрона в магнитном поле
- •8.1.3. Циклотронный резонанс в металлах
- •8.2. Квантование энергии электрона в магнитном поле. Уровни Ландау
- •8.3. Квантовые осцилляционные эффекты
- •Литература
- •392008, Г. Тамбов, ул. Советская, 190г
5.1.2. Метод сильной связи с учётом симметрии кристалла
Рассмотрим
одномерный одноатомный кристалл, т.е.
с одним атомом в элементарной ячейке.
Положения атомных ядер в одном кристалле
определяется вектором решётки Rl=la,
где а
– межатомное расстояние, l=1,2…Nат.
Волновая функция электрона определяется
относительным расстоянием между
электроном и ядром
![]() .
Из теоремы Блоха следует, что
.
Из теоремы Блоха следует, что
![]() , (8)
, (8)
где k – квазиволновой вектор электрона, откуда
![]() . (9)
. (9)
В общем случае состояние электрона в кристалле определяется суммой блоховских состояний
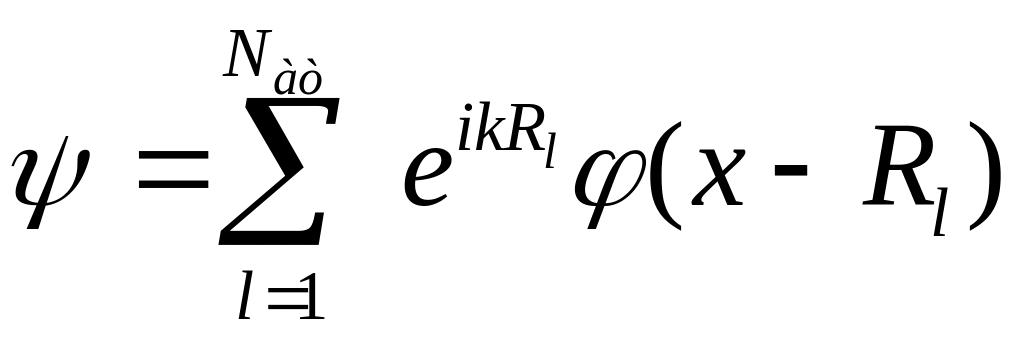 .
(10)
.
(10)
Сумма (10) представляет
разложение (4) с учётом теоремы Блоха.
Атомными орбиталями являются функции
![]() а коэффициентами разложения сl
являются множители вида
а коэффициентами разложения сl
являются множители вида
![]() .
.
Для того, чтобы использовать решения предыдущего параграфа вычислим сначала в выражении ( ) правую часть
![]()
Перепишем ( ) в виде:
![]() .
(11)
.
(11)
В сумме в правой
части этого уравнения выделим слагаемое
с
![]() :
:
![]() . (12)
. (12)
Диагональные
матричные элементы оператора возмущения
![]() есть среднее значение потенциальной
энергии взаимодействия электрона с
полем соседних атомов. В
методе сильной связи учитывается влияние
только ближайших соседей.
Так как в кристалле расстояние между
соседними атомами одинаково, то эта
средняя энергия не зависит от номера
атома
есть среднее значение потенциальной
энергии взаимодействия электрона с
полем соседних атомов. В
методе сильной связи учитывается влияние
только ближайших соседей.
Так как в кристалле расстояние между
соседними атомами одинаково, то эта
средняя энергия не зависит от номера
атома
![]() ,
т.е.
,
т.е.
![]() .
Поэтому расщепление уровня
.
Поэтому расщепление уровня
![]() в разрешённую зону при сближении атомов
будет полностью определяться
недиагональными матричными элементами
оператора возмущения
в разрешённую зону при сближении атомов
будет полностью определяться
недиагональными матричными элементами
оператора возмущения
![]() ,
которые в одномерном случае имеют вид
,
которые в одномерном случае имеют вид
![]()
![]() .
.
В приближении
ближайших соседей
![]() ,
а отличными от нуля матричными элементами
принимаются
,
а отличными от нуля матричными элементами
принимаются
![]() ,
которые зависят только от расстояния
между ближайшими соседями, т.е. от
межатомного расстояния, а
,
которые зависят только от расстояния
между ближайшими соседями, т.е. от
межатомного расстояния, а
![]() и поэтому не зависят от номера l.
С учётом этих приближений выражение
для уровня энергии электрона в кристалле
принимает вид
и поэтому не зависят от номера l.
С учётом этих приближений выражение
для уровня энергии электрона в кристалле
принимает вид
![]() .
(13)
.
(13)
В одномерном случае
и приближении ближайших соседей сумма
в правой части (13) состоит из двух
слагаемых:
![]() .
Поэтому зависимость энергии электрона
от квазиволнового вектора, т.е. закон
дисперсии зонного электрона,
принимает вид
.
Поэтому зависимость энергии электрона
от квазиволнового вектора, т.е. закон
дисперсии зонного электрона,
принимает вид
![]() .
(14)
.
(14)
Таким образом, под
действием возмущения со стороны ближайших
соседних атомов по решётке атомный
уровень
смещается на величину
![]() и расщепляется в зону шириной 4V(a),
определяемой недиагональными матричными
элементами оператора межатомного
взаимодействия
и расщепляется в зону шириной 4V(a),
определяемой недиагональными матричными
элементами оператора межатомного
взаимодействия
![]() .
Взаимодействие электрона с ионами
кристаллической решётки носит характер
притяжения, поэтому
<0
и V(a)<0.
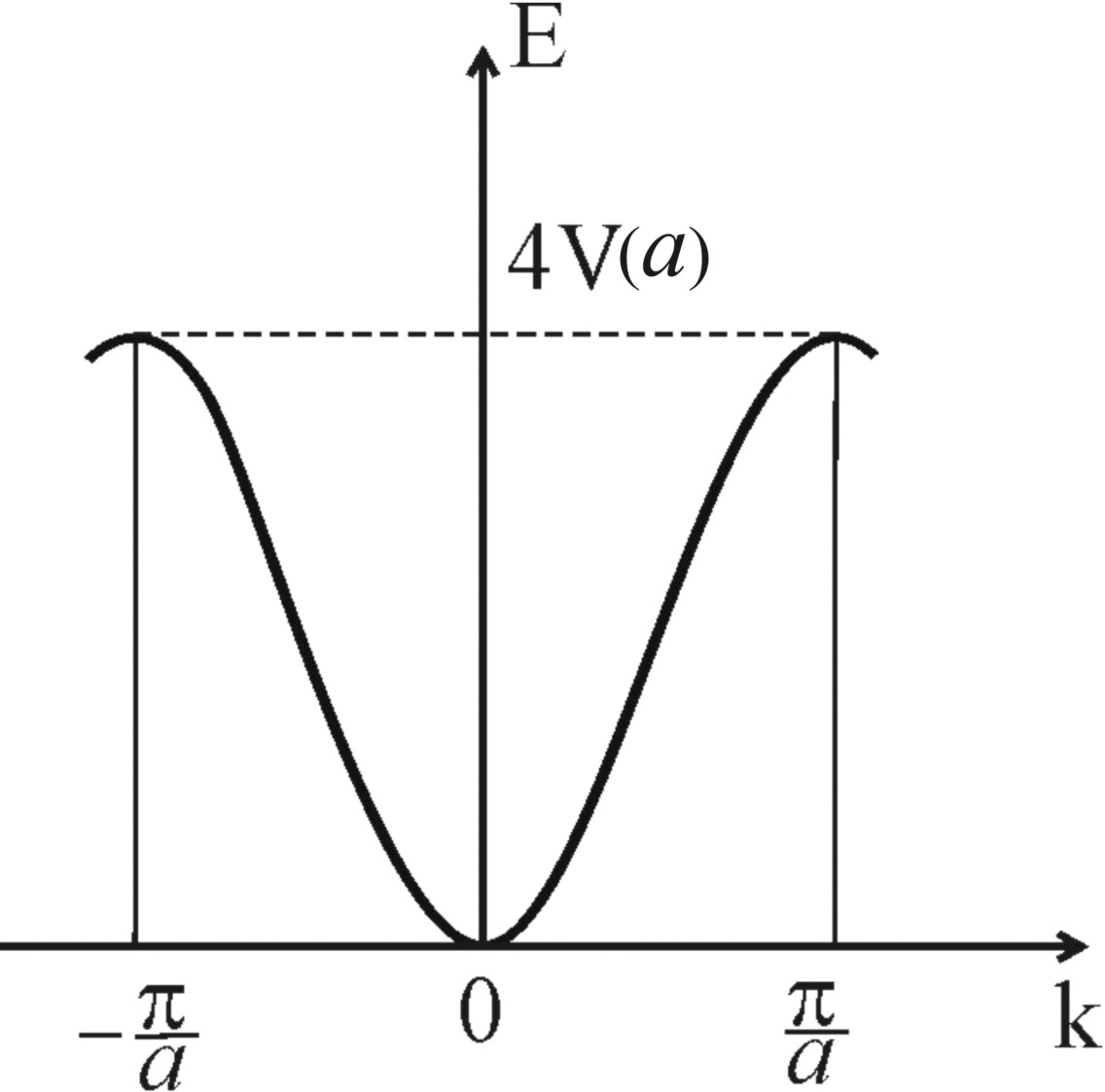
На рис. 5.1. показана зависимость E(k),
отсчитанная от минимального значения
энергии в первой зоне Бриллюэна.
.
Взаимодействие электрона с ионами
кристаллической решётки носит характер
притяжения, поэтому
<0
и V(a)<0.
На рис. 5.1. показана зависимость E(k),
отсчитанная от минимального значения
энергии в первой зоне Бриллюэна.
|
Рис. 5.1. Закон дисперсии зонного электрона в методе сильной связи |
Для кристалла
конечных размеров k-ось
дискретна: на одно квантовое состояние
приходится отрезок, равный
,
где
![]() –
размер кристалла вдоль оси
–
размер кристалла вдоль оси
![]() .
Все физически различные состояния
находятся в первой зоне Бриллюэна, т.е.
в интервале значений квазиволнового
вектора от
.
Все физически различные состояния
находятся в первой зоне Бриллюэна, т.е.
в интервале значений квазиволнового
вектора от
![]() до
до
![]() .
Количество таких состояний равно числу
элементарных ячеек кристалла Nяч
(см. § 4.6.). Из-за симметрии закона дисперсии
относительно центра зоны Бриллюэна
E(k)=
E(-k),
каждый уровень энергии в зоне одномерного
кристалла двукратно вырожден и
следовательно число уровней в зоне
вдвое меньше, т.е. Nяч/2.
.
Количество таких состояний равно числу
элементарных ячеек кристалла Nяч
(см. § 4.6.). Из-за симметрии закона дисперсии
относительно центра зоны Бриллюэна
E(k)=
E(-k),
каждый уровень энергии в зоне одномерного
кристалла двукратно вырожден и
следовательно число уровней в зоне
вдвое меньше, т.е. Nяч/2.